こんにちは!ケンけんです。
今回は、剰余体$M \otimes _{A} \kappa(\mathfrak{p}) \cong M_{\mathfrak{p}}/\mathfrak{p}M_{\mathfrak{p}}$と言う同型変形が松村先生の「可換環論」で自明のように書かれて詰まったため、解決するまでの必要な性質をまとめます。
それでは行ってみよう!
キーワード:剰余体
必要知識:加群のテンソル積と局所化
この記事では、環はすべて単位的可換環とします。
tensor product
まずテンソル積の普遍性(定義)を再確認しておきます。
$R$を環とし, $M,N,P$を$R$加群とする.
$F:L \times M \rightarrow N$を$R$双線形写像とする.
つまり, 次を満たす.
$F(ax+by,cz+dw)=acF(x,z)+bcF(y,z)+adF(x,w)+bcF(y,w)$
$(a,b,c,d \in R, x,y \in M,z,w \in N)$
このとき, $R$加群$T$と$R$双線形写像$\otimes :M \times N \rightarrow T$の組$(T, \otimes )$が存在し次の図式を可換にする$\widetilde{F}:T \rightarrow P$が一意的に存在する.
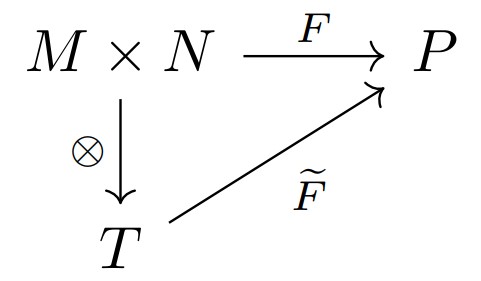
同型を除き一意的に$T$が決まるため, $T=M \otimes _{R} N$と書き, $M,N$のテンソル積と呼ぶ.
($\widetilde{F}$は$m \otimes n \in M \otimes _{R} N$について$\widetilde{F}(m \otimes n)=F(m,n)$となっている.)
この命題は、テンソル積の定義であり一意的な存在を示す普遍性と呼ばれるものです。
ちなみに、$T$は構成上商集合で$\widetilde{F}$は誘導された写像になります。(参考)
また、テンソル積は次のように同型が成り立ちます。
$R$を環とし, $M,N, P$を$R$加群とする.
$(1)$ $M \otimes_{R}N \cong N \otimes_{R} M$
$(2)$ $(M \otimes_{R} N) \otimes_{R} P \cong M \otimes_{R}(N \otimes_{R} P)$
$(3)$ $(M \oplus N ) \otimes_{R} P \cong (M \otimes_{R} P) \oplus (N \otimes_{R} P)$
$(4)$ $R \otimes_{R} M \cong M$
同型を通して乗法と同じ操作ができるということです。今回は、特に$(2)$を使用します。
定義とこの命題の証明は、結構面倒なのでこの記事では取り扱いません。
今回はこれらの性質と次の節で示す事実を元に、主題の同型を示します。
剰余加群と局所化の表示
それでは剰余加群と局所化をテンソル積で表現できることを示していきます。
$R$を環とし, そのイデアルを$I$, 積閉集合を$S$, $M$を$R$加群を取る.
$(1)$ $M/IM \cong M \otimes_{R} R/I$
$(2)$ $M_{S} \cong M \otimes_{R} R_{S}$
分量が増えるため、写像のwell-defined等はテンソル積の性質を使うモノを除き省略しました。
$F:M \times R/I \rightarrow M/IM((m,\overline{a}) \mapsto \overline{am})$は$R$双線形写像である.
従って, $R$線形写像$\widetilde{F}:M \otimes_{R} R/I \rightarrow M/IM(m \otimes \overline{a} \mapsto \overline{am})$を一意的に誘導する.
次に$G:M/IM \rightarrow M \otimes_{R} R/I(\overline{m} \mapsto m \otimes \overline{1})$を定義する.
$\overline{m}=\overline{m’} \in M/IM$を取ると, $m-m’=in(i \in I, n \in M)$である.
$\overline{i}=\overline{0}$とテンソル積の双線形性より次の変形が成り立つ.
$m \otimes \overline{1}=(in+m’) \otimes \overline{1}=in \otimes \overline{1}+m’ \otimes \overline{1}=n \otimes \overline{i}+m’ \otimes \overline{1}=m’ \otimes \overline{1}$.
従って, $G$はwell-definedである. ($R$線形性は明らか)
$\overline{m} \in M/IM$について$(\widetilde{F} \circ G)(\overline{m})=F(m \otimes \overline{1})=\overline{m}$である.
また, $m \otimes \overline{a} \in M \otimes_{R} R/I$について
$(G \circ \widetilde{F})(m \otimes \overline{a})=G(\overline{am})am \otimes \overline{1}=m \otimes \overline{a}$である.
以上から, $G=\widetilde{F}^{-1}$となり$M/IM \cong M \otimes_{R} R/I$である.
$F:M \times R_{S} \rightarrow M_{S}((m,a/s) \mapsto am/s)$は$R$双線形写像である.
従って, $R$線形写像$\widetilde{F}:M \otimes_{R} R_{S} \rightarrow M_{S}(m \otimes a/s \mapsto am/s)$を一意的に誘導する.
次に$G:M_{S} \rightarrow M \otimes_{R} R_{S}(m/s \mapsto m \otimes 1/s)$を定義する.
$m/s=m’/s’ \in M_{S}$を取ると, ある$v \in S$により$v(s’m-sm’)=0$を満たす.
$vs’m=vsm’$とテンソル積の双線形性より次の変形が成り立つ.
$m \otimes 1/s=m \otimes vs’/vss’=vs’m \otimes 1/vss’=vsm’ \otimes 1/vss’=m’ \otimes 1/s’$.
従って, $G$はwell-definedである.($R$線形性は明らか)
$m/s \in M_{S}$に対し, $(\widetilde{F} \circ G)(m/s)=\widetilde{F}(m \otimes 1/s)=m/s$である.
また$m \otimes a/s \in M \otimes_{R} R_{S}$に対し,
$(G \circ \widetilde{F})(m \otimes a/s)=g(am/s)=am \otimes 1/s=m \otimes a/s$である.
以上から, $G=\widetilde{F}^{-1}$であり$M_{S} \cong M \otimes_{R}R/I$である.
$\square$
このように、加群の様々な操作はテンソル積で表現できます。
(ネーター環上の有限生成加群の場合は完備化もテンソル積で表現できます。)
これで必要な道具がそろったので本題の同型を示していきます。
テンソル積の書き換え
$R$を環とし, $\mathfrak{p}$をその素イデアル, $M$を$R$加群とする.
また, $\mathfrak{p}$の剰余体を$\kappa(\mathfrak{p})=R_{\mathfrak{p}}/\mathfrak{p}R_{\mathfrak{p}}$とする.
このとき次が成り立つ.
- $M \otimes_{R}\kappa(\mathfrak{p}) \cong M_{\mathfrak{p}}/\mathfrak{p}M_{\mathfrak{p}}$
$R_{\mathfrak{p}}$を$R$加群とみなすと, 命題2から$\kappa(\mathfrak{p}) \cong R_{\mathfrak{p}} \otimes_{R} R/\mathfrak{p}$である.
従って, $R$加群として命題1を利用すると次の変形ができる.
$M \otimes_{R} \kappa(\mathfrak{p}) \cong M \otimes_{R} (R_{\mathfrak{p}} \otimes_{R} R/\mathfrak{p}) \cong (M \otimes_{R} R_{\mathfrak{p}}) \otimes_{R} R/\mathfrak{p}$.
命題2を用いることで$M \otimes_{R} R_{\mathfrak{p}} \cong M_{\mathfrak{p}}$, $M_{\mathfrak{p}} \otimes_{R} R/\mathfrak{p} \cong M_{\mathfrak{p}}/\mathfrak{p}M_{\mathfrak{p}}$が成り立つ.
以上から, $M \otimes_{R}\kappa(\mathfrak{p}) \cong M_{\mathfrak{p}}/\mathfrak{p}M_{\mathfrak{p}}$である.
$\square$
おわりに
ちなみに動機となった書籍では、このぐらいの変形は自明らしく一行で同型変形しています。
今回はまだ単純な道具だけでよかったのですが、これがすぐに埋められないタイプの行間だと解消に恐ろしく時間がかかることになる。数学書の恐ろしさを改めて感じました。
以上、ケンけんでした。
参考文献
動機となった書籍
松村英之, 可換環論, 共立出版