こんにちは!ケンけんです。
前回は、同値類と商集合を考え集合を同値関係で分けることを取り扱いました。
今回は、「自然な射影」と「誘導写像」を取り扱います。
そして、商集合を取る意味である「全単射の構成」も考えます。
キーワード:自然な射影と誘導写像
定義 自然な射影と誘導写像
今回は、商集合自体を考えるため具体例からの導入なく議論を始めます。
まず、写像$f:X \rightarrow Y$(全射や単射か不明)に対して$X$の同値関係$\sim$に次の条件を仮定します。
$$x \sim y \Rightarrow f(x)=f(y)$$
注意ですが、これは$\sim$の定義ではなく「同値($\sim$)ならば、像が一致する」命題です。
そして、次の2つの写像?を考えます。
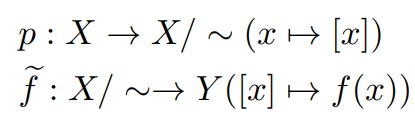
この2つは写像のようですが、商集合の元は「代表元」の取り方で変わります。
そのため、代表元の取り方に依存しないこと(well-defined)を調べる必要があります。
$p$について
$x,y \in X$について$x=y$を仮定すると,反射律より$x \sim x=y$である.
従って, $x \sim y$から$z \in [y]$について$z \sim x$である.
よって, $z \in [x]$となり$[y] \subset [x]$である.
逆の包含は同様に示され$[x]=[y]$となり$p(x)=p(y)$である.
以上から, $p$はwell-definedである.
$\widetilde{f}$について
$[x],[y] \in X/\sim $について$[x]=[y]$を仮定すると, $x \sim y$である.
従って, $f(x)=f(y)$であるため$\widetilde{f}([x])=\widetilde{f}([y])$となりwell-definedである.
$\square$
この2つの写像は、$p$が「自然な射影」、$\widetilde{f}$が「$f$から誘導される写像」と呼ばれます。
(証明を見るとわかりますが、$p$の方では「$\sim$」の仮定は使っていません。)
この2つの写像は、一緒に考えることが多く$f$の値域の別の表現にしたいときに用いられます。
主題となる命題を考える前にしっかり定義しておきます。
$X,Y$:集合 $f:X \rightarrow Y$:写像 $\sim$:$X$の同値関係
$\rm{(1)}$ $p:X \rightarrow X/\sim(x \mapsto [x])$:自然な射影($\rm{natural \; projection}$)
以下の同値関係$\sim$について次の命題を仮定する.
$$x \sim y \Rightarrow f(x)=f(y)$$
$\rm{(2)}$ $\widetilde{f}:X/\sim \rightarrow Y([x] \mapsto f(x))$:$f$から誘導される写像($\rm{induced \; map}$)
(以降は誘導写像と呼びます。)
先の$\sim$の仮定は、$\widetilde{f}$をwell-definedにするためのものです。
次の節では、この2つの写像から得られる情報を示していきます。
写像から全単射を作る
今回定義した2つの特別な写像は、像集合と全単射な商集合を作ることにあります。
その特徴を表すものが次の命題です。
$X,Y$を集合として, $f:X \rightarrow Y$を写像,$\sim$を$X$の同値関係とする.
このとき, 次が成り立つ.
$\rm{(1)}$ 自然な射影$p:X \rightarrow X/\sim$は全射である.
以下, $X$の同値関係$\sim$に次の仮定をする.
$$x \sim y \Rightarrow f(x)=f(y)$$
$\rm{(2)}$ $f$から誘導される写像$\widetilde{f}$で$f=\widetilde{f} \circ p$を満たすものは一意的に存在する.
つまり, 次の図式が可換である.
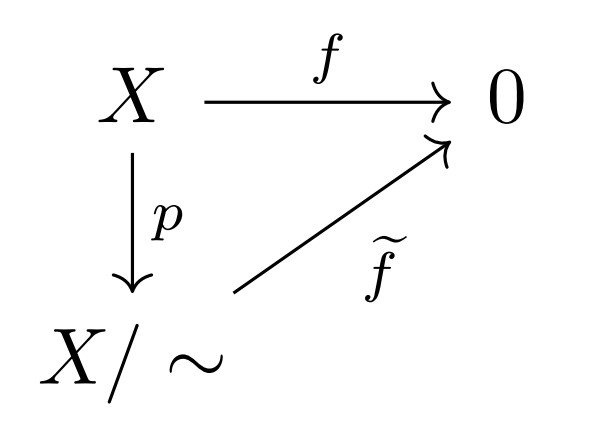
$\rm{(3)}$ $f$が全射である $\Rightarrow \widetilde{f}$は全射である,
$\rm{(4)}$ 「$x \sim y \iff f(x)=f(y)$」 $\Rightarrow \widetilde{f}$は単射である.
$\rm{(1)}$について
各$[x] \in X/\sim$をとると, $x \in X$より$p(x)=[x]$である.
従って, $p$ は全射である.
$\rm{(2)}$について
各$x \in X$に対して$f(x)=(\widetilde{f} \circ p)(x)$となることを示せば十分である.
$(\widetilde{f} \circ p)(x)=\widetilde{f}(p(x))=\widetilde{f}([x])=f(x)$である.
また, $F \circ p=f$とする$F:X/\sim \rightarrow Y$を取る.
このとき, 各$[x] \in X/\sim$に対して次のように$\widetilde{f}=F$が示される.
$\widetilde{f}([x])=(\widetilde{f} \circ p)(x)=f(x)=(F \circ p)(x)=F([x])$.
$\rm{(3)}$について
$f$の全射性から, 各$y \in Y$についてある$x \in X$で$y=f(x)$となる.
$\rm{(2)}$から, $y=f(x)=(\widetilde{f} \circ p)(x)=\widetilde{f}([x])$であるため$\widetilde{f}$は全射である.
$\rm{(4)}$について
各$[x],[y] \in X/\sim$について, $f(x)=f(y) \Rightarrow [x]=[y]$を示せば十分である.
$\sim$の仮定と$f(x)=f(y)$より, $x \sim y$である.
従って, $[x]=[y]$である.
$\square$
この命題(特に$\rm{(3),(4)}$)は、次のように全単射を必ず構成できます。
$X,Y$を集合として, $f:X \rightarrow Y$を写像,$\sim$を次のような$X$の同値関係とする.
$$x \sim y \iff f(x)=f(y)$$
このとき, 次のことが成り立つ.
- $(X/\sim) \cong f(X)$
- 特に, $f$が全射のとき$(X/\sim) \cong Y$である.
従って、値域$Y$について見たいときは整理された商集合$X/\sim$を調べてもわかります。
集合の同型(全単射を持つこと)は、調べたい集合を別の単純な集合に対応させて良いことでした。
上の商集合を取る操作はその一つで、演算も考えたものが「準同型定理」と呼ばれるものです。
今回の系に名前はありませんが、さしずめ「集合の同型定理」でいいのではないでしょうか。
なぜ$\widetilde{f}$が単射になるのか
ところで、なぜ$\sim$の仮定で$\widetilde{f}$は単射になるのでしょう。
それは、単射の定義を考えればわかります。
写像$f:X \rightarrow Y$について、$x,y \in X$を取り$f(x)=f(y)$を仮定します。
$f$が単射でない場合は、$x \neq y$があり得ます。
$\rm{(4)}$の仮定は、「$\sim$が$f$の像が一致する元で類別されている」ことを意味します。
なので$X/\sim$の代表系$X’$で制限写像$f|_{X’}$を考えると単射になります。
しかし、「代表系」では取り方がいくらでも存在するので集合の表現としてははっきりしません。
そこで、代表元に依存しない商集合から伸ばせるように自然な射影と誘導写像を使います。
「$x \sim y$」は「$[x]=[y]$」と同値です。
そうすると、単射の定義が成り立つようになります。
$$f(x) = f(y)\iff x \sim y \iff [x] = [y]$$
元の一致「$=$」より、少し緩い同値関係の「$\sim$」にすることで単射にできました。
商集合を利用するのは、元の取り方でwell-definedを崩れないようにするためだったのです。
おわりに
集合の同型定理を知っておくと、正直代数学の準同型定理はほぼほぼ明らかだとわかります。
演算を含めて考える代わりに、同値関係$\sim$の定義が命題の仮定そのものに変わります。
今後、この商集合と像集合の同型を考えるたびにここに戻ってくるでしょう。
次回は、「自然な射影」の逆である「断面」を取り扱います。
以上、ケンけんでした。
参考文献
今回の話を筆者が吸収する動機になった本(いい本だから読んでほしい)
横田一郎, 群と位相, 裳華房