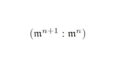こんにちは!ケンけんです。
商集合の元は同値類であり、すべて合わせると類別になっています。
今回は、同値類は類であることを示し、商集合で見る意義を考えます。
キーワード:完全代表系
同値類の類別
実は、同値類を定義した際に分割している前提で議論していました。
今回は「同値類は類なのか?」がメインです。
商集合の元である「同値類」は、元の集合の部分集合でした。
ここから、部分集合としての比較ができます。
しかし、同値類はこの比較が次のように二通りに絞られます。
$X$を集合とし, $\sim$を$X$上の同値関係,$a, b \in X$を取る.
また, 同値類を$[a]=X_{a}=\{x \in X|x \sim a\}$で表す.
同値類$X_{a},X_{b}$について次の2つは同値である.
(1)$X_{a}=X_{b}$
(2)$X_{a} \cap X_{b} \neq \emptyset$
(1) $\Rightarrow$(2)については$X_{a} \cap X_{b}$が$X_{a}$または$X_{b}$である.
同値類は空集合ではないため, (2)が成り立つ.
(2)$\Rightarrow$(1)について
(1)の否定「$X_{a} \neq X_{b}$」を仮定し, (2)を示せば十分である.
空集合の性質から, $X_{a} \cap X_{b} \subset \emptyset$だけを示す.
$X_{a} \cap X_{b} \neq \emptyset$を仮定し, $x \in X_{a} \cap X_{b}$を取る.
$x \sim a,x \sim b$と推移律から, $a \sim b$が成り立つ.
任意の$x \in X_{a},y \in X_{b}$について$x \sim a,y \sim b$である.
$a \sim b$から, $x \sim b,y \sim a$となり$X_{a}=X_{b}$が成り立つ.
これは仮定から矛盾であるため, $X_{a} \cap X_{b} = \emptyset$である.
以上から, $X_{a} \cap X_{b}=\emptyset$である.
$\square$
この性質は、異なる2つの同値類が部分集合として分けられていることを示しています。

以前、上の図のように脊椎動物の分類(同値類)が類別だとしれっといいました。
これは先の命題から本当なのだと分かります。
また一般の部分集合では、異なる部分集合どうしの比較基準がないためできません。
証明中の推移律のように、集合を比較する基準として「同値関係」は適しているのでした。
以上から、集合は同値類で類別できることがわかります。
$X$を集合とし, $\sim$を$X$上の同値関係とする.
また, $a \in X$の同値類を$[a]=X_{a}=\{x \in X|x \sim a\}$で表す.
このとき, $X= \bigcup_{s \in S}X_{s}$を満たす$S \subset X$が存在し類別である.
この$S$は類別の代表系である.
まず集合$X$に対して, $X=\bigcup_{x \in X}X_{x}$が成り立つ.
任意の$x,y \in X $に対して, $x \sim y$ならば$X_{x}=X_{y}$である.
従って, $S \subset X$を次のように同値な元が自分自身のみの集合として定義する.
$$\forall x, \forall y \in S(X_{x}=X_{y} \iff x=y) $$
$\bigcup_{s \in S}X_{s} \subset X$について
各$s \in S$に対し, $X_{s} \subset X$より$\bigcup_{s \in S}X_{s} \subset X$である.
$X\subset \bigcup_{s \in S}X_{s}$について
任意の$x \in X$に対し, $S$の構成から$x \sim t \in S$が存在する.
従って, $X \subset \bigcup_{s \in S}X_{s}$となる.
また命題NST-28′-1から, $X=\bigcup_{s \in S}X_{s}$は類別である.
$\square$
商集合の特徴づけ
先ほどの命題から、同値類により類別できることがわかりました。
そして、商集合についてもわかることがあります。
それは、商集合が任意の代表系と一対一対応(全単射)を持つことです。
$X$を集合とし, $\sim$を$X$上の同値関係,$a\in X$を取る.
また, 同値類を$[a]=X_{a}=\{x \in X|x \sim a\}$で表す.
このとき, $\sim$による任意の代表系$S$に対して$(X/\sim) \cong S$である.
直接示してもいいですが、今回は集合の準同型定理で楽に示します。
$f:X \rightarrow S$を次のように定義する.
$$f(x)=a(a \in S, x \sim a)$$
各$a \in S \subset X$について$f(a)=a$より$f$は全射である.
また, $x, y \in X$について次が成り立つ.
$$x \sim y \iff f(x)=f(y)$$
従って, 集合の準同型定理から$(X/\sim) \cong S$である.
$\square$
構成した$f$は、$S$の方で代表元が一つに固定されるため、像が取り変わりません。
従って、well-definedは確認不要です。
ちなみに代表系の定義を考えると、一般の類と代表系にも全単射は作れます。
証明中に構成した$f$をそのまま利用すれば、直接証明になりますがわかります。
同値類が、類であることから導かれる特徴づけでした。
おわりに
「同値類が類別であること」「商集合の表示」は高度な数学になるほど忘れられがちですが、具体例やイメージを持つ際に分割していることを覚えておくと可視化しやすくなります。覚えておいて損はないでしょう。
以上、ケンけんでした。