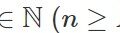こんにちは!ケンけんです。今回は、以前取り上げた短完全列の情報保存でわかる性質をより深く掘り下げようと言うものです。
それでは行ってみよう!
キーワード:短完全列の情報保存
exact sequence
さすがに定義はしつこいので短完全列の場合だけ触れます。
次の加群と線形写像の列$l$を取る.
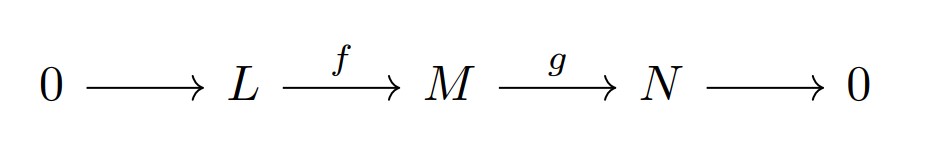
$\rm{(1)}$:$f$は単射, $g$は全射.
$\rm{(2)}$:$\mathrm{Ker}g=\mathrm{Im}f$
$\rm{(1),(2)}$をみたすとき, $l$は完全列であり短完全列と呼ぶ.
情報保存の利用例
さて、今回は短完全列の情報保存で他の有用な性質を導くことを考えます。
代表的なのは直和ですね。
$P$を$R$-加群の情報保存を満たす性質とする.
$\{M_{n}\}_{n =1, \ldots , m}$を$R$-加群の集合族とする.
このとき, 次が成り立つ.
$\{M_{n}\}$は$P$を満たす$ \iff \bigoplus _{n=1}^{m}M_{n}$は$P$を満たす.
$m$に関する帰納法で示す.
$m=2$のとき,
次の完全列を考える.

($i$は第1成分への包含写像, $p$は第2成分の射影)
$P$の情報保存より$M_{1},M_{2}$は$P$を満たすことと$M_{1} \oplus M_{2}$が$P$を満たすことは同値である.
$m \geq 2$のとき,
$M_{1}=\bigoplus _{n=1}^{m-1}M_{n}, M_{2}=M_{m}$とおくことで示される.
$\square$
つまり、以前わかったNoether加群やtorsion加群については有限個の直和でも保たれます。
各成分を調べて直接示すよりも単純ですね。
そして情報保存の強さは、「直和から各加群」への性質も保っている点です。
普通は、直和が条件を満たすと言って各加群がそうなるとは限りません。
情報保存が可能なら「加群単位」と「直和で全体」のどちらでも利用できる便利な性質となります。
また自明な完全列で剰余加群との関係もあります。
$P$を$R$-加群の情報保存を満たす性質とする.
$M$を$R$-加群とし, $N \subset M$をその部分加群とする.
このとき, 次が成り立つ.
$M$は$P$を満たす$ \iff N,M/N$は$P$を満たす.
次の自明な完全列を考える.
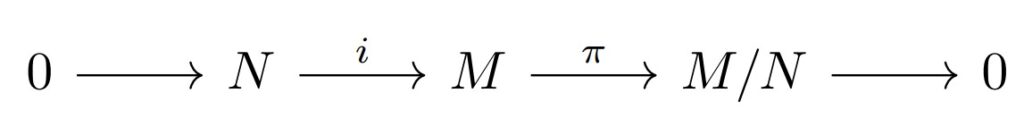
($i$は包含写像, $\pi$は自然な準同型)
$P$の性質から, $M$が$P$を満たすことと$N,M/N$が$P$を満たすことは同値である.
$\square$
この事実から、任意の加群$M$で$M/N$がNoether加群となるNoether部分加群$N$が存在するだけで元の$M$も自然とNoether加群となることがわかります。
特定のきれいな部分加群が見つけられるなら有用な性質になりそうです。
保存される情報 有限生成
現在Noether、Artin加群とtorsion加群については情報保存を満たしています。
今回は、少し特殊な環上で有限生成性も情報保存されることを示します。
$R$を$\rm{Noether}$加群として次の$R$-加群の完全列を取る.
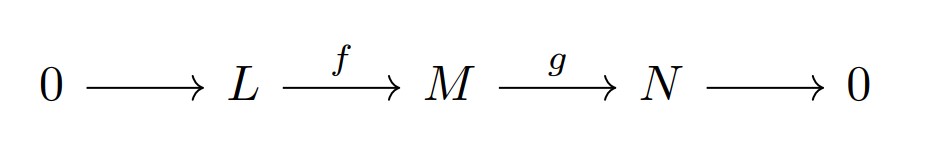
$M$は有限生成加群である $\iff L,N$は有限生成加群である.
$\Rightarrow$について
$M$を有限生成と仮定しその生成系を$\{m_{1}, \ldots , m_{n}\}$とする.
このとき, $M$はNoether加群であり, 部分加群$\mathrm{Ker}g$は有限生成である.
$f$は単射より準同型定理から$L \cong \mathrm{Ker}f$となる.
従って, $L$は有限生成である.
各$n \in N$に対し$g$の全射性より$n=g(m)(m=\sum_{i=1}^{n}r_{i}m_{i})$とする$m \in M$が存在する.
従って, $N$の元は$\{g(m_{1}), \ldots , g(m_{n})\}$を生成系とするため有限生成である.
$\Leftarrow$について
$L,N$を有限生成と仮定し, $\{l_{1}, \ldots , l_{p}\}$, $\{n_{1}, \ldots , n_{q}\}$をそれぞれの生成系とする.
各$m \in M$を取ると, $g(m)=\sum_{j=1}^{q}r_{j}n_{j}(r_{j} \in R)$と書ける.
$g$の全射性より各$j$で$g(a_{j})=n_{j}$とする$a_{j} \in M$が存在する.
$g(m)=g(\sum_{j=1}^{q}r_{j}a_{j})$より$m-\sum_{j=1}^{q}r_{j}a_{j} \in \mathrm{Ker}g=\mathrm{Im}f$である.
従って, ある$l=\sum_{i=1}^{p}s_{i}l_{i} \in L(s_{i} \in R)$によって$m-\sum_{j=1}^{q}r_{j}a_{j}=f(l)$と書ける.
従って, $m=\sum_{j=1}^{q}r_{j}a_{j}+\sum_{i=1}^{p}s_{i}f(l_{i})$と書ける.
以上から, $m$の元は$\{f(l_{1}), \ldots , f(l_{p}), a_{1}, \ldots , a_{q}\}$で生成されるため$M$は有限生成である.
$\square$
有限生成加群の生成系は一意的である必要はないので$N$の生成系の元の逆像を具体的に一つ選んでも問題ありません。
またNoether環の制限は、「Noether環上の有限生成加群はNoether加群」と「Noether加群の任意の部分加群は有限生成」の2つが必要なため要求しました。
なので、一般の環上では「$L,N \Rightarrow M$」のみ成り立ちます。
ここで今わかっている情報保存についてまとめておきます。
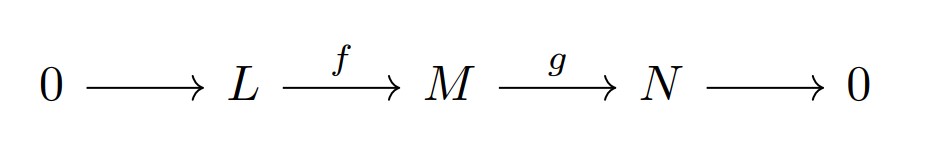
- $M$はtorison加群である $\iff L,N$はtorsion加群である,
- $M$はNoether(Artin)加群である $\iff L,N$はNoether(Artin)加群である,
- $L,N$はtorsion–free加群である $\Rightarrow M$はtorison–free加群である,
- $L,N$はdivisible加群である $\Rightarrow M$はdivisible加群である,
- $L,N$は有限生成である $\Rightarrow M$は有限生成である,
- $R$がNoether環の場合は, $L,N$は有限生成 $\iff M$は有限生成.
おわりに
情報保存を与えるだけでは意味がないので使い道を考えようの記事でした。
実際、私が初めて読んだNoether加群の直和は逆を考えていませんでしたが、今回書くにあたって逆も成り立つと言うことになりました。
また、最近Noether環上の有限生成加群や中山の補題等の有限生成加群の性質をよく利用するのでそれに咬ませた完全列の情報保存と追加で取り上げました。
以上、ケンけんでした。