 素朴集合論(NST)
素朴集合論(NST) NST-28’:きれいな類別として 同値類の類別
同値類の類別 様々な個所で利用される同値類は類の一種である。ここについて、詳しく議論になることが少なく高度な数学ではさも当たり前のようであるが、実際に確認しようとすると同値関係による整理だからうまく類別の性質を満たしていることがわかる。今回は、その確認と商集合についての言いかえにも触れる。
 素朴集合論(NST)
素朴集合論(NST) 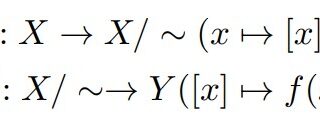 素朴集合論(NST)
素朴集合論(NST)  素朴集合論(NST)
素朴集合論(NST)  素朴集合論(NST)
素朴集合論(NST)  素朴集合論(NST)
素朴集合論(NST)  素朴集合論(NST)
素朴集合論(NST)  素朴集合論(NST)
素朴集合論(NST)