こんにちは!ケンけんです.
今回は,有限個のイデアルだからこそできる「素イデアル避け($\rm{prime \; avoidance}$)」を取り扱います.
キーワード:素イデアル避け
この記事では,環はすべて単位的可換環とします.
主張
今回はまず主張を示してそこから,意義を見てみましょう.
環$R$のイデアル$I,I_{i}(i=1,\ldots, n)$および素イデアル$P,P{j}(j=1,ldots, m)$を取る.
(1)$\bigcap_{i=1}^{n}I_{i} \subset P$ならば,ある$i$で$I_{i} \subset P$である.
(2)$I \subset \bigcap_{j=1}^{m}P_{j}$ならば,ある$j$で$I \subset P_{j}$となる.
(2)が素イデアル避け($\rm{prime \; avoidance}$)と呼ばれる技法になります.
証明が長いのでそれぞれに分割します.
(1)対偶「任意の$i$で$I_{i} \nsubseteq P$ならば,$\bigcap_{i=1}^{n}I_{i} \nsubseteq P$」を示す.
任意の$i=1,\ldots, n$に対し,$I_{i}\subsetneq P$を仮定する.
このとき,$x_{i} \in I_{i}\backslash P$が存在する.
素イデアルの定義から,
$x=x_{1}\cdots x_{n} \in \bigcap_{i=1}^{n}I_{i} \backslash P$が得られる.
従って,主張が成り立つ.
(2)対偶「任意の$j$で$I \nsubseteq P_{j}$ならば,$I\nsubseteq \bigcup_{j=1}^{m}P_{i}$である.」
を$m$に関する帰納法で示す.
$m=1$の時は明らかより,$m-1$まで主張を仮定する.
$j=1,\ldots, m$に関して$I\subsetneq P_{j}$を仮定する.
この時各$j$で$I \nsubseteq P_{j}$のため,
$m-1$までの仮定から$x_{j} \in I \backslash \cup_{k\neq j}P_{k}$が存在する.
任意の$j$で$x_{j} \notin P_{j}$ならば,
$I\backslash \bigcup_{j=1}^{m}P_{j}\neq \emptyset$から主張が成り立つ.
ある$j$で$x_{j} \in P_{j}$を仮定する.
$x_{\widehat{k}}=x_{1}\cdots x_{k-1}x_{k+1}\cdots x_{m}$に対し次の$x \in \bigcap_{k=1}^{m}I_{k}$を取る.
$$x=\sum_{k=1}^{m}x_{\widehat{k}}.$$
$k\neq j$に対し,$x_{k} \notin P_{i}$から$x_{\widehat{j}} \notin P_{j},x_{\widehat{k}} \in P_{j}$となる.
従って,$x \notin P_{j}$となり$x \in I \backslash \bigcup_{j=1}^{m}P_{j}$となる.
以上から,$I \nsubseteq \bigcup_{j=1}^{m}P_{j}$となる.
$\square$
横道ですが,実はBR1-12-1(1)の方はこちらの$\rm{Zariski}$閉集合の事実からも証明できます.
$\bigcap_{i=1}^{n}I_{i} \subset P$より,$P in \mathcal{V}(\bigcap_{i=1}^{n}I_{i})$である.
命題1(5)から,$\mathcal{V}(\bigcap_{i=1}^{n}I_{i})=\bigcup_{i=1}^{n}\mathcal{V}(I_{i})$となる.
従ってある$i=1,\ldots, n$で$P \in \mathcal{V}(I_{i})$であり,$I_{i} \subset P$となる.
$\square$
何がしたいのか?
これらの主張,特に後者の(2)は必要になるときに忘れて何度も見返す事態になります.
まずはこの主張の仮定部分の状況を考えてみます.
1.(1)の状況
(1)の状況は別証明にて登場した$\rm{Zariski}$閉集合に従うものになります.
例えば,イデアルの根基は素イデアルイデアルの共通部分で表示されます.
環$R$のイデアル$I \subset R$に対して,根基イデアル$\sqrt{I}$は次のように表示できます.
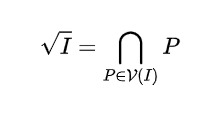
しかしこの場合では,$I \subset \sqrt{I}\subset P’ \in \mathrm{Spec}R$から$P’ \in \mathcal{V}(I)$です.
従って主張(1)は,かなり当たり前になります.
2.(2)の状況
それでは(2)の素イデアルの和集合の主張はどうでしょう.
イデアルの和集合はイデアルではないため,これまであまり考えてきませんでした.
ですが,こちらの方は非零因子の存在を保証する際に重要となります.
次の主張を示してみます.
環$R$の零因子全体の集合を$Z(R)$と$\Sigma=\{I \subset R|I \subset Z(R),I:\text{イデアル}\}$
(1)$\Sigma$は極大元を持つ.(つまり$\rm{Zorn}$の補題から極大元が存在する.)
(2)$\Sigma$の極大元は素イデアルである.
(3)$\mathcal{P}=\{P \in \mathrm{Spec}R|P \subset Z(R)\}$に対し,$Z(R)=\bigcup_{P \in \mathcal{P}}P$である.
(1)$S \subset \Sigma$を全順序部分集合とする.
極大イデアルの存在証明と同様に,$I=\bigcap_{J \in S}J$はイデアルであり$I \subset Z(R)$となる.
従って,$S$は$\Sigma$内で上界を持つため$\rm{Zorn}$の補題から極大元が存在する.
(2)$\Sigma$の極大元$P$を取り,$P \in \mathrm{Spec}R$を示す.
$x,y \notin P$を取ることで,$P \nsubseteq (x)+P,(y)+P$となる.
$P$は$\Sigma$の極大元より,$(x)+P,(y)+P$は非零因子をもつ.
よって,非零因子$ax+p \in (x)+P,by+q \in (y)+ P$が取れる.
$(ax+p)(by+q)=abxy+(axq+byp+pq) \in (xy) +P$は非零因子となる.
よって$P \subsetneq (xy)+P$となるため,$xy \notin P$となる.
以上から$P \in \mathrm{Spec}R$となる.
(3)$X=\bigcup_{P \in \mathcal{P}}P$とおく.
$X \subset Z(R)$は明らかなので,逆の包含を示す.
任意の零因子$x \in Z(R)$に対し,
問題から$(x) \subset P$となる極大元$P$が存在する.
(1)から$P \in \mathrm{Spec}R$より,$x \in X$となる.
以上から,$Z(R)=X$となる.
$\square$
この主張は[1]のExerciese1.14を細かく分解したものになります.
$\rm{Noether}$環の場合(先の話題のため流し読み推奨)
さて,$Z(R)$は素イデアルの和集合で表示できました.
一般には有限個とは限りませんが,重要な環の場合は必ず有限個になります.
それは$\rm{Noether}$環で,これはイデアルの増大列($\subset$で)が有限個となる環です.
主張はより一般には,$\rm{Noether}$環上の加群にまで拡張できます.
例えば,先ほどの零因子に関する命題が次のように置き換わります.
$\rm{Noether}$環$R$上の加群$M$に対し,次が成り立つ.
$$Z_{R}(M)=\bigcup_{P \in \mathrm{Ass}_{R}M}P.$$
$\mathrm{Ass}_{R}M$はまた$\mathrm{Spec}R$の部分集合でBR1-12-2でいう$\mathcal{P}$に相当します.
そして$\mathrm{Ass}_{R}M$は,$M$が有限生成ならば有限集合になることが知られています.
(いずれ取り上げます.)
このとき,次のような議論が可能になります.
- $\rm{Noether}$環$R$上の加群$M$およびイデアル$I$を取る.
- $Z_{R}(M)=\bigcup_{P \in \mathrm{Ass}_{R}M}P$(右辺は有限個の和集合)
- $I \subset Z_{R}(M)$ならば,素イデアル避けからある$P \in \mathrm{Ass}_{R}M$で$I \subset P$
この議論は今後イデアル$I$が($M$の)正則元を持つことを示すために背理法で利用されます.
直接非零因子が存在することを示すことは,抽象的な議論では難しいです.
しかしこの方法を用いることで,否定的証明ながらも存在を保証できます.
環論の高等な議論では$\rm{Noether}$性が現れますが,非零因子の話題も一つの重要な点です.
おわりに
久しぶりに記事を書いたので,少しぐだぐだになってしまったかもしれません.
$\rm{Noether}$環の項目はまだ紹介もしていない内容なので,認識しているだけで十分です.
素イデアル避けに,利用先があることを知るだけでもかなり有用だと思います.
以上,ケンけんでした.
参考文献
[1]M.F.Atiyah,I.G.Macdonald, Introduction to Commutative Algebra, Addkison-Wesley,Reading, MA,1969