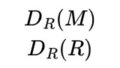こんにちは!ケンけんです。
今回は、加群版の誘導写像と準同型定理を扱います。
実質この記事を加群に拡張したものです。
キーワード:準同型定理
前提知識:誘導写像
この記事では、環はすべて単位的可換環とします。
今回の相手 準同型定理
まず、解決する相手を知りましょう。
$M,N$を$R$加群とし, $f:M \to N$を$R$線形写像とする.
$L$を$M$の部分加群とする.
(1)$L \subset \mathrm{Ker}f$ならば, $R$線形写像$\widetilde{f}:M/L \to N$が誘導される.
(2)$\widetilde{f}:M/\mathrm{Ker}f \to N$は単射である.
$M,N$を$R$加群とし, $f:M \to N$を$R$線形写像とする.
(1)$M/\mathrm{Ker}f \cong \mathrm{Im}f$.
(2)特に$f$が全射ならば, $M/\mathrm{Ker}f \cong N$.
書籍ごとで1-6-1なしで1-6-2をいきなり示していることもあります。
1-6-2からでは、「写像構成$\to$well-definedと線形性確認$\to$全単射確認」と煩わしいです。
ですが、先に挙げた記事(NST-28-2)から線形な誘導写像が構成できれば十分になります。
一意性は、誘導写像の構成から勝手に出てくるため不要ですし。
つまり、1-6-1(2)の方がずっと大切な性質になります。
(1)$x,y \in M$に対し, 「$x-y \in L \Rightarrow f(x)=f(y)$」を満たせば$\widetilde{f}$が定義できる.
$L \subset \mathrm{Ker}f$より$f(x-y)=0_{N}$のため$f(x)=f(y)$である.
従って, $\widetilde{f}:M/L \to N(\overline{x} \mapsto f(x))$がwell-definedである.
$\overline{x},\overline{y} \in M/L,r \in R$を任意で取る.
$\begin{align*}\widetilde{f}(\overline{x}+\overline{y})&=\widetilde{f}(\overline{x+y}) =f(x+y)\\ &=f(x)+f(y)\\ &= \widetilde{f}(\overline{x})+\widetilde{f}(\overline{y}).\end{align*}$
$\begin{align*}\widetilde{f}(r\overline{x})&=\widetilde{f}(\overline{rx}) =f(rx)\\ &=rf(x)\\ &= r\widetilde{f}(\overline{x}).\end{align*}$
以上から, $\widetilde{f}$は$R$線形写像である.
(2)$\widetilde{f}$の単射性は,「$x-y \in \mathrm{Ker}f \iff f(x)=f(y)$」を示せば十分である.
特に$\Leftarrow$を確認する.
任意の$x,y \in \mathrm{Ker}f$に対し, $f(x)=f(y)$を仮定する.
$f(x-y)=0_{N}$から, $x-y \in \mathrm{Ker}f$が得られる.
$\square$
(1)MOD1-4-1から単射$R$線形写像$\widetilde{f}:M/\mathrm{Ker}f \to N$が誘導される.
NST-28-2から, $\widetilde{f}$による同型$M/\mathrm{Ker}f \cong \mathrm{Im}f$が成り立つ.
(2)は(1)に従う.
$\square$
$2$つの加群を比較するときの物差しが、$1$つの線形写像で説明できることがわかりました。
線形写像を定義した際に、核と単射性の同値性を示しましたが準同型定理からも納得できます。
- $F:M \to N$を$R$線形写像とすると, $M/\mathrm{Ker}f \cong \mathrm{Im}f$.
- $f$が単射$\iff \mathrm{Ker}f=(0) \iff M/\mathrm{Ker}f =M/(0) \cong M$($1_{M}$で準同型定理).
準同型定理の系たち
準同型定理のすごさは、結果がいつでも成り立つことによる同型の構成です。
以下は準同型定理の系になります。(書籍によっては第$2,3$同型定理と呼ばれるもの)
$M$を$R$加群とし, $N,P$をその部分加群とする.
(1)$N/(N \cap P) \cong (N+P)/P$,
(2)$P \subset N \Rightarrow (M/P)/(N/P) \cong M/N$.
$i:N \to N+P$を包含写像, $\pi:N+P \to (N+P)/P$を自然な準同型とする.
このとき,$\pi i:N \to (N+P)/P$が得られる.
準同型定理から, $\pi i$の全射性と$\mathrm{Ker}(\pi i)=N \cap P$を示せば十分である.
任意の$\overline{n+p} \in (N+P)/P(n \in N,p \in P)$に対し,
$\overline{n+p}=\overline{n}$から$(\pi i)(n)=\overline{n}$となり全射である.
$\mathrm{Ker}(\pi i)=N \cap P$について, $n \in N$に対する以下の同値性から成り立つ.
$$\begin{align*}n \in \mathrm{Ker}(\pi i) &\iff (\pi i)(n)=\overline{n}=\overline{0}\\ &\iff n \in P\\ &\iff n \in N \cap P. \end{align*}$$
$\square$
自然な準同型$\pi:M \to M/P,\phi:M/P \to (M/P)/(N/P)$を取る.
準同型定理から, $\Phi=\phi \pi$の全射性と$\mathrm{Ker}\Phi=N$を示せば十分である.
全射性は, 全射である自然な準同型の合成より成り立つ.
$\mathrm{Ker}\Phi=N$について,
任意の$n \in \mathrm{Ker}\Phi$を取ると, $\Phi(n)=\overline{(\overline{n})}=\overline{\overline{0}}$となる.
従って, $\overline{n}=\overline{n}-\overline{0} \in N/P$からある$p \in P$により$n+p \in N$.
$P \subset N$から, $n \in N$となる.
逆に$n \in N$を取ると, $\overline{n} \in N/P$より$\overline{(\overline{n})}=\overline{\overline{0}}$である.
従って, $n \in \mathrm{Ker}\Phi$となる.
$\square$
気づいていると思いますが、(2)については剰余での部分加群の対応をしっかり使っています。
(部分加群ではないと定義できませんから…)
また(1)は(2)の仮定を付けると何も意味しない同型になります。
- $P \subset N$を仮定すると$N \cap P=P,N+P=N$,
- $N/P =N/(N \cap P) \cong (N+P)/P=N/P$.(同型部分が(1)の主張)
少し簡単な例で確認してみます。
$M=\{a+bX+cX|a,b,c \in \mathbb{Z}\}$:整数係数の$2$次以下の多項式全体の集合
$M$は$1,X,X^{2}$により生成される$\mathbb{Z}$加群(有限生成)
MOD1-6-3(1)の例
- $N=\mathbb{Z}+\mathbb{Z}X,P=\mathbb{Z}X+\mathbb{Z}X^{2}$はそれぞれ$M$の部分加群,
- $N \cap P=\mathbb{Z}X, N+P=\mathbb{Z}+\mathbb{Z}X+\mathbb{Z}X^{2}=M$より,
- $N/(N \cap P)=(\mathbb{Z}+\mathbb{Z}X)/\mathbb{Z}X \cong \mathbb{Z}$,
- ($f:\mathbb{Z}+\mathbb{Z}X \to \mathbb{Z}(a+bX \mapsto a)$で準同型定理)
- $(N+P)/P=M/(\mathbb{Z}X+\mathbb{Z}X^{2}) \cong \mathbb{Z}$,
- ($g:M/(\mathbb{Z}X+\mathbb{Z}X^{2}) \to \mathbb{Z}(a+bX+cX^{2} \mapsto a)$で準同型定理)
- $N/(N \cap P)=(\mathbb{Z}+\mathbb{Z}X)/\mathbb{Z}X \cong \mathbb{Z}$,
- 確かに, $N/(N \cap P) \cong \mathbb{Z} \cong (N+P)/P$になっている.
MOD1-6-3(2)の例
- $N=\mathbb{Z}X+\mathbb{Z}X^{2},P=\mathbb{Z}X$はそれぞれ$M$の部分加群かつ$P \subset N$,
- $M/N \cong \mathbb{Z}$
- $f:M \to \mathbb{Z}(a+bX+c \mapsto a)$で準同型定理
- $M/P \cong \mathbb{Z}+\mathbb{Z}X^{2}$
- $g:M \to \mathbb{Z}+\mathbb{Z}X(a+bX+cX^{2} \mapsto a+bX)$で準同型定理
- $N/P \cong \mathbb{Z}X^{2}$
- $h:N \to \mathbb{Z}X^{2}(bX+cX^{2} \mapsto cX^{2})$で準同型定理
- $M/N \cong \mathbb{Z}$
- $(M/P)/(N/P) \cong \mathbb{Z} \cong M/N$
- 1-6-5(2)と同じように写像を構成する.
MOD-1-6-5(2)は、$2$回剰余を取るため上下の剰余加群が同型でもそれを書き換えられるかは難しいところです。(今回は直感的にできそう感はありますが…)
具体的な例でも準同型定理を利用していますが、MOD1-6-3からすべて飛ばして同型とできます。
また例での準同型定理の使い方から、「同型を示せ」といった問題や「$\cong$が成り立つ」の確認では、線形写像を作るなら次の視点が役立ちます。
- 剰余加群から一般の加群へ写像を考える,
- $2$の加群がともに剰余加群ならば, 割っている加群(分母側)で単純な方が核になるよう写像を考える.
- 1.と2.のどちらも見えない場合は頑張って作る(大抵は無理なので別の方針を立てます)
おわりに
集合論を認めてしまうと、準同型定理はほぼ当たり前の事実だといえます。
線形写像だと、核が誘導写像が単射になる条件を満たしてくれることが鍵だとみれば理解しやすいと思います。
以上、ケンけんでした。