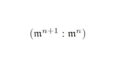こんにちは!ケンけんです。
今回は、剰余体と局所化を通した同型を見ていきます。
それでは行ってみよう!
キーワード:剰余体・局所化
この記事では、環はすべて単位的可換環とします。
今回の課題
今回の課題は次の主張です。
$R$を環とし, $\mathfrak{m} \in \mathrm{Max}R$を取る.
$A=R_{\mathfrak{m}}$を局所化, $N=\mathfrak{m} R_{\mathfrak{m}}$とする.
($(A,N)$は局所環.)
このとき, $k=R/\mathfrak{m}$線形空間として次の同型が成り立つ.
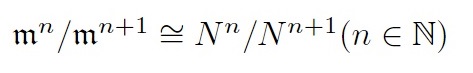
ちなみに動機となった命題は松村先生の「可換環論」の命題13.8です。
こちらは、$R$が体上の有限生成代数($k[\xi_{1}, \cdots, \xi_{r}]$で$\xi_{i}$は次数$1$の元)という制約つきです。
(つまり次数付き環)
でも、こんなの普通の環でも成り立つのでは?と思い調べたわけです。
剰余体 その他使う事実
まず、準備として認める主張を挙げていきます。
$R$を環とし, $S \subset R$を積閉集合, $I \subset R$をイデアルとする.
$\overline{S}$を$S$の$R/I$上の像とする.
(自然な準同型による像集合)
このとき, 次の同型が成り立つ.
$$R_{S}/IR_{S} \cong (R/I)_{\overline{S}}$$
$R$を環とし, $\mathfrak{m} \in \mathrm{Max}R$を取る.
各$n \in \mathbb{N}$で$\mathfrak{m}^n \neq \mathfrak{m}^{n+1}$ならば$\mathfrak{m}=(\mathfrak{m}^{n+1}:\mathfrak{m}^n)$である.
特に, 各$n \in \mathbb{N}$で$\mathfrak{m}^n/\mathfrak{m}^{n+1}$は$R/\mathfrak{m}$線形空間である.
体$k$の局所化は同型を通して$k$自身である.
$R, T$を環とし, $I \subset R$をイデアルとする.
環準同型写像$f:R \rightarrow T$における拡大イデアルを$IT$とあらわす.
このとき, 各$n \in \mathbb{N}$に対し$(IT)^n =I^nT$である.
証明
それでは示していきます。
結構長めなので要点事に分割します。
命題1より,
$A/N=R_{\mathfrak{m}}/\mathfrak{m}R_{\mathfrak{m}} \cong (R/\mathfrak{m})_{\overline{R \backslash \mathfrak{m}}}$.
命題3から, $R/\mathfrak{m}=k$より$k \cong k_{\overline{R \backslash \mathfrak{m}}}$.
$R/\mathfrak{m} \cong A/N$である.
$n \in \mathbb{N}$を任意とする.
命題2より次が成り立つ.
$\mathfrak{m}^n/\mathfrak{m}^{n+1}$は$k$線形空間,
$N^n/N^{n+1}$は$A/N$線形空間.
$R/\mathfrak{m} \cong A/N$より, $N^n/N^{n+1}$は$k$代数として$k$線形空間とみなせる.
$g:\mathfrak{m}^n/\mathfrak{m}^{n+1} \rightarrow N^n/N^{n+1}$
($x+\mathfrak{m}^{n+1} \mapsto x/1+N^{n+1}$)
を定義する.
well-definedについて(ほとんど明らかなので省略可)
$x+\mathfrak{m}^{n+1}=y+\mathfrak{m}^{n+1} \in \mathfrak{m}^n/\mathfrak{m}^{n+1}$を仮定する.
$g(\mathfrak{m}^{n+1}) \subset N^{n+1}$より次が成り立つ.
$x-y \in \mathfrak{m}^{n+1}$から$(x-y)/1 \in N^{n+1}$.
従って, $x/1+N^{n+1}=y/1+N^{n+1}$である.
$k$線形性は、加群の自然な写像と同様である.
(加群$M, f:M \rightarrow M_{\mathfrak{m}}(m \mapsto m/1)$)
以後, 次のように記述する.
$x+\mathfrak{m}^{n+1}=\overline{x} \in \mathfrak{m}^n/\mathfrak{m}^{n+1}$,
$x/s+N^{n+1}=\overline{x/s} \in N^n/N^{n+1}$
全射について
任意の$\overline{x/s} \in N^n/N^{n+1}$を取る.
このとき, $x \in \mathfrak{m}^n,s \notin \mathfrak{m}$である.
従って, $(s+\mathfrak{m})^{-1}\leftrightarrow (s/1+N)^{-1}$.
また, $\overline{x/s}=(s/1+N)^{-1}(\overline{x/1})$である.
これより, 次の変形ができる.
$\overline{x/s}=g((s+\mathfrak{m})^{-1}\overline{x})$.
$(s+\mathfrak{m})^{-1}\overline{x} \in \mathfrak{m}^n/\mathfrak{m}^{n+1}$より, $g$は全射である.
単射について$\mathrm{Ker}g=\{\overline{0}\}$を示せば十分.
$\overline{x} \in \mathrm{Ker}g$をとると, $\overline{x/1}=\overline{0/1}$となる.
命題4から$N^{n+1}=\mathfrak{m}^{n+1}R_{\mathfrak{m}}$.
よって, ある$m/t \in N^{n+1}(m \in \mathfrak{m}^{n+1},t \notin \mathfrak{m})$で,
$x/1=m/t$が成り立つ.
ある$v \notin \mathfrak{m}$で次のようになる.
$vtx=vm \in \mathfrak{m}^{n+1}$.
従って, $\overline{vtx}=\overline{0}$となる.
$vt \notin \mathfrak{m}$より, $0 \neq vt+\mathfrak{m} \in k$である.
これより, 次が成り立つ.
$\overline{x}=(vt+\mathfrak{m})^{-1}\overline{vtx}=\overline{0}$.
よって, $\mathrm{Ker}g=\{\overline{0}\}$である.
$\square$
さて、今回の同型も局所化と剰余なのでこの記事のように示せるのではと思えます。
しかし、テンソル積の同型変形は同じ加群同士である必要があります。
実際に、$R$と$A=R_{\mathfrak{m}}$の差が悪さをしています。
なので、$M^{n}/M^{n+1}$を変形して$\mathfrak{m}^n/\mathfrak{m}^{n+1}$にすることができません。
考える環は、$R$ではなく剰余体$k=R/\mathfrak{m}$であるのも同型変形の足かせになります。
別証明(2024/5/7 追加)
課題の同型は、次の主張で写像を構成せずに証明できました。(ぴえん)
$R$を環とし, $S \subset R$を積閉集合とする.
$M$を$R$加群とし, $I \subset R$をイデアルとする.
$\overline{S}$を$S$の$R/I$上の像とする.
このとき, $R/I$加群として次の同型が成り立つ.
$$M_{S}/IM_{S} \cong (M/IM)_{\overline{S}}$$
拡大イデアルとして次が成り立つ.
$N^n=\mathfrak{m}^nR_{\mathfrak{m}}=(\mathfrak{m}^n)_{\mathfrak{m}}$.
命題5より次の同型が得られる.
$(\mathfrak{m}^n)_{\mathfrak{m}}/\mathfrak{m}(\mathfrak{m}^{n})_{\mathfrak{m}} \cong (\mathfrak{m}^n/\mathfrak{m}^{n+1})_{\overline{\mathfrak{m}}}$.
$N^{n}/N^{n+1} \cong (\mathfrak{m}^n/\mathfrak{m}^{n+1})_{\overline{\mathfrak{m}}}$.
$R/\mathfrak{m}$は体より, $R/\mathfrak{m}$線形写像として次の同型が得られます.
$(\mathfrak{m}^n/\mathfrak{m}^{n+1})_{\overline{\mathfrak{m}}} \cong \mathfrak{m}^n/\mathfrak{m}^{n+1}$
悔しいでス!!とても単純ですわ。
おわりに
今回の主張は、証明の本題部分ではありませんがさも当たり前のようになっていたため示しました。
結構これを示すためにいろいろ別で示したので、それもまた別で書こうと思います。
以上、ケンけんでした。
命題2についてはこちら
命題5については(整備中)
参考文献
[1]松村英之, 復刊 可換環論, 共立出版