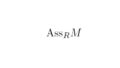こんにちは!ケンけんです。
今回は、松村先生の「可換環論」を読んでいて??となった「~はArtin環となる」を解決しようとしたらいろいろわかったので記事を書いていきます。
それではいってみよう!
キーワード:半局所環・定義イデアル
この記事では、環はすべて単位的可換環とします。
確認 ネーター半局所環
まずは、半局所環の定義を復習しておきます。
$R$:環
$\mathrm{Max}R$:$R$の極大イデアル全体の集合
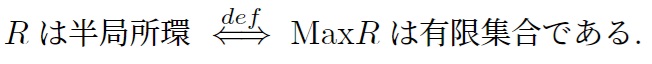
局所環はただ一つの極大イデアルを持つ環で、半局所環は有限個に緩めたものとなります。
単純な例だと次のものがあります。
- $R=k[X],I=/(X^2-3X+2)$について$\mathrm{Max}R/I=\{(X-1)/I,(X-2)/I\}$
- Artin環は半局所環である.
このように多項式環で局所環より多く作ることもできます。
また、本題の前に使用する事実と使用する定義を挙げておきます。
$R$を環とする.
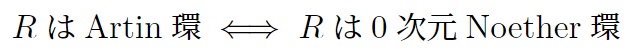
$R$を環とし, $I_{1}, \ldots , I_{n} \subset R$をイデアル, $\mathfrak{p} \in \mathrm{Spec}R$とする.
$\bigcap_{i=1}^{n}I_{i} \subset \mathfrak{p} \Rightarrow \exists j \; s.t. \; I_{j} \subset \mathfrak{p}$
どちらも環論では重要な結果です。
$A$:Noether半局所環
$M=J(R)$:$A$のJacobson根基
$I \subset R$:イデアル
$I \subset$:定義イデアル $\overset{def}{\iff} \exists m >0 \; s.t. \; M^m \subset I \subset M$.
この定義、動機となった本以外では使っておらず、ネットで検索しても出てきません。
なのでこの本特有と言いたいのですが、ちょっとした特徴づけもできました。
本題からずれるため、次の記事で単独で取り上げます。
今回はこれらを利用して問題を考えていきます。
動機と課題
それでは動機となった部分を見ていきます。
次の部分は、$A$をNoether半局所環, $I$を定義イデアルを前提とします。
$A_{0}’=A/I$はアルティン環であり, $I=\overset{r}{\underset{1}{\sum}} x_{i}A$ならば$x_{i}$を$I/I^2$における像を$\xi_{i}$とすれば$A’=A_{0}'[\xi_{1}, \ldots , \xi_{r}]$である.
松村英之, 復刊 可換環論, 共立出版, p118
今回引っかかったのは、$A/I$がArtin環となることです。
この数ページ後に加群の長さを考えるのでアルチン環である必要があります。
しかし、なぜそうなのかの説明がされていないためいろいろ調べることになりました。
ということで今回の課題は次のようになります。
$R$をNoether半局所環, $I \subset R$を定義イデアルとする.
- $R/I$はArtin環である.
$R$がNoether環より剰余環$R/I$もNoether環となる.
定理1から, $\mathrm{dim}R/I=0$を示せば十分である.
素イデアルの対応原理から, $\mathcal{V}(I) \subset \mathrm{Max}R$であることを示せば十分である.
$R$は半局所環より, $\mathrm{Max}R=\{\mathfrak{m}_{1}, \ldots , \mathfrak{m}_{n}\}(n \geq 1)$となる.
Jacobson根基を$M=\bigcap_{i=1}^{n}\mathfrak{m}_{i}$とおく.
$I$は定義イデアルなので, ある$m >0$で$M^m \subset I \subset M$が成り立つ.
任意の$m>0$で$\sqrt{M^m}=M$より, 各辺で根基を取ると$M \subset \sqrt{I} \subset M$となる.
従って, $\sqrt{I}=M$となる.
次に, $\mathfrak{p} \in \mathcal{V}(I)$を取ると, $I \subset \mathfrak{p}$である.
この両辺に根基を取ると次のようになる.
$M=\sqrt{I} \subset \sqrt{\mathfrak{p}}=\mathfrak{p}$.
ここで, 定理2からある$i$で$\mathfrak{m}_{i} \subset \mathfrak{p}$となる.
$\mathfrak{i}$の極大性から, $\mathfrak{m}_{i}=\mathfrak{p} \in \mathrm{Max}R$.
以上から, $\mathrm{Spec}R/I =\mathrm{Max}R/I$より$\mathrm{dim}R/I=0$である.
$\square$
この証明では次がポイントになっています。
- 半局所環であること
- 素イデアルの対応
1.半局所環であること
実は定理2(prime avoidance)は、有限個のイデアルの共通部分であることが必要です。
無限個版を考えている論文等でも一般の場合ではなくいくつか条件を付けています。
そのため、極大イデアルが有限個であることに意味があります。
2.素イデアルの対応
以前の記事で取り上げたイデアル対応原理ですが、こんなところでも使えます。
そして剰余環上だと、$\mathrm{Max}R/I \subset \mathrm{Spec}R/I$がいえて次元$0$であることがすぐにわかります。
($R$上では$\mathcal{V}(I)$以外の極大イデアルがあり得るので「$\subset$」までしかわかりません。)
おわりに
トピックが別となる定義イデアルについては次の記事に続きます。(こちら)
ほとんど触らない半局所環とJacobson根基の性質の学習としてちょうどよかったと思います。
(これも平文でしれっと流しているのだから数学書は恐ろしい。)
以上、ケンけんでした。
参考文献
松村英之, 復刊 可換環論, 共立出版