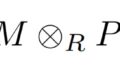こんにちは!ケンけんです。
以前加群$M$のねじれ元だけからなるtorsion submodule$T(M)$を取り上げました。
今回は、その別表現を通じて次の2つを使い調べたことを書いていきます。
- $2$のべき乗による剰余環(加群)
- Krull’s intersection Theorem(クルルの交叉定理)
それでは行ってみよう!
キーワード:torsion submodule
$\mathbb{Z}/2\mathbb{Z}$の基本事実
まずは、環としての基本性質から見ていきます。
- $\mathbb{Z}/2\mathbb{Z}$は体である.($2\mathbb{Z}$が極大イデアルより)
- $\mathbb{Z}/2^n\mathbb{Z}(n \geq 2)$は整域ではない.($2^n\mathbb{Z}$が素イデアルではないため)
- $\mathbb{Z}/2^n\mathbb{Z}(n \geq 1)$は単元と零因子しか持たない.
- $\mathbb{Z}/2^n\mathbb{Z}(n \geq 1)$は$(\overline{2})$を極大イデアルとする$0$次元局所環である. (理由 参考)
- 有限環よりArtin環かつNoether環である.
次に加群としての性質を見ていきます。
- $\mathbb{Z}/2^n\mathbb{Z}(n \geq 2)$は$\mathbb{Z}$上はtorsion moduleである. (正則元$2^n$で零化される.)
- $\mathbb{Z}/2^n\mathbb{Z}(n \geq 2)$は$\mathbb{Z}/2^m\mathbb{Z}(m \geq n)$上はtorsion-free moduleである.
- ($\mathrm{Ann}_{\mathbb{Z}}\mathbb{Z}/2^n\mathbb{Z}=(2^n)$より$I \subset \mathrm{Ann}_{\mathbb{Z}}\mathbb{Z}/2^n\mathbb{Z}$で$\mathbb{Z}/I$加群となる.)
torsion module $\mathrm{Ker}$による表示
以前取り上げたtorsion submodule$T(M)$は次のように別の表現を持ちます。
$R$を環とし, $M$を$R$加群, $S=\mathrm{Reg}R$とする.
このとき, 自然な写像$f:M \rightarrow M_{S}(m \mapsto m/1)$について$T(M)=\mathrm{Ker}f$である.
$m \in T(M)$について, ある$r \in \mathrm{Reg}R$で$rm=0$である.
従って$M_{S}$上で, $m/1=rm/r=0$であるため$m \in \mathrm{Ker}f$である.
逆に$m \in \mathrm{Ker}f$について, $m/1=0$である.
従って, ある$r \in \mathrm{Reg}R$で$rm=0$より$m \in T(M)$である.
$\square$
$M_{S} \cong M \otimes_{R}R_{S}$より、$T(M)=\mathrm{Ker}(M \rightarrow M \otimes_{R}R_{S})$と書いている本もありますね。
なぜKrull’s intersection Theoremが?
Krull’s intersection Theoremの主張は、次の加群版が一般的な形になります。
$R$をNoether環とし, $M$を有限生成$R$加群, $I$をそのイデアルとする.
- $\bigcap_{i=1}^{\infty}I^iM=\{m \in M|\exists a \in 1+I \; s.t. \; ax=0\}$
この共通部分は、加群の完備化$\widehat{M}$について次の自然な写像の核になります。
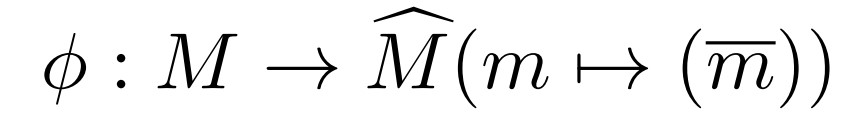
(逆極限による完備化についてはこちら)
この核は、位相がハウスドルフかの判定になるなど重要ですが今回の興味は別にあります。
それは、$S=1+I$の元で零化されることです。
これは積閉集合になっており、環も加群も局所化を考えられます。
そして、次の局所化の自然な写像と核が一致します。
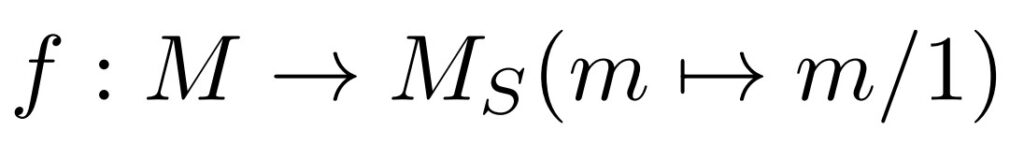
$x \in \mathrm{Ker}\phi$を取ると, 各$i$で$x \in I^{i}M$である.
従って, $x \in \bigcap_{i=1}^{\infty}I^{i}M$である.
$M$は有限生成よりKrull’s intersection Theoremから, ある$a \in 1+I$で$ax=0$である.
したがって, $f(x)=x/1=ax/a=0$となり$x \in \mathrm{Ker}f$である.
逆に, $x \in \mathrm{Ker}f$を取ると, ある$a \in S$で$ax=0$を満たす.
再びKrull’s intersection Theoremから, $x \in \bigcap_{i=1}^{\infty}I^{i}M$を満たす.
以上から, 各$i$で$x \in I^{i}M$より$\phi(x)=(\overline{x})=(\overline{0})$である.
よって, $x \in \mathrm{Ker}\phi$である.
$\square$
この時、次の疑問が出てきます。
$1+I=\mathrm{Reg}R$となるようなイデアル$I \subset R$は具体的にどんなものがあるか?
これが見つかれば、$T(M)$がイデアル倍の部分加群で表現できることになります。
そして、例として見つけたのが今回の題材「$R=\mathbb{Z}/2^n\mathbb{Z}$」です。
$\overline{1}+(\overline{2})=\mathrm{Reg}(\mathbb{Z}/2^n\mathbb{Z})$になります。
わかったことと課題
さて$\mathbb{Z}/2^n\mathbb{Z}$上の有限生成加群には、適用でき$I^n=(\overline{2})^n=0$です。
従って、どのような有限生成加群$M$についても$T(M)=\bigcap_{i=1}^{n}I^iM= 0$となります。
以上から、$\mathbb{Z}/2^n\mathbb{Z}$上の有限生成加群は必ずtorsion-freeになることがわかりました。
ここまでは、調べられたのですが他の$1+I=\mathrm{Reg}R$の例が見つけられていません。
また今回は有限生成加群はtorsion-freeになりましたが、ほかの例ではどうなるかわかりません。
なので次の2つが残った課題になります。
- $\mathbb{Z}/2^n\mathbb{Z}$以外の$1+I=\mathrm{Reg}R$の例は存在するか?
- 他の例が存在する場合、その環上の有限生成加群はtorsion-freeなどが決まるか?
おわりに
今回の記事は結構書き始めたのは早かったですが、いざ書き始めるとほかの例が見つからず出すのが遅れました。こういう調べもの記事は80%ぐらいの状態で出すほうがいいのかもしれない。
反例を作ればいいタイプじゃない問題は、探すのが大変ですが気が向いたらまた探すとします。
以上、ケンけんでした。