こんにちは!ケンけんです。絶対に理解するHom関手第3弾です。
今回は、圏と関手をものすごく単純に定義して$\mathrm{Hom}$を取る操作を圏論的に見ます。
それでは行ってみよう!
キーワード:加群の圏
この記事では、環はすべて単位的可換環とします。
圏と関手
圏と関手について復習しますが、厳密に考えようとすると沼で永遠に話が先に進みません。
そこで今回は、ある種ユークリッド幾何の線や点のように「こういう名前で公理化するよ」と言う体で考えます。
(圏論の本ですらあまりここに言及しないので定義の行間を埋めるのはとても大変)
(注:以下の定義は議論の簡便化のため一般の圏ではなく局所小($\rm{locally \; small}$)な圏です。)
$(1)$ クラス($\rm{class}$)とはモノの集まりである.
圏$\mathcal{C}(\rm{category})$は次の2つのクラスからなる.
$(1)$ $\mathrm{Ob}(\mathcal{C})$:対象($\rm{object}$)のクラス
$X \in \mathrm{Ob}(\mathcal{C})$は, $X$が対象であることを意味する.($X \in \mathcal{C}$と略する.)
$(2)$ $\mathrm{Hom}_{\mathcal{C}}(X,Y)$:対象$X$から$Y$への射($\rm{morphism}$)の集合
($\mathrm{Mor}(\mathcal{C})$で$\mathcal{C}$のすべての射のクラスを表す.)
$(3)$ $X,Y,Z \in \mathcal{C}$に対して, 次を射の結合と呼ぶ.
- $\circ:\mathrm{Hom}_{\mathcal{C}}(X,Y) \times \mathrm{Hom}_{\mathcal{C}}(Y,Z) \rightarrow \mathrm{Hom}_{\mathcal{C}}(X,Z)((f,g) \mapsto g \circ f)$
- $\circ$は結合律を満たす.
$(4)$ 各$X \in \mathcal{C}$に対し次の恒等射$\mathrm{id}_{X} \in \mathrm{Hom}_{\mathcal{C}}(X,X)$が存在する.
$ \;$$\forall f \in \mathrm{Hom}_{\mathcal{C}}(X,Y), \forall g \in \mathrm{Hom}_{\mathcal{C}}(W,X)(f \circ \mathrm{id}_{X}=f, \mathrm{id}_{X} \circ g=g)$.
「すべての集合の集まりは集合にならない」ことは有名で、クラスとは集合ではありません。
(集合の定義は「明確に範囲が定まる、明確な対象」集まりで設定がついている。参考)
集合はクラスの一種であり、「すべての集合の集まり」は集合ではなくクラスになります。
そのため、射の合成はいかにも写像の合成のようですが違うものと思いましょう。
(クラスの直積も定義していないため、そのままでは普通考えられない。)
厳密に議論すると、数学基礎論になるので「こういう」入れ物を定義したと思ってください。
ちなみに、命題論理や述語論理は集合だけに定義されたものではないため記号($\Rightarrow$など)は利用しても問題ありません。
これを前提に、本題$\mathrm{Hom}$関手に関係する関手を定義します。
$\mathcal{C}, \mathcal{C}’$:圏
$F:\mathcal{C} \rightarrow \mathcal{C}’$が関手($\rm{functor}$)であるとは次を満たすことである.
$(1)$ $X \in \mathcal{C} \Rightarrow F(X) \in \mathcal{C}’$
$(2)$ $\forall X,Y \in \mathcal{C}(f \in \mathrm{Hom}_{\mathcal{C}}(X,Y) \Rightarrow F(f) \in \mathrm{Hom}_{\mathcal{C}’}(F(X),F(Y)))$
$(3)$ $\forall X \in X(F(\mathrm{id}_{X})=\mathrm{id}_{F(X)})$
$(4)$ $f \in \mathrm{Hom}_{\mathcal{C}}(X,Y),g \in \mathrm{Hom}_{\mathcal{C}}(Y,Z) \Rightarrow F(g \circ f)=F(g) \circ F(f)$
$\mathcal{C}, \mathcal{C}’, \mathcal{C}^{”}$を圏とし, 関手$F:\mathcal{C} \rightarrow \mathcal{C}’, G:\mathcal{C}’ \rightarrow \mathcal{C}^{”}$の合成$G \circ F$を次のように定義する.
- $X \in \mathcal{C} \Rightarrow (G \circ F)(X)=G(F(X))$
- $f \in \mathrm{Mor}(\mathcal{C}) \Rightarrow (G \circ F)(f)=G(F(f))$
関手は, 共変関手($\rm{covariant \; functor}$)とも呼ぶ.
$F$は反変関手($\rm{contravariant \; functor}$) であることを次で定義する.
- 関手と同様に(1),(3)を満たす.
- $\forall X,Y \in \mathcal{C}(f \in \mathrm{Hom}_{\mathcal{C}}(X,Y) \Rightarrow F(f) \in \mathrm{Hom}_{\mathcal{C}’}(F(Y),F(X)))$
- $f \in \mathrm{Hom}_{\mathcal{C}}(X,Y),g \in \mathrm{Hom}_{\mathcal{C}}(Y,Z) \Rightarrow F(g \circ f)=F(f) \circ F(g)$
反変関手は、射の方向を逆方向にすると思えば十分です。
ちなみに反変関手は反対圏$\mathcal{C}^{op}$(射が逆方向の圏$\mathcal{C}$)を使うと、共変関手と見ることもできます。
対象全体と射全体が集合なら、関手は2つの写像を同時に考えていることになります。
射が満たす合成や結合律もすべて集合の世界まで制限すると「対象=集合」、「射=写像」です。
ここから、圏は集合と写像のセットをより広く考えているのだとわかります。
Hom関手 実際どうなのか?
厳密さを一度おいて、上の定義をすべて加群と$\mathrm{Hom}$関手に置き換えてみます。
$\mathcal{C}=\mathrm{Mod}R$:$R$加群の圏(左$R$加群の圏)
対象:$R$加群($M,N$など)
射:$R$線形写像全体($M,N \in \mathrm{Mod}R$について$\mathrm{Hom}_{R}(M,N)$)
$N \in \mathrm{Mod}R$について
- $\mathrm{Hom}_{R}(-,N):\mathrm{Mod}R \rightarrow \mathrm{Mod}R(M \mapsto \mathrm{Hom}_{R}(M,N)) $(反変関手)
- $\mathrm{Hom}_{R}(N,-):\mathrm{Mod}R \rightarrow \mathrm{Mod}R(M \mapsto \mathrm{Hom}_{R}(N,M)) $(共変関手)
この表現に従うとこれまで調べたことは次に対応していました。
(1)や(3)はほとんど明らかでした。((1)の確認は記事1の初めの命題)
そして、記事2で考えた完全列と$\mathrm{hom}_{R}(-,P), \mathrm{hom}_{R}(P,-)$を取った列の対応を図で書くと次のようになります。
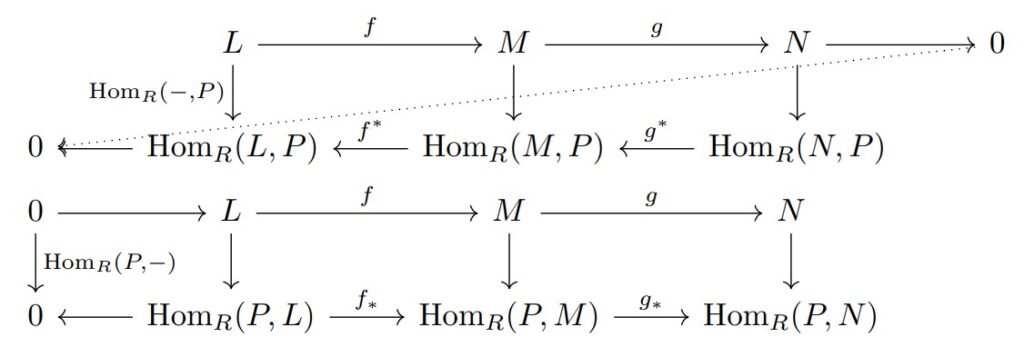
図:完全列と$\mathrm{Hom}$関手の対応
横方向(完全性)を考えていましたが、縦方向に$\mathrm{Hom}$関手を取る操作があったわけです。
関手が写像ではない(加群の圏が集合ではないため)ので、加群の可換図式とは言えません。
なので、縦方向の矢印は加群が関手を通して対応しているだけと思ってください。
(あまり、射と関手を一緒に書くことはない。)
定義域と値域を同時に動かすと?
関手としての特徴づけが終わったところで、再び純粋な$\mathrm{Hom}$関手の性質を見ます。
ここまでは()内の加群を一方固定していましたが、同時に2つ動かすとどうなるでしょう。
例えば次のような状況を考えます。
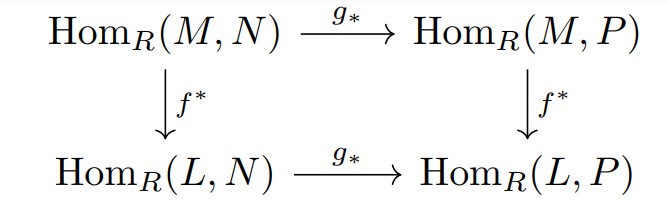
図:$f:L \rightarrow M,g:N \rightarrow P$について
加群をずらす場合は、$*$付き写像を取ればよかったです。
上の図では同じ$f^{*},g_{*}$を使っていますが、それぞれ定義域と値域は変わっています。
上の図式は、可換図式になっており上付きと下付き写像の可換性がわかります。
$L,M,N,P$を$R$加群とし, $f \in \mathrm{Hom}_{R}(L,M), g \in \mathrm{Hom}_{R}(N,P)$とする.
このとき, $f^{*} \circ g_{*}=g_{*} \circ f^{*}$である.
つまり次の図式は可換である.
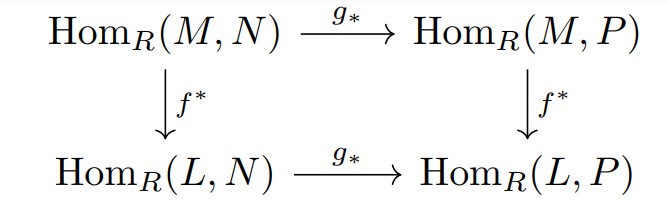
任意の$h \in \mathrm{Hom}_{R}(M,N)$を取る.
このとき, $(f^{*} \circ g_{*})(h)=f^{*}(g \circ h)=g \circ h \circ f=g_{*}(h \circ f)=(g_{*} \circ f^{*})(h)$である.
$\square$
同じ表記を利用していますが、$*$付きが交換できることだけで十分ですね。
この場合は、$\mathrm{Hom}_{R}(-,-)$で$\rm{bifunctor}$と呼ばれるものになります。
おわりに
今回はほとんど圏と関手の話題で占めてしまいあまり面白味の無いものになってしまいました。
これまで積み上げた$\mathrm{Hom}$を取る操作の整理になりました。
あとは、雑多な性質をまとめると一旦シリーズは完結です。
以上、ケンけんでした。