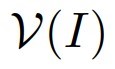こんにちは!ケンけんです。前回は決まった倍数全体の集合が、イデアルと言うベクトルのような演算を持つ部分集合が見つかりました。
今回は、そのイデアルの骨組みがわかる「生成されたイデアル」を取り扱います。
キーワード:生成されたイデアル・生成系
この記事では、環はすべて単位的可換環とします。
導入
「生成」とは、辞書などで次のように書かれています。
せいせい 【生成】ーする(自他サ)
物としての形が表れる(を現す)こと
新明解 国語辞典, 2013, 三省堂, p813
これを頭に置いて、単純なケースから見ていきましょう。
1.イデアルとしての環全体
イデアルの定義から、環$R$全体もイデアルだと言うことはすぐにわかります。
そして、すべての$r \in R$について$r \times 1_{R}=r \in R$です。(単位元の性質を利用)
少し回りくどく環$R$を書こうとすると、次のようになりますね。
$$R=\{r \in R|r=r \times 1_{R}\}$$
単位元を通して$R$が表れるので、$R$は単位元から「生成された」イデアルだと言えます。
ちなみに、単位元とイデアルは次のような性質を持ちます。
$R$を環とし, $I \subset R$をイデアルとする.
このとき, 次が成り立つ.
$R=I \iff 1_{R} \in I$
$\Rightarrow$については$1_{R} \in R=I$から明らかである.
$\Leftarrow$について
$1_{R} \in I$から, 任意の$r \in R$について$r=r \times 1_{R} \in R$である.
従って, $R \subset I$より$R=I$である.
$\square$
2.整数環の倍数 イデアル
整数の倍数全体の集合がイデアルであることは前回見ました。
例えば、$2$の倍数によるイデアル$I=\{x \in \mathbb{Z}|\exists k \in \mathbb{Z} \;s.t. \; x=2k\}$を取り上げます。
$I$の元は、必ず$2$に適当な整数をかけた数と書けることに注目します。
$I$のことは、$2\mathbb{Z}$と書きましたこれは次のように書けます。
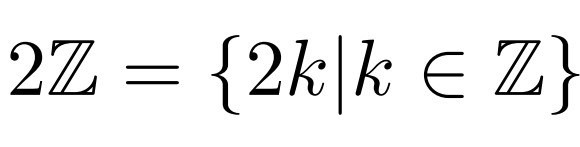
$a \in \mathbb{Z}$について「$a\mathbb{Z}=\{ak|k \in \mathbb{Z}\}$」とする集合は、$a$の倍数全体のイデアルです。
$2\mathbb{Z}$は、$2$を通して作られるイデアルです。
そのため、$I$は「$2$で生成されている」と言えます。
それでは、$2$の倍数と$3$の倍数の和で表せる集合はどうでしょう。
これは、イデアル「$2\mathbb{Z}+3\mathbb{Z}=\{2x+3y|x,y \in \mathbb{Z}\}$」となります。
ユークリッドの互除法を使うと「$2x+3y=1$」の解が存在するので$1 \in 2\mathbb{Z}+3\mathbb{Z}$です。
1-3-1より、$\mathbb{Z}=2\mathbb{Z}+3\mathbb{Z}$となってしまいます。
3.べき関数全体の集合
実変数の連続関数全体の集合$C(\mathbb{R})$は、単位的可換環だと第1回で取り上げました。
同様に実変数のべき関数全体$\mathbb{R}[x]=\{\sum_{i:有限個}r_{i}x^i|\forall i (r_{i} \in \mathbb{R})\}$も同様に環です。
(これは多項式環の一例です。)
1次以下の項を持たないべき関数全体$I=\{\sum_{i \geq 2}r_{i}x^i|\forall i (r_{i} \in \mathbb{R})\}$を考えてみます。
$I$は、$\mathbb{R}[x]$のイデアルになります。(示してみてください。)
適当な$f(x) \in I$は$f(x)=g(x) \times x^2(g(x) \in \mathbb{R}[x])$と書けます。
つまり、$I$は$x^2$で生成されていると言えます。
以上から、イデアルは特定の元を骨組みに作られる場合があります。
ここまでは1つの元で生成されるパターンでしたが、2つ以上の場合もあり得ます。
4.2つ以上の元で生成されるイデアル
$S=\{\cos x ,x\} \subset C(\mathbb{R})$を取ります。
「$\cos x ,x$で生成されている」を考えると、次のイデアルが考えられます。
$$I=\{f \cos x+g x|f,g \in C(\mathbb{R})\}$$
確かに、$\cos x, x$を骨組みにして作られた集合なので生成されたと言えそうです。
しかし、ここで$I$が$\cos x,x$で「生成されるイデアル」として妥当か問題になります。
また、「生成する」を言語としては納得しましたが定義はしていません。
数学用語である以上、何か基準を決めた定義にする必要があります。
生成の基準を決める
導入の「~で生成されたイデアル」は、「$~$($1_{R}$や$S$など)」を元に利用しています。
骨組みなので、少なくとも「$~$」の部分の元は含む必要があります。
「骨組み」と言うからには、生成する元たちは体で言う骨であってほしいです。
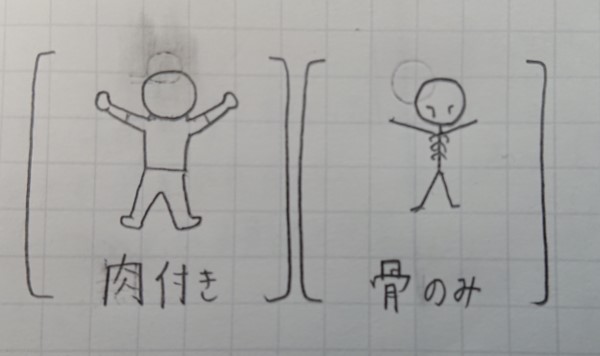
図:骨組みイメージ
生物は骨の上に筋肉やら皮膚やら臓器やらありますが、すべて骨を基本に上から覆っています。
ヒトの形で最も小さいものは、すべて骨だけの状態です。
従って、「骨組み」$=$「一番小さい人型」と言えます。
全順序集合かわからない場合は、最小の元(今回は部分集合)がわかりません。
しかし、集合の包含を使うと最小の部分集合を次のように書けます。
$X$を集合として, $S \subset X$を取る.
$T=\{Y \in 2^{X}|S \subset Y\}$を置く.
$(S)=\bigcap_{Y \in T}Y$を$S$で生成される部分集合と呼ぶことにする.
このとき, $(S)=S$であるため$S$を骨組みとする集合と言える.
これで$S \subset Y \in 2^{X}$について$(S) \subset Y$となり「$S$を含む部分集合」では最小になります。
$(S)$は、$S$を含む部分集合で包含関係で最も小さく取れています。
集合の場合は明らかですが、これに構造(加法など)を追加すると当然一致しません。
イデアルの場合は、部分集合$Y$がイデアルとすると$(S)$はイデアルです。
(イデアルの共通部分はイデアル)
イデアルだけでなく部分群・部分環・部分加群は同じように「生成された~」を定義します。
定義 生成されたイデアル
それでは定義していきます。
$R$:環 $S \subset R$ $X=\{U \in 2^{R}|S \subset U:$イデアル$\}$
$I \subset R$:イデアル
$(S)=\bigcap _{U \in X}U$:$S$により生成されるイデアル($\rm{an \; ideal \; generated \; by \; S}$)
$S$は$(S)$の生成系($\rm{generated \; system}$), その元を生成元($\rm{generator}$)と呼ぶ.
特に$S=\{s_{1}, \ldots , s_{m}\}$のとき, $(S)=(s_{1}, \ldots , s_{m})$と書く.
$I$は有限生成($\rm{finitely \; generated} $) $\overset{def}{\iff} \exists \{s_{1}, \ldots , s_{m}\} \subset R \; s.t. \; I=(s_{1}, \ldots , s_{m})$
$I=(x)(x \in R)$のとき, $I$は$x$で生成される単項イデアル($\rm{principal \; ideal}$)と呼ぶ.
生成されたイデアルは、有限個の場合はベクトルの一次結合のように書いていました。
実際に、次のように生成されたイデアルを具体的に表現できます。
$R$を環とし, $S \subset R$を取る.
このとき, 次が成り立つ.
$(1)$ $(S)=\{\sum_{i=1}^{m}r_{i}s_{i}|m \in \mathbb{N}, r_{i} \in R, s_{i} \in S, i=1, \ldots , m\}$
$(2)$ $S=\{s_{i} \in R|i=1, \ldots , m\} \Rightarrow (S)=(s_{1})+(s_{2})+ \cdots +(s_{m})$
$Y=\{\sum_{i=1}^{m}r_{i}s_{i}|m \in \mathbb{N}, r_{i} \in R, s_{i} \in S, i=1, \ldots , m\}$とおく.
各$s \in S$について$1_{R} s=s \in Y$より$S \subset Y$である.
$Y$がイデアルとなることは明らかである. (加法とスカラー倍の確認のみ)
従って, $(S)$の最小性から$(S) \subset Y$である.
逆は, 各イデアル$S \subset I \subset R$について$Y \subset I$を示せば十分である.
任意の$x=\sum_{i=1}^{m}r_{i}s_{i}(m \in \mathbb{N}, r_{i} \in R, s_{i} \in S)$について$s_{i} \in I$より$r_{i}s_{i} \in I$となる.
以上から, $x \in I$のため$Y \subset (S)$となる.
$\square$
$(1)$より$(S)=\{\sum_{i=1}^{m}r_{i}s_{i}|r_{i} \in R\}$と書ける.
従って, $Z=\{\sum_{i=1}^{m}r_{i}s_{i}|r_{i} \in R\}$とおき, $Z=(s_{1})+ \cdots +(s_{m})$を示せば十分である.
イデアルの和の定義から, $(s_{1})+ \cdots +(s_{m})=\{\sum_{i=1}^{m}a_{i}|a_{i} \in (s_{i})\}$である.
ここで各$x \in (s_{i})$は, $x=r_{i}s_{i}(r \in R)$と書けるため, $(s_{1})+ \cdots +(s_{m})=\{\sum_{i=1}^{m}r_{i}s_{i}|r_{i} \in R\}=Z$となる.
$\square$
導入の例はすべて有限生成なイデアルです。
- 環$R$自身は、$R=(1_{R})$,
- $a\mathbb{Z}=(a)(a \in \mathbb{Z})$,
- 2次以下の項を持たないべき関数全体$I$は、$I=(x^2)$,
- $\{\cos x,x\}$で生成されるイデアル$I$は、$I=(\cos x, x)$.
おわりに
「生成された~」は、イデアルだけでないことを既にあげました。
証明では、定義からわかる最小性を利用する場合があります。
なので、定義の方で理解した方が以後「生成された~」を見かけても同じだと導けると思ます。
以上、ケンけんでした。