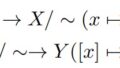こんにちは!ケンけんです。
前回は、集合をルールに従って部分集合で分ける「類別」を取り扱いました。
今回は、第2弾の主題「同値類」とそこから得られる「商集合」を取り扱います。
キーワード:同値類・商集合
導入
単射・全射の記事や前回の類別では、導入の中で動物の分類を取り上げました。
このとき、目・科・属と言った特定の集団にグループ分け指定ました。
そしてこのグループの分類の仕方に以前取り上げた同値関係が潜んでいます。
以前は猿がいるの目(霊長目)を使ったので今回はもっと単純に脊椎動物で考えます。

図:脊椎動物全体の分類と代表元だけで表した図
(類の代表元はすぐに頭に思いついたやつです。)
ここで脊椎動物全体の集合を$X$として、類による部分集合を$X_{1},X_{2}, \ldots ,X_{5}$とおきます。
その上で次のような関係を決めます。
$$x \sim y \overset{def}{\iff} x,yは同じ部分集合X_{i}の元である.(i=1,2, \ldots ,5)$$
これは、同値関係です。(一つの部分集合$Y$だけでもこれは同値関係です。要証明)
この事実から、分類は同値関係$\sim$と代表元で部分集合$X_{i}$を表現できます。
$i=1,2, \ldots , 5$から順に魚・両生・爬虫・鳥・哺乳類として上の代表の生物を利用します。
- $X_{1}=\{y \in X|y \sim マダイ\}=[マダイ]$
- $X_{2}=\{y \in X|y \sim ヒキガエル\}=[ヒキガエル]$
- $X_{3}=\{y \in X|y \sim ヤモリ\}=[ヤモリ]$
- $X_{4}=\{y \in X|y \sim ハチドリ\}=[ハチドリ]$
- $X_{5}=\{y \in X|y \sim アカゲザル\}=[アカゲザル]$
このように、類別の各類が同値関係によって定義される場合に「同値類」と呼ばれます。
実は類別は、どんな部分集合でも同値類の分類と呼べます。
なぜなら、「同じ部分集合の元」が同値関係だったからです。
適当な類別$X=\cup _{i \in I}X_{i}$に対して、$x_{i} \in X_{i}$とすると$X=\cup_{i}[x_{i}]$と表現できます。
これにより、$X$の元は$\{x_{i}|i \in I\}$のただ一つの元と同値になります。
従って、集合$X$は似たもの同士(同値)を同じとしてまとめることができます。
脊椎動物の例だと次のように書けます。
$$X/\sim =\{[マダイ], [ヒキガエル], [ヤモリ], [ハチドリ], [アカゲザル]\}$$
代表系に似ていますが、元はすべて部分集合です。
この同じものを同値関係でまとめてできる集合を「商集合」と呼びます。
このように、どんな類別も同値類の類別だとみなせるので次のことが問題になります。
$$どのような同値関係で類別するか$$
その中でもきれいな同値関係のひとつが整数の割り算でのあまりです。
$$x,y \in \mathbb{Z}に対し, x \sim y \overset{def}{\iff} \exists k \in \mathbb{Z} \; s.t. \; x-y =3k$$
この関係では、$3$で割ったときのあまりで類別されます。
(この場合、同値類は「剰余類」と呼ばれます。)
商集合は$\mathbb{Z}/\sim=\{[0],[1],[2]\}$です。
同値関係をうまく取ることで、再び四則演算を定義できます。
例えば、$Z/\sim$は整数と同じ加法と乗法が定義でき少ない要素で整数について調べられます。
定義 同値類と商集合
それでは、定義していきます。
$X$:集合 $\sim$:$X$の同値関係 $x \in X$
$[x]=\{y \in X|y \sim x\}$:$x$の同値類($\rm{equivalence \; class}$)
$X/ \sim=\{[x]| x\in X\}$:$\sim$による商集合($\rm{quotient \; set}$)
$X/\sim$は等化集合とも呼ばれる.
他の同値類
他の同値類としては、円柱上の線と円周の関係です。
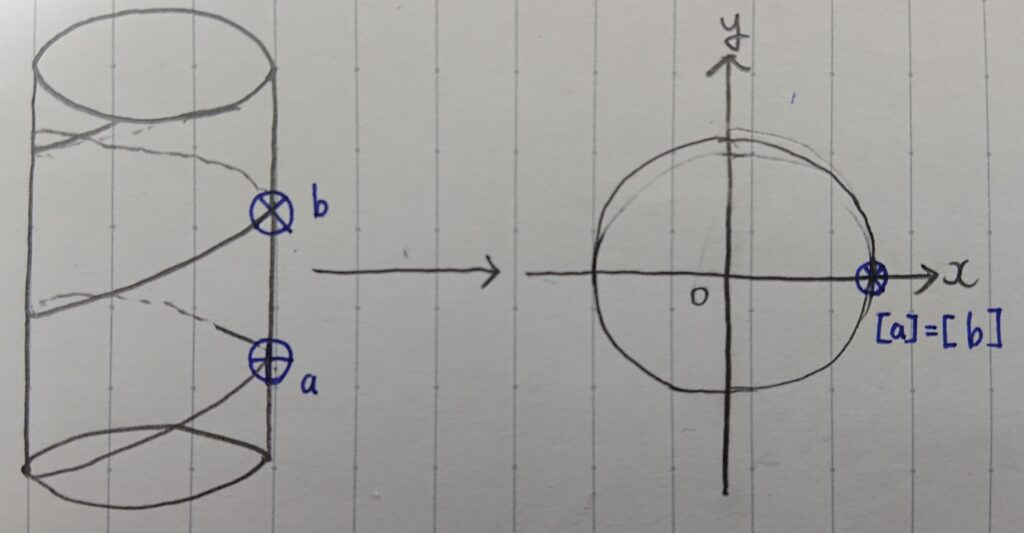
図:円柱上の線と円周
この空間と平面で明らかに違う線になっています。
$P=\{(\cos t,\sin t,t) \in \mathbb{R}|t \in \mathbb{R}\}$を円柱上の線(空間曲線のらせん)
$S^1=\{(\cos t, \sin t) \in \mathbb{R}|t \in \mathbb{R})\}$(平面上の円周)
$P$の元を$X(t)=(\cos t,\sin t,t)$と表します。
しかし、次のような同値関係を考えることで関係が見えてきます。(要確認)
$$a,b \in \mathbb{R}に対して 「X(a) \sim X(b) \overset{def}{\iff} \exists k \in \mathbb{Z}\; s.t. \; a-b =2k\pi」$$
これによって、らせんは$0 \leq t < 2\pi$までの範囲で類別できることになります。
$$X/\sim =\{[X(a)]|0 \leq a < 2 \pi\}$$
このとき、写像$\phi:X/\sim \rightarrow S^1([X(a)] \mapsto (\cos a,\sin a))$が全単射になります。
($X/\sim$の元は代表元の取り方で変わるため、$\phi$のwell-definedを示す必要があります。)
従って、$X/\sim$は$S^1$と同じ集合だとみなせるわけです。
おわりに
同値な元をひとつの類にまとめて、部分集合族を考えることは今回の2種類(整数・円周の例)以外にも存在します。そして、この同値関係の中で重要なものが写像に関する商集合です。写像を全射にすることは、値域を制限することで可能でした。商集合を取る操作は、単射な写像を作ることができます。
この考えに、構造を持つことで代数学における準同型定理となっていきます。
次回は、そんな準同型定理の骨となる「自然な射影」と「誘導写像」を取り扱います。
以上、ケンけんでした。