こんにちは!ケンけんです。今回は、メインのPSTで触れた$\epsilon$近傍によって作られる位相を見ていきます。(結構短め)
それでは行ってみよう!
キーワード:内点と開集合
内点と開集合
$\epsilon$近傍全体が基本近傍系の性質4つを満たす確認の前にまず次の定義を見ておきます。
$\mathbb{R}$を実数全体の集合とする. (加減乗除は利用可)
$A \subset \mathbb{R}$を取る.
$a \in \mathbb{R}$は$A$の内点 $\overset{def}{\iff} \exists \epsilon >0 \; s.t. \; U(a,\epsilon) \subset A$
$A$は開集合$\overset{def}{\iff} \forall x \in A(x:Aの内点)$
これが実数全体集合の位相となります。
一般化した距離空間では、$U(a,\epsilon)$部分が「距離」と言う写像に代わります。
(つまり$\epsilon$近傍の条件「差の絶対値」を取る操作が距離の写像です。)
この定義を見てピコーンときたでしょうか。
実は、位相の構成が近傍系や基本近傍系から作った場合の形になっています。
$$\mathcal{O}(\mathbb{R})=\{A \subset \mathbb{R}|\forall a \in A \exists \epsilon >0 \; s.t. \; U(a,\epsilon) \subset A\}$$
つまり、$\epsilon$近傍全体が近傍または基本近傍系の性質を満たしていることになります。
これを実際に見てみようと言うのが今回の主題です。
証明
近傍系か基本近傍系かで調べることが少し変わりますが、基本近傍系となることが示されます。
$\mathbb{R}$を実数全体の集合とする. (加減乗除は利用可)
各$a \in \mathbb{R}$に対して$\mathcal{N}(x)=\{U(a,\epsilon)|\epsilon >0\}$を取る.
これは, 次の4つの性質を満たし次の位相の基本近傍系となる.
$\rm{(1)}$ $\mathcal{N}(x) \neq \emptyset$,
$\rm{(2)}$ $N \in \mathcal{N}(x) \Rightarrow x \in N$,
$\rm{(3)}$ $\forall N_{1}, \forall N_{2} \in \mathcal{N}(x) \exists N_{3} \in \mathcal{N}(x) \; s.t. \; N_{3} \subset N_{1} \cap N_{2}$,
$\rm{(4)}$ $\forall N_{1} \in \mathcal{N}(x) \exists N_{2} \in \mathcal{N}(x) \forall y \in N_{2} \exists N_{3} \in \mathcal{N}(y) \;s.t. \; N_{3} \subset N_{1}$.
$\rm{(1)}$は明らか($\epsilon=1$としてもよい)なので$\rm{(2)}$以降を示します。
$\rm{(2)}$ 任意の$\epsilon>0$に対し, $U(a,\epsilon)$を取る.
このとき, $0=|a-a|<\epsilon$なので$a \in U(a,\epsilon)$となる.
$\rm{(3)}$ 任意の$\epsilon_{1}, \epsilon_{2}>0$に対し, $U(a,\epsilon_{1}),U(a,\epsilon_{2})$を取る.
今, $\epsilon=\min\{\epsilon_{1},\epsilon_{2}\}>0$を取ると, $U(a,\epsilon) \subset U(a,\epsilon_{1}) \cap U(a,\epsilon_{2})$が成り立つ.
(集合の包含を調べるだけ)
$\rm{(4)}$ 任意の$\epsilon>0$に対し, $U(a,\epsilon)$を取る.
$\epsilon’=\frac{\epsilon}{2}$について, 任意の$y \in U(a, \epsilon’)$を取る.
$a-\epsilon'<y <a$のとき
$\epsilon”=y-a+\epsilon’$に対して$z \in U(y,\epsilon”)$を取る.
このとき, $|z-y|<\epsilon”$より$y-\epsilon” <z<y+\epsilon”$となる.
これは$\epsilon$で$a-\frac{\epsilon}{2}<z<a+\frac{\epsilon}{2}$と表せる.
従って, $|z-a|<\frac{\epsilon}{2} <\epsilon$となり$z \in U(a,\epsilon)$である.
以上から, $U(z,\epsilon”) \subset U(a,\epsilon)$となる.
$a<y <a+\epsilon’$のときは, $\epsilon”=a+\frac{\epsilon}{2}-y$とすることで$U(y,\epsilon”) \subset U(a,\epsilon)$となる.
以上から, $U(a,\epsilon’)$が求める$\epsilon$近傍である.
$\square$
少し開集合を見てみる
さて、基本近傍系によって実数全体に位相を入れましたが、実際のイメージがまだ伴っていません。
そこで少し図を見てみましょう。
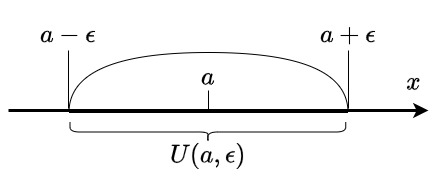
図:$\epsilon$近傍のイメージ図
つまり、点$a \in \mathbb{R}$の$\epsilon$近傍全体は$a$を中心とした幅$\epsilon$の区間を適当に取ったような領域となります。
そして、これは基本近傍系なので各開集合$U_{1}$に対して$U(a,\epsilon) \subset U_{1}$とする$\epsilon$が存在します。
では、極限の定義を振り返りましょう。
$$\forall U=U(a,\epsilon) \in \mathcal{N}(a) \exists N \in \mathbb{N}(n \geq N \Rightarrow a_{n} \in U)$$
これは、$\epsilon$-$N$論法を位相空間の極限らしく書き換えたものでした。
しかし、$\epsilon$近傍全体はどう見ても近傍系全体ではないですね。
(上の図のように正・負の方向に均等に$\epsilon$ずつ広がっていなくても近傍にはなる。)
なのでこのままでは収束を説明できていないように見えます。
そこで、「任意の近傍」と「任意の開近傍」の取り換えが生きてきます。
PST-4導入パートにて次のようなことを挙げています。
- Aさんが属するすべての開集合に属する
- すべてのAさんの近傍に属する
これはPST-2で既に説明しています。
従って、次のように解消されます。
- 任意の$a$の開近傍$U$に対して, ある$U(a,\epsilon)$で$U(a,\epsilon) \subset U$となる,
- ある$N \in \mathbb{N}$で$n \geq N \Rightarrow a_{n} \in U(a,\epsilon) \subset U$
- 従って, 任意の$\epsilon$近傍を考えることで任意の開近傍についても成立する.
数列の極限の定義は、このような論理が隠れていたわけですね。
(これじゃあ、大学一年で論理をしっかり学ぶ前だと暗記するしかないなと。)
おわりに
実は今回の記事(とPST-3’)を書くにあたって初めて数列の極限の構成の意味と正しさを見ました。何よりも、実数の位相が基本近傍系から構成されていることもです。
一般の位相空間に入ると大体距離空間(と実数の位相など)との関係をしっかり議論する時間がなく軽視されがちです。極限も距離空間で大体止まってしまうのでなおさらでしょう。
正直、内点の見え方が書く前後で一気に変わりました。
以上、ケンけんでした。