こんにちは!ケンけんです。今回は、「絶対に理解するHom関手」の第2弾です。
内容としては、Hom関手と完全列との関係です。完全列に初めて触れた後すぐに話題として上がるHomの完全列を取り扱いますよ。(個人的恨みつらみが溜まった命題)
それでは行ってみよう!
キーワード:Hom関手の左完全性
この記事の続きです。
この記事では環はすべて単位的可換環とします。
完全列の復習
とは言え、まずは完全列の復習をしておきます。
$\{L_{i}\}_{i \in I}$を$R$-加群の族と各$i \in I$で$R$-線形写像$f_{i}:M_{i} \rightarrow M_{i-1}$を取り次の列$l$を考える.
$$l:\cdots \rightarrow M_{i-1} \overset{f_{i-1}}{\rightarrow} M_{i} \overset{f_{i}}{\rightarrow} M_{i+1} \rightarrow \cdots $$
$l$は$R$-加群の完全列である $\overset{def}{\iff} \forall i \in I(\mathrm{Ker}f_{i+1}=\mathrm{Im}f_{i})$
$\mathrm{Ker}f_{i+1}=\mathrm{Im}f_{i}$のとき, $M_{i}$は完全と呼ぶ.
(つまり、$l$が完全列とは、各$i \in I$で$M_{i}$が完全とも定義できる.)
このように、一つの加群を挟む線形写像の$\mathrm{Im},\mathrm{Ker}$の関係を表したものです。完全列の証明では、核が像の部分集合であることがよく問題となります。この簡単な包含条件を満たす加群の列が、前回挙げたホモロジーを定義する鎖複体と呼ばれるものになります。
また、両端が$0$加群の場合はとても単純で短完全列と呼ばれます。
- $0 \overset{p}{\rightarrow} M$は$p$を零写像
- $M \overset{q}{\rightarrow} 0$は$q$を零写像
また、今回は示しませんが次のことも成り立ちます。
- $0 \rightarrow L \overset{f}{\rightarrow} M$は完全 $\iff f$は単射
- $M \overset{g}{\rightarrow} N \rightarrow 0$は完全 $\iff g$は全射
自明な完全列としては次のような例があります。(前の記事の完全列の一般化)
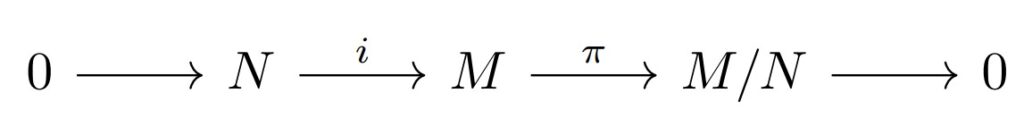
- $R$-加群$M$とその部分加群$N$
- 包含写像$i$(単射)・自然な準同型$\pi$(全射)
主題の完全性とは、次の性質です。
「与えられた完全列の加群を写像(実際には関手)で写したもので考えても完全列になる。」
左や右の差が出るのはこれから考えます。
Hom関手 左完全性
さて、今回の主題は何度も$\mathrm{Hom}_{R}(-,-)$を書くためこれを省略記号で次のように書きます。
$M,P$を$R$-加群とする.
$\mathrm{Hom}_{R}(M,P)=M^{P},\mathrm{Hom}_{R}(P,M)=M_{P}$
これは、$*$付き写像の上付き・下付きと対応するように取っています。
例えば、$M^{P}$と$f \in \mathrm{Hom}_{R}(L,M)$を考えると$f^{*}:M^{P} \rightarrow L^{P}$です。
それでは本題の命題を見ていきましょう。
次の$R$-加群の列$l_{1},l_{2}$を考える.
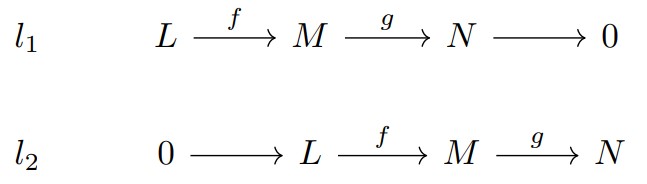
このとき次のことが成り立つ.
$\rm{(1)}$ $l_{1}$は完全列 $\iff \forall P :R$-加群 $(l^{*}:0 \rightarrow N^{P} \overset{g^{*}}{\rightarrow} M^{P} \overset{f^{*}}{\rightarrow} L^{P}:$完全列$)$
$\rm{(2)}$ $l_{2}$は完全列 $\iff \forall P :R$-加群 $(l_{*}:0 \rightarrow L_{P} \overset{f_{*}}{\rightarrow} M_{P} \overset{g_{*}}{\rightarrow} N_{P}:$完全列$)$
実はこの主張の半分は既に前回の命題4(参照 命題4)によって示されています。
今の記号で書くと、次のようになっています。
- $\rm{(1)}$では, $N$は完全 $\iff g$は全射 $\iff g^{*}$は単射 $\iff N^{P}$は完全
- $\rm{(2)}$では, $L$は完全 $\iff f$は単射 $\iff f_{*}$は単射 $\iff L_{P}$は完全
従って、示すべきことは任意の$P$についてそれぞれ次のことになります。
それでは示していきます。
($\Rightarrow$) $l_{1}$が完全であると仮定し, 任意の$R$-加群$P$を取る.
(その1 命題4より)$g$が全射より$g^{*}$は単射である.
(その1 命題3より)$f^{*} \circ g^{*}=(g \circ f)^{*}=(0)^{*}=0$である.
従って, $\mathrm{Im}g^{*} \subset \mathrm{Ker}f^{*}$より逆の包含を示せば十分である.
任意の$p \in \mathrm{Ker}f^{*}$を取ると, $f^{*}(p)=p \circ f=0$である.
従って, $\mathrm{Ker}g=\mathrm{Im}f \subset \mathrm{Ker}p$となる.
自然な準同型$\pi:M \rightarrow M/\mathrm{Im}f$に対して, $p$から一意的に$\tilde{p}:M/\mathrm{Im}f \rightarrow P$を誘導する.
また, 準同型定理より, $M/\mathrm{Im}f=M/\mathrm{Ker}g \cong N$である.
これは, $g$から誘導される写像で$\tilde{g}: M/\mathrm{Im}f \rightarrow N$として与えられる.
従って, $\psi=\tilde{p} \circ (\tilde{g})^{-1}$によって次の可換図式が得られる.

以上より, $p=\tilde{p} \circ \pi=\psi \circ (\tilde{g} \circ \pi)=\psi \circ g=g^{*}(\psi) \in \mathrm{Im}g^{*}$である.
($\Leftarrow$) 任意の$R$-加群$P$について$g^{*}$が単射より, $g$は全射である.
$l^{*}$の完全性から$(g \circ f)^{*}=f^{*} \circ g^{*}=0$である.
今$P=N$を取ると, $(g \circ f)^{*}(\mathrm{id_{L}})=g \circ f=0$となる.
従って, $\mathrm{Im}f \subset \mathrm{Ker}g$であり逆の包含を示せば十分である.
自然な準同型$\pi:M \rightarrow M/\mathrm{Im}f$に対し, $P=M/\mathrm{Im}f$で$\pi \in \mathrm{Ker}f^{*}=\mathrm{Im}g^{*}$である.
従って, ある$k \in N^{P}$により$\pi=g^{*}(k)=k \circ g$と表せる.
従って, $\mathrm{Im}f=\mathrm{Ker}\pi \supset \mathrm{Ker}g$である.
$\square$
$\rm{(2)}$は、考え方が同じのため要点だけ書いていきます。
($\Rightarrow$) $l_{1}$が完全であると仮定し, 任意の$R$-加群$P$を取る.
- (その1 命題4より)$f$が単射より$f_{*}$は単射,
- (その1 命題3より)$(g \circ f)_{*}=g_{*} \circ f_{*}=0$で$\mathrm{Im}f_{*} \subset \mathrm{Ker}g_{*}$,
- $h \in \mathrm{Ker}g_{*}$について$g_{*}(h)=g \circ h=0$,
- よって, $\mathrm{Im}h \subset \mathrm{Ker}g=\mathrm{Im}f$,
- $f$の単射性から準同型定理で, $L \cong \mathrm{Im}f$,
- $h$の値域を制限し$h’:P \rightarrow \mathrm{Im}h$を取る,
- $h’$, 包含写像$i:\mathrm{Im}h \rightarrow \mathrm{Im}f$, 同型写像$\phi:\mathrm{Im}f \rightarrow L$を合成,
- 写像の一致から$h=f \circ (\phi \circ i \circ h’)=f_{*}(\phi \circ i \circ h’)$,
- $\phi \circ i \circ h’ \in L_{P}$より, $h \in \mathrm{Im}f_{*}$.
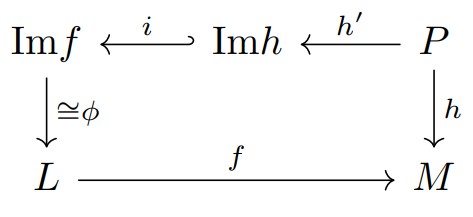
図:考えていた可換図式
($\Leftarrow$) 任意の$R$-加群$P$について$f_{*}$が単射より, $f$は単射である.
$P=L$とする.
- $l_{*}$の完全性より$(g \circ f)_{*}=g_{*} \circ f_{*}=0$,
- $\mathrm{id}_{L}$について$g \circ f =(g \circ f)_{*}(\mathrm{id}_{L})=0$
- よって, $\mathrm{Im}f \subset \mathrm{Ker}g$.
$P=\mathrm{Ker}g$とする.
- 包含写像$i:\mathrm{Ker}g \rightarrow M$について, $g_{*}(i)=g \circ i=0$,
- $\mathrm{Im}f_{*} = \mathrm{Ker}g_{*}$よりある$k \in L_{P}$が存在し, $i=f_{*}(k)=f \circ k$,
- $x \in \mathrm{Ker}g$について$x=i(x)=(f \circ k)(x)=f(k(x)) \in \mathrm{Im}f$である.
以上から, $\mathrm{Ker}g=\mathrm{Im}f$である.
$\square$
方針の箇条書きにしてみました。
今、$\mathrm{Hom}_{R}(-,P),\mathrm{Hom}_{R}(P,-)$の圏論的な性質「左完全性」を示しました。完全性は、加群の「圏」独特の性質でありいよいよ「$\mathrm{Hom}$」を考えるのに圏論の言葉を避けて通るのは難しくなりそうです。
圏と関手は次回に回すとして、左完全の形が図式的に意味することを書いておきます。
完全列「$0 \rightarrow L \rightarrow M \rightarrow N$」について関手$F$が左完全であるとは、
$$0 \rightarrow F(L) \rightarrow F(M) \rightarrow F(N)$$
が完全列となることです。$\mathrm{Hom}_{R}(P,-)$がこれに該当します。
$l_{2}$と$F’=\mathrm{Hom}_{R}(-,P)$では、「$0 \rightarrow F'(N) \rightarrow F'(M) \rightarrow F'(L)$」でも左完全なのか?となります。これは、$\mathrm{Hom}_{R}(-,P)$と$\mathrm{Hom}_{R}(P,-)$の関手としての写し方が違うからです。
今回は文献[1]では、($\Leftarrow$)も証明していましたが実際には($\Rightarrow$)の方だけで情報は十分なのか他の文献では($\Rightarrow$)だけ考えています。これも、$\mathrm{Hom}$を関手として考えるなら納得できます。
なぜ短完全列で考えないのか?
先の命題を考えると、なぜ短完全列で考えないのか?と考えると思います。
短完全列の場合、次のことを追加で示す必要があります。
- $l_{1}$について「$f:L \rightarrow M$」は単射 $\iff$ 「$f^{*}:M^{P} \rightarrow L^{P}$」は全射
- $l_{2}$について「$g:M \rightarrow N$」は全射 $\iff$ 「$g_{*}:M_{P} \rightarrow N_{P}$」は全射
果たしてこんなことが言えるのでしょうか。この主張について反例が存在しました。
しかも、以前の記事で採用した完全列です。
1.の反例はすぐに出せます。
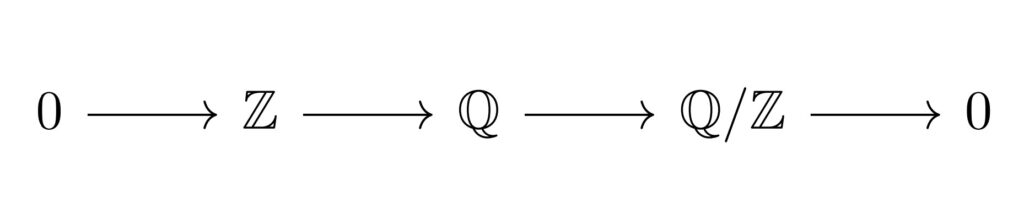
図:短完全列(divisible module 情報保存の反例)
$P=\mathbb{Z}$として, $\mathbb{Z}^{P}\neq 0, \mathbb{Q}^{P}=0, (\mathbb{Q}/\mathbb{Z})^{P}=0$となる.
以上から, 「$0=\mathbb{Q}^{P} \rightarrow \mathbb{Z}^{P}$」は全射になり得ません。
2.の反例は少し単純化した次の列です。
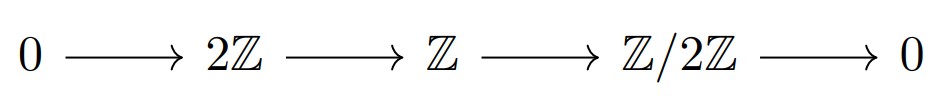
図:短完全列(torsion-free module 情報保存の反例)
$P=\mathbb{Z}/2\mathbb{Z}$として, $(2\mathbb{Z})_{P}=0, \mathbb{Z}_{P}, P_{P} \neq 0$です。
こちらは比較的単純なので$\mathrm{Hom}_{R}(P,2\mathbb{Z}) =(2\mathbb{Z})_{P}=0$を確かめます。
- $\phi \in \mathrm{Hom}_{R}(P,2\mathbb{Z})$について$\phi(0+2\mathbb{Z})=0$,
- $1+2\mathbb{Z}$について, $\phi (1+2\mathbb{Z}) =k$と仮定,
- $0=\phi(0+2\mathbb{Z})=\phi(1+2\mathbb{Z})+\phi(1+2\mathbb{Z})=2k$,
- 従って, $k=0$で$\phi=0$で, $(2\mathbb{Z})_{P}=0$である.
($\mathbb{Q}^{P}=0, (\mathbb{Q}/\mathbb{Z})^{P}=0$の証明はdivisible moduleの話になるのでまた単独で扱います。)
このように、単純な例で反例を作ることができてしまいます。
おわりに
当初苦しめられた命題が、今ではそれほど苦もなく示すことができるようになり自身の成長が感じられました。また、ずっと考えていた完全列の反例が今回利用でき話のつながりを実感します。
(そのせいで、divisible moduleの話がわいてきましたが…)
今回は左完全性の話でしたが、(その3)はいよいよ圏(特に加群の圏に絞って)を取り扱い、今回までの定義と言葉を見直して行きます。
以上、ケンけんでした。
参考文献
[1]M.F.Atiyah; I.G.MacDonald, Introduction to Commutative Algebra,Addison-Wesley Publishing Company, London (1969)