こんにちは!ケンけんです。今回は以前の記事で保留した$\rm{torsion}$-$\rm{free \; module}$と$\rm{divisible \; module}$についての完全列の情報保存を解決するための手段の一つとして「Five Lemma」を扱います。
そして、実は$\rm{torsion}$-$\rm{free}$と$\rm{divisible}$では情報保存が不完全であることがわかったのでそれも解説します。
(情報保存とは何かについてはここからからどうぞ)
それでは行ってみよう!
キーワード:Five Lemma(5項補題)
この記事では環はすべて単位的可換環とします。
Five Lemma
まずは相手を知り証明しましょう。
行が完全列となっている次の$R$-加群の可換図式を考える.
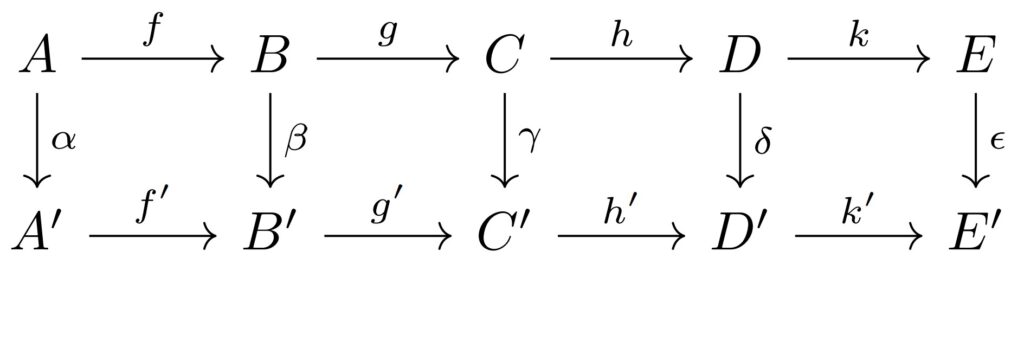
このとき, 次のことが成り立つ.
$\rm{(1)}$ $(\beta, \deltaは単射) \wedge (\alphaは全射) \Rightarrow \gammaは単射$
$\rm{(2)}$ $(\beta, \deltaは全射) \wedge (\epsilonは単射) \Rightarrow \gammaは全射$
どちらも長くわかりにくいため、証明ブロックを分割していきます。
$\gamma$の単射性は$\mathrm{Ker}\gamma \subset \{0_{C}\}$を示せば十分である.
任意の$c \in \mathrm{Ker}\gamma$を取ると, $\gamma(x)=0_{C’}$である.
可換性$h’ \circ \gamma =\delta \circ h$から, $0_{D’}=h'(\gamma(c)) =\delta (h(c))$である.
$\delta$の単射性より, $h(c)=0_{D}$となるため$c \in \mathrm{Ker}h=\mathrm{Im}g$である.
よって, ある$b \in B$によって$c=g(b)$である.
可換性$g’ \circ \beta = \gamma \circ g$から, $g'(\beta(b))=\gamma(g(b))=\gamma(c)=0_{C’}$である.
従って, $\beta(b) \in \mathrm{Ker}g’=\mathrm{Im}f’$からある$a’ \in A’$により$\beta(b)=f'(a’)$である.
$\alpha$は全射なので, ある$a \in A$によって$a’=\alpha(a)$である.
可換性$f’ \circ \alpha = \beta \circ f$から, $\beta(b)=f'(\alpha(a))=\beta(f(a))$である.
$\beta$の単射性と$\beta(b-f(a))=0_{B’}$から$b=f(a) \in \mathrm{Im}f=\mathrm{Ker}g$である.
以上から, $c=g(f(a))=0_{C}$となり$\mathrm{Ker}g \subset \{0_{C’}\}$である.
$\square$
任意の$c’ \in C’$を取り$h'(c’)$を考える.
$\delta$の全射性より, ある$d \in D$によって$h'(c’)=\delta(d)$である.
可換性$k’ \circ \delta = \epsilon \circ k$から, $0_{E’}=k'(h'(c))=k'(\delta(d)) = \epsilon(k(d))$である.
$\epsilon$の単射性から, $k(d)=0_{E}$となるため$d \in \mathrm{Ker}k=\mathrm{Im}h$である.
よってある$c \in C$により$d=h(c)$と表せる.
可換性$h’ \circ \gamma =\delta \circ h$より, $h'(\gamma(c)) =\delta(h(c))=\delta(d)=h'(c’)$である.
$h'(\gamma(c)-c’)=0_{D’}$より$\gamma(c)-c’ \in \mathrm{Ker}h’=\mathrm{Im}g’$である.
よってある$b’ \in B’$により, $\gamma(c)-c’=g'(b’)$である.
$\beta$の全射性から, ある$b \in B$によって$b’=\beta(b)$と表せる.
可換性$g’ \circ \beta = \gamma \circ g$から, $\gamma(c)-c’=g'(b’)=g'(\beta(b))=\gamma(g(b))$となる.
以上から, $\gamma(c-g'(b))=c’ \in \mathrm{Im}\gamma$となり$\gamma$は全射である.
$\square$
証明のステップ部分でどこの可換性を利用しているのか太字にしてわかりやすくしています。
さて、この命題を利用すると次の短完全列版がすぐに求まります。
行が完全列となっている次の$R$-加群の可換図式を考える.
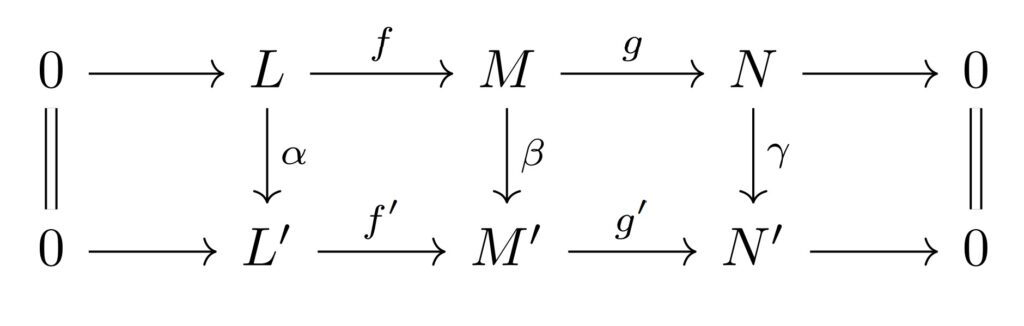
このとき, 次が成り立つ.
$\rm{(1)}$ $(\beta, \deltaは単射) \Rightarrow \gammaは単射$
$\rm{(2)}$ $(\beta, \deltaは全射) \Rightarrow \gammaは全射$
命題1での両端部分$\alpha, \epsilon$が恒等写像$\mathrm{id}$となっているので全単射です。従って, 系での図における真ん中を挟んだ$\alpha, \gamma$のみ考えれば十分になり仮定側が簡略化されます。
(なので証明は命題1からすぐに従います。)
やっと前回の課題へ
さてこのFive Lemmaによって次のように考えることで$\rm{torsion}$-$\rm{free}$, $\rm{divisible}$について一方向は示すことができます。
$0 \rightarrow L \overset{f}{\rightarrow} M \overset{g}{\rightarrow} N \rightarrow 0$を$R$加群の完全列とする.
$\rm{(1)}$ $L,Nは\rm{torsion}$-$\rm{free}である\Rightarrow$ $Mは\rm{torsion}$-$\rm{free}である$,
$\rm{(2)}$ $L,Nは\rm{divisible}である\Rightarrow$ $Mは\rm{divisible}である$.
$\rm{(1)}$仮定より, 任意の$r \in \mathrm{Reg}_{R}R$に対し$r$倍写像$r_{L}:L \rightarrow L, r_{N}:N \rightarrow N$は単射である.
従って, 次の可換図式を考えると, 系2 $\rm{(1)}$から$r_{M}:M \rightarrow M$が単射である.
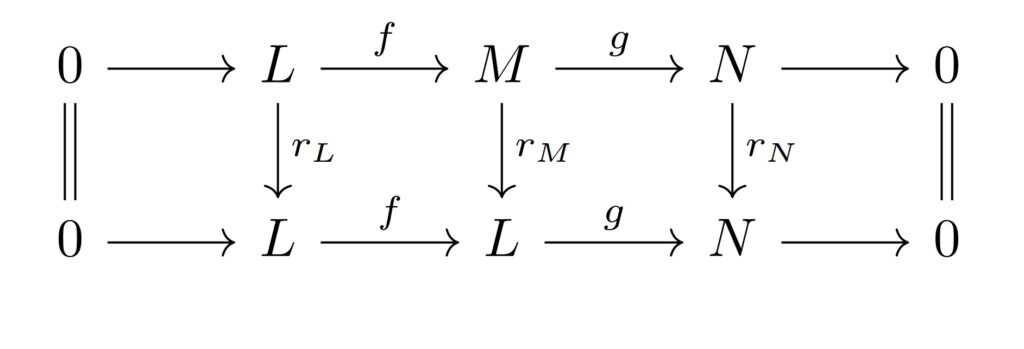
よって, $M$は$\rm{torsion}$-$\rm{free}$である.
$\rm{(2)}$仮定より, 任意の$r \in \mathrm{Reg}_{R}R$に対し$r$倍写像$r_{L}:L \rightarrow L, r_{N}:N \rightarrow N$は全射である.
従って, 先ほどと同じ可換図式を考えると, 系2 $\rm{(2)}$から$r_{M}:M \rightarrow M$が全射である.
よって, $M$は$\rm{divisible}$である.
$\square$
あれ?逆はどうなのと思ったことでしょう。私は前回の記事を書いた段階では成り立つと思っていたのですが、どうも証明できませんでした。そこでちょっとした例を考えると反例を見つけてしまったのです。
$\rm{divisible}$の場合
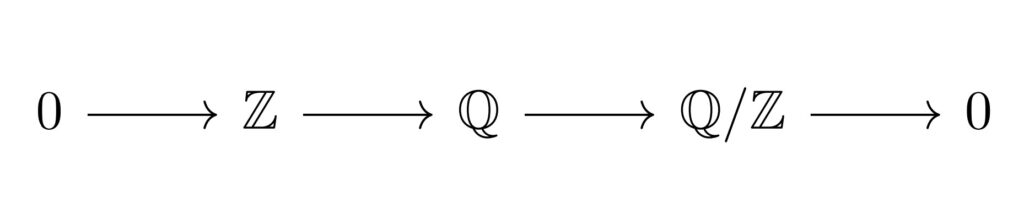
図:$\rm{divisible}$の反例となる完全列
これは自明は完全列$0 \rightarrow N \overset{i}{\rightarrow}M \overset{\pi}{\rightarrow} M/N \rightarrow 0$($i$は包含写像, $\pi$は自然な準同型)として$\mathbb{Z}$-加群で考えたものです。
そうすると、有理数はいくらでも分母・分子に同じ整数をかけることができるため$\mathbb{Q}$とその剰余加群$\mathbb{Q}/\mathbb{Z}$については全射となります。
しかし、有理整数環$\mathbb{Z}$はどうやっても全射にできません。例えば、$r=2$とする場合$2x=1$とするような$x \in \mathbb{Z}$は取れません。従って、$\mathbb{Z}$は$\rm{divisible}$ではありません。
$\rm{torsion}$-$\rm{free}$の場合
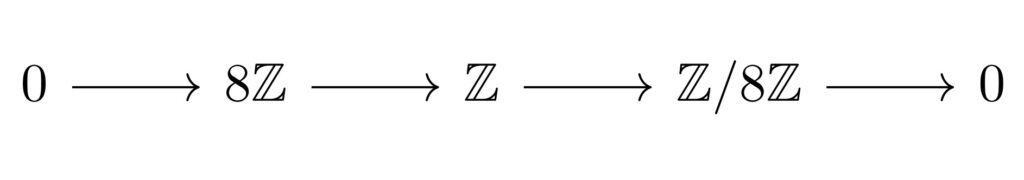
図:$\rm{torsion}$-$\rm{free}$の反例となる完全列
先ほどと同様に自明な完全列を取ったものでこれも$\mathbb{Z}$-加群として取っています。このとき、$8\mathbb{Z}$と$\mathbb{Z}$が$r$倍写像で単射になることは係数部分を割る操作からわかります。
($x, y \in \mathbb{Z}$において$2x=2y$ならば$x=y$とするように。)
しかし剰余加群$\mathbb{Z}/8\mathbb{Z}$においては$r=8$の場合単射ではなくなります。
$8(\mathbb{Z}/8\mathbb{Z})=\{0+8\mathbb{Z}\}$なのでどうやっても単射になりません。
以上のように、整域で反例を見つけてしまったのでした。$\rm{torsion}$の場合は「~が存在する」と言う条件だったため単射・全射のいいとこどりができましたが、$\rm{torsion}$-$\rm{free}$, $\rm{divisible}$では「任意の正則元」と言う強い条件がかなり悪さをしているようです。
直接証明から見る複雑さ
今回はFive Lemmaを使ってスマート?に解きましたが、実は裏で直接証明もできました。その時感じたことが、$\rm{torsion}$の時と比べて必要な情報が多いと言うことです。
前回の記事で完全列の情報保存の証明では次の2つに分かれていると考察していました。
- 隣接する加群については短完全による単射性と全射性を利用
- 真ん中の加群についてはその加群での完全性を利用
今回は2つ目の真ん中の加群について考察します。
2つとも書くと長くなるの$\rm{torsion}$-$\rm{free}$だけ書きます。
$r \in \mathrm{Reg}_{R}R$について$rm=0_{M}$とする$m \in M$を取る.
このとき, $g(rm)=rg(m)=0_{N}$である.
$N$は$\rm{torsion}$-$\rm{free}$より$r$倍写像は単射で$g(m)=0_{N}$である.
従って, $m \in \mathrm{Ker}g=\mathrm{Im}f$からある$l \in L$によって$m=f(l)$と表される.
$rm=0_{M}$より$0_{M}=rm=rf(l)=f(rl)$となり$rl \in \mathrm{Ker}f$である.
ここで$f$は単射より$rl=0_{L}$である.
$L$は$\rm{torsion}$-$\rm{free}$より$r$倍写像は単射で$l=0_{L}$である.
以上から, $m=f(l)=0_{M}$で$M$における$r$倍写像は単射より$M$も$\rm{torsion}$-$\rm{free}$である.
$\square$
$\rm{torsion}$の場合と明確に違う部分を太字にしました。そう、$f$の単射性が必要になっているんです。本当に一行だけですがそれでも$\rm{torsion}$よりも情報として必要なことが増えています。つまり前回考察した「真ん中の加群についてはその加群での完全性を利用」が破綻してしまっています。このような証明に必要な情報を考えるだけで逆方向の証明ができるなら余計な情報が必要(もしくはそもそも証明できない)だと予想できます。
ちなみに$\rm{divisible}$の方は$g$の全射性が必要でした。
そしてこの対応、先ほどの反例を見ると納得します。
$\rm{divisible}$の場合
$\mathbb{Z}/\mathbb{Q}$は$\rm{divisible}$でしたが、$\rm{divisible}$では$\pi:\mathbb{Q} \rightarrow \mathbb{Z}/\mathbb{Q}$の全射性が必要でした。
$\rm{torsion}$-$\rm{free}$の場合
$8\mathbb{Z}$側は$\rm{torsion}$-$\rm{free}$でしたが、$\rm{torsion}$-$\rm{free}$では$i : 8\mathbb{Z} \rightarrow \mathbb{Z}$の単射性が必要でした。
このように、反例でも証明に必要な部分ではうまくいっているのです。こうやって証明を見比べることでも反例との対応を考えられていいですね。
おわりに
まさか$\rm{torsion}$-$\rm{free}$と$\rm{divisible}$ではうまくいかないとは…でも今回の記事ではいろいろ勉強になりました。
Five Lemmaを自力でしっかり証明したのは実ははじめてだったりします。(snake Lemmaは示したことがある。初見時すっごい苦しめられた。)ですが、可換図式と完全列の性質を利用した強い主張なのでよい練習になると思います。
また、証明がうまくいかないと気付いた段階で前回の証明の特徴に着目してそれに沿う反例を作ると言うのも有効であるとわかりました。
前後編と言う形になりましたが、納得のいく成果が得られて満足です。
以上、ケンけんでした。 ではでは~
(次のMOD-Lは$\mathrm{Hom}$関手第2弾だと思います。)