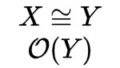こんにちは!ケンけんです。今回は、位相空間の基本「位相」を取り扱います。
キーワード:位相
いきなり定義 位相
まず、相手を知ることから始めましょう。いきなり位相の定義から入ります。
$X$:集合 $\mathcal{O}(X) \subset 2^{X}$ $I$:添字集合 $i \in I$
- $\emptyset, X \in \mathcal{O}(X)$,
- 任意個の$X_{i} \in \mathcal{O}(X)$について$\cup X_{i} \in \mathcal{O}(X)$,
- $Y, Z \in \mathcal{O}(X) \Rightarrow Y \cap Z \in \mathcal{O}(X)$
$\mathcal{O}(X)$は$X$の位相($\rm{topology}$) $\overset{def}{\iff} \mathcal{O}(X)は1.2.3.を満たす$
$\mathcal{O}(X)$の元を$X$の開集合($\rm{open \; set}$)と呼ぶ.
$(X,\mathcal{O}(X))$を位相空間($\rm{topological \; space}$)と呼ぶ.
私たちは今、命題論理と集合・写像の知識のみだと言う前提があります。そうなると何か新しいことを考える際には、違う言葉を作るか既存の道具を使って説明できる対象を考えるかです。今回は後者で、集合の共通部分・和集合・空集合を定義の中に持っていますね。
さて、早速何が起こっているかわかりません。「確かに知ってる道具使って定義してるけど、何がしたいの?」と思うでしょう。一般の位相空間論の講義では(多分)距離空間から始まって途中で位相空間に一般化していくことが多いです。でも、なぜ位相の定義がこうなのかを深くは考えないでしょう。下手すると距離空間の位相がどんなものか議論せずに終わる講義だってありそうです。
しかし、この摩訶不思議な定義もしっかり近さをとらえていると言えます。それを考えるためにちょっとした図示をして考えましょう。
位相の図示?
位相は集合の元の間で近さを測る物差しであると初回に説明したと思います。そして私はこの近さを人間関係と見れば説明がつくと言う結論を得ました。
まず、AさんとBさんを中学生か高校生で兄弟であり、それぞれ次の趣味や特性を持つ想定します。
- Aさん(弟)
- 化学が大好きで構造式集のような本を見るのが趣味
- スポーツは得意ではないが水泳とウォーキングは好き
- 一時期ゲームばかりやっていたせいで目が悪い。
- 絵を描くのが好きで美術部所属である。
- Bさん(兄)
- 数学に興味を持ち始めている。よく図書館にこもってる。
- スポーツは普通、団体行動は好きではないがそれなりに妥協できる。
- 騒がしい場所が苦手
- 文章を書いたり更生したりするのが好きで新聞委員である。
こんな特性と持っていたとしましょう。すると、ここから人間関係が生えてきます。まず、自分自身と単純な関係としては兄弟関係の2つが既にあります。
次にAさんの化学好きから、他の「科学」好きな同級生と一緒に図書館で調べものをしたり、一緒に博物館に行ったりする仲があるかもしれません。ここに、科学好きの関係があります。
Bさんは妥協はできるが騒がしい場所が苦手なので学校行事では静かな(保健室代わりの部屋とかテントとか)でじっとして休憩していることが多いです。その時に、同じように音に敏感な生徒や体調を崩しやすい生徒が落ち着くためにやってきます。そうするといつも同じメンツが使っているなんてことがありえます。音に敏感だとかすぐに体を壊すと言った特性から顔見知りになったりします。ここにも人間関係ができます。
他にも、新聞委員で一緒に仕事をする相方との関係や、水泳でスクールに通っていると同級生で同じクラスに所属しており、よく話すといったような関係もあり得ます。AさんBさんの中の情報だけでこれだけ関係が出せます。
次に、Aさんの科学関係を経由してBさんの数学でのつながりがある人がいるかもしれません。また、音などに弱くていつも顔を合わせる人の中には新聞委員の相方が持っている小説などの情報共有の関係の一人かもしれません。その関係の中にはAさんBさんが全く関わりのない人もいるかもしれません。
こんな風に起点は二人の関係ですが、ちょっとした関係からどんどん人間関係は広がっていきます。でも、これはすべて学校の中での関係で閉じていますね。図で書くと次のようなイメージです。
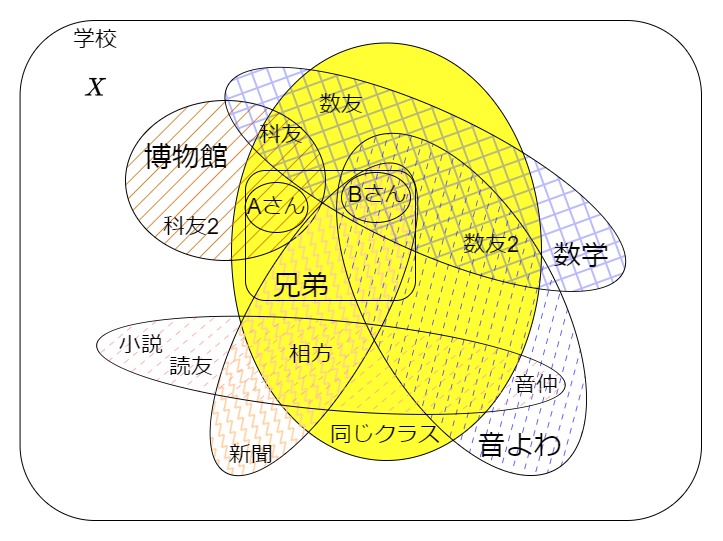
図:AさんBさん、その周りの人間関係の図
実際にはもっとたくさんの関係があると思いますが今回はこれくらいで十分でしょう。上の図がまさしく位相の図示となっているのです。
人間関係は位相か?
では、本題の位相に戻ります。実は先の例でもう位相が構成できています。おまけに近さについても説明できます。
1.位相になっている?
まず人間関係は、学校と言う生徒の集まり$X$の中で閉じており特定の特性ごとに集まった生徒です。なのですべて部分集合です。
次に、$\mathcal{O}(X)$の基準として「$P(X_{i})$:$X_{i}$はAさんとBさんを含む人間関係により決まる集合」または「$Q(X_{i})$:$X_{i}$はAさんBさんを含まないがAさんBさんと関係を持つ人を含む人間関係により決まる集合」と言う風に制限します。これがまさしく上の図の形になっています。集合として書くと次のようになります。
$$\mathcal{O}(X)=\{Y \in 2^{X}|P(Y) \vee Q(Y)\}$$
1.の条件を見てみましょう。
- 空集合$\emptyset$:何も関係がない集合(何も関係を持っていない)
- 全体集合$X$:学校全体(ある種同じ学校に通っていると言う関係)
確かに、$\mathcal{O}(X)$の条件を満たしていますね。
2.の条件を見てみましょう。
$\mathcal{O}(X)$の元$X_{i}$を任意個で和集合を考えて$\mathcal{O}(X)$の条件を満たさないとはどういうことでしょう。命題の否定を考えると、「AさんBさんの関わりの無い人の人間関係」かつ「その人の関係の中にAさんとBさんがいない」です。しかし、和集合$\cup_{i} X_{i}$でできる人間関係に属する生徒は少なくともある人間関係$X_{i}$に属することになる。そうすると、和集合でできる人間関係の属する人も少なからずAさんBさんに関わりがあるかその知人と関係を持っていることになります。従って、$\cup_{i} X_{i} \in \mathcal{O}(X)$です。当然、上の絵での〇で囲まれている部分すべてがそうです。
最後に3.の条件を見てみましょう。
そうすると空集合になるケースがありますね。それは$Y,Z$に属する生徒はAさんBさんと関係があるが、$Y,Z$で互いに全くかかわりがないケースである。先ほどの絵を見ると、科学つながりの生徒と小説つながりの生徒では関係を持っていません。そうです、「関係を持っていません」。なので、$\emptyset$としていいわけです。$\emptyset$ではない場合は、$Y,Z$の中でAさんBさんと直接関係があるか、関係がある人を介して同じ人間関係に属していると言うことになります。先の絵で見ると「相方さん」や「音仲さん」などが該当します。また、絵で考えるなら〇で何重にも囲まれている個所がまさしく共通部分です。つまり、上の図はベン図だと言えます。
以上から、上の例は位相の定義を満たしていることになります。
2.任意個と2つの差は?
ではなぜ和集合は任意個なのに共通部分は2個だけなのでしょう。それは和集合ではどんなに頑張って$X_{i} \subsetneq X$をとっても$X$にならない場合があるからです。上の図だと、〇で囲まれていない領域がありますね。簡略化と言う意味もありますが、全くAさんBさんとその周辺の知人とも人間関係がない生徒があり得ます。
例えば、学年が違う上に同じ部活や委員会に所属していないと言った生徒だと関わる機会自体がほとんどあり得ません。そうなると、同じ学校に通っていることぐらいしか関係ありません。しかし、共通部分だと、先の3.番の検証の時点で空集合$\emptyset$を構成できています。そうなるとどんな集合を追加で共通部分を考えても空集合なので考える必要が無くなります。
従って、2つの共通部分を指定するだけで十分になってしまうのです。このように、$X$と$\emptyset$の「作れる」か「作れるかわからない」の大きな差が位相の定義に影響を与えているとわかります。
3.どこが近さに?
近さはまさに人間関係です。これは特定の趣味や特性が「近い」からできるものです。例えば、Aさんを中心に何重にも関係が重なる人はとてもAさんに似たそっくりさんだとわかります。逆に、関係の重なりが弱い人は同じ学校に属しているだけの生徒です。Bさんについても同じです。
つまり、こういうことです。
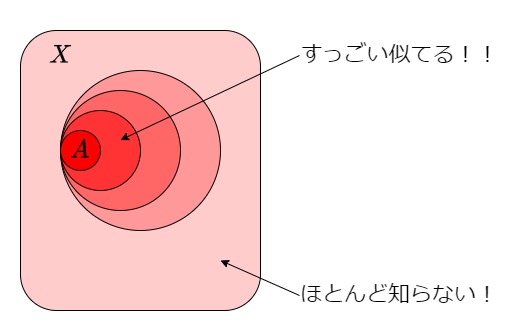
図:Aさんに近い人・遠い人
共通部分だけで近いかどうかがわかる、集合論の言葉だけで説明できる素晴らしい手法です。
おわりに
いかがでしたでしょうか?実は、今回の解釈やイメージは別の記事を書くために試行錯誤した結果です。下手に、長さや距離の発想があるせいで位相本来のモチベーションが失われがちですが、今回集合だけで「近さ」を作るにはどうすればいいか?の姿勢を取ることでただ暗記するよりも納得できると思います。位相空間に苦しむ方の参考になれば幸いです。
次回は、位相並みに実は重要な「近傍」を取り扱います。
以上、ケンけんでした。