(2024/2/7 更新しました!)
こんにちは!ケンけんです。
前回は、2つの集合の間の写像が逆方向の写像(逆写像)を持つ全単射を取り扱いました。
今回は、それを緩めた単射や全射を取り扱います。
キーワード:単射・全射
導入
単射編
さんざん使われた秀吉の例ですが、今回も利用します。
前回、数の不明なものは全単射によって数量がわかるものと一対一対応(全単射)させることで数量がわかるとしてきました。しかし、写像の説明の時に挙げたように秀吉の逸話ではひもの本数の方が多かったです。つまり、木と対応しないあまりのひもが出てくるのです。なので、この例は実際には全単射ではありません。
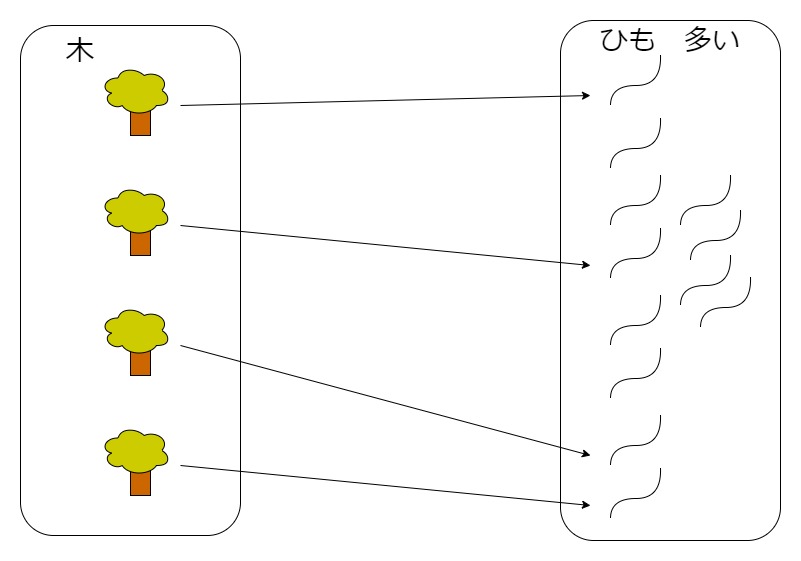
例:実際のひもときの対応
木の本数の方が実際には少なかったので、「木$\rightarrow$ひも」は一意的で写像だと言えます。逆に、「ひも$\rightarrow$木」では余ったひもが対応する木が存在しません。
以上から、秀吉の例は全単射ではなかったことになります。しかし、木の本数は実際に数えられています。計算では、「元のひも$-$から余ったひも$=$(使ったひも)」を求めていたわけです。従って、使ったひもだけ考えると全単射になっています。
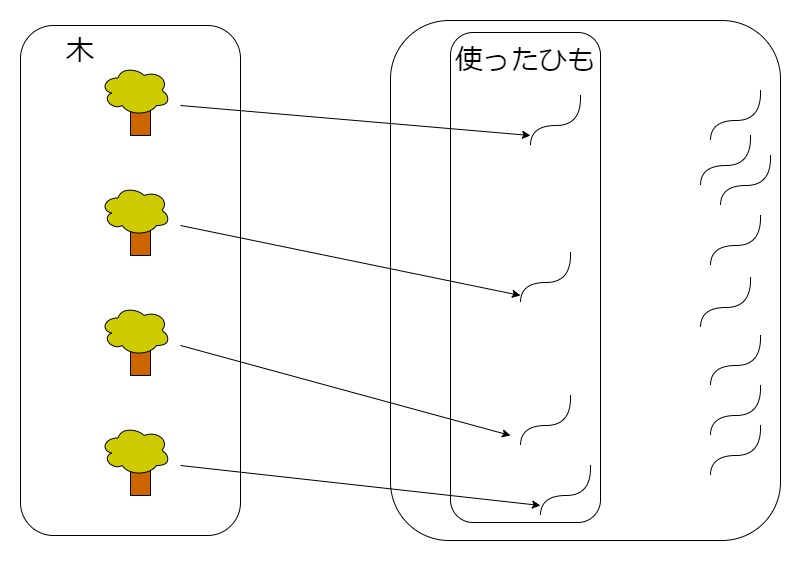
例:使ったひも全体と木全体の対応
上の図のようにひもを使ったひもだけに制限する、「ひも$\rightarrow$木」も写像となります。こうなると、「使ったひも」と「木」の間に全単射が作れますね。
さて、写像「$f:木\rightarrow ひも$」は木に対してひもは一本括り付けるので、一つのひもで異なる2本の木は括り付けられません。写像$f$について、ひも一本に対して括り付けられた木が一本であることを論理式で次のように書けます。
$$\forall x, y \in X(f(x)=f(y) \Rightarrow x=y)$$
この場合、写像は本題の一つである「単射」だと呼ばれます。
全射編
次もひもの例で考えられますが、少し題材を変えてみます。
$X$:霊長目(猿の仲間)全ての集合 $Y$:霊長目での科すべての集合
$f:X \rightarrow Y((猿) \mapsto (猿の属する科))$
動物の分類は、生物学ではよくあることですが矛盾なく分けられている必要があります。
例えば、「テナガザル」と名につく霊長目の動物は「テナガザル科」ですが、私たち人間が属する「ヒト科」ではありません。
霊長目の動物たちは、いずれかただ一つの科に属しています。ここから、写像$f$が作れますね。
そして、テナガザル科と言っても一種類だけではありません。「アジルテナガザル」や「シロテナガザル」、紛らわしいですが科の一段下の分類「テナガザル属」と言うものもあるそうです。例の写像$f$は、霊長目の動物の科を返すためこれらの像はすべて「テナガザル科」となります。
ここから、写像$f$は秀吉の例のような一対一対応ではないことがわかります。
では、例の$f$にはどんな特徴があるでしょう。それは、すべての科に対して属している動物が必ずいると言うことです。
テナガザル科となる動物は、先に挙げた3つ(他3種類)も候補があるためただ一つに決まりません。以上から、科の集合から動物への写像は作れず全単射ではありません。しかし、テナガザル科の動物が霊長目の中にいることはわかります。つまり、像集合$f(X)$の元であると言うことです。
そして、分類という目的から属さない科は存在しないので何かしら属する霊長目の動物が存在します。つまり、$f(X)=Y$となるわけです。この性質を満たす写像を「全射」と呼びます。
定義 単射・全射
それでは定義していきます。
$U$:普遍集合 $X,Y \subset U$
$f:X \rightarrow Y$:写像
$f$は単射($\rm{injective}$)$\overset{def}{\iff} \forall x, y \in X(f(x)=f(y) \Rightarrow x=y)$
$f$は全射($\rm{surjective}$)$\overset{def}{\iff} f(X)=Y$
単射の英訳「$\rm{injective}$」は日本語では「入射」です。これは、木の集合がひもの集合の一部(部分集合)として入っているように見れるによります。全単射が存在することは、同値関係でした。同値関係は、集合として形が違うが似ていることを示すものでした。なので、ひもの集合の中には木の集合と似たもの(今回は個数)を持つ部分集合があり、写像としてはその一部に入っていくように見えます。以上からこの単語なのだと考えられます。
全射の英訳「$\rm{surjective}$」は日本語では「上射」です。これは、値域の集合が定義域の集合の上に載っているように見えることによります。例でみたように、$f(X)=Y$から少なくとも$X$は$Y$の元の数以上の元を持っており、全射は明らかに定義域側の集合の方が基本大きくなります。ここから、より大きな台(定義域)の上に値域が乗っているようなイメージができます。

例:単射・全射のイメージ図
イメージは上の図を想定しています。定義域を主体とすると次のように言えます。
- 単射:値域の中へ入っていく。
- 全射:値域の台になる。
全射の絵で点線になっているのは、実際には$X$の元を$f$で写すと像集合に入るためです。そう考えると全射は、値域が上から定義域を押さえつけているとも言えます。
全単射の双射のように直訳した方が、イメージしやすい場合もあるわけです。
さて、単射と全射は全単射では成り立っていたことが少し抜けていると言えます。
- 単射〇一つの値域の元に定義域の元は一つ
- 単射×すべての値域の元と対応させられていないかもしれない。
- 全射〇すべての値域の元に対応する定義域の元が存在
- 全射×値域の元一つにたくさん対応する定義域の元があるかもしれない。
- 全単射は、すべての定義域の元と値域の元一つずつ写像で関係を持っている。
このように、単射と全射は互いに全単射になるための情報を持っており組み合わせると全単射になりそうな気がします。それが次の命題です。
$U$:普遍集合 $X,Y \subset U$ $f:X \rightarrow Y$:写像
$$fは全単射である. \iff (fは単射) \wedge (fは全射)$$
$\Rightarrow$について,
$f$は全単射より, 逆写像$f^{-1}:Y \rightarrow X$が存在する.
全射であることは, $Y=f(X)$を示せば十分である.
任意の$y \in Y$に対して$f^{-1}(y) \in X$である.
$\mathrm{id}_{Y}=f \circ f^{-1}$より, $y=(f \circ f^{-1})(y)=f(f^{-1}(y)) \in f(X)$である.
従って, $Y \subset f(X)$であり逆は像集合の定義から明らかである.
単射であることは, 任意の$x,y \in X$に対して「$f(x)=f(y) \Rightarrow x=y$」を示せば十分である.
$\mathrm{id}_{X}= f^{-1} \circ f$と$f(x)=f(y)$より次のように変形できる.
$x=(f^{-1} \circ f)(x)=f^{-1}(f(x))=f^{-1}(f(y))=(f^{-1} \circ f)(y)=y$.
以上から, $f$は単射かつ全射である.
$\Leftarrow$について,
$f$が全射より任意の$y \in Y$についてある$x \in X$で$y=f(x)$と書ける.
これによって, $g:Y \rightarrow X(y=f(x) \mapsto x)$を定義する.
well-definedは, 任意の$x, y \in Y$に対して「$x=y \Rightarrow g(x)=g(y)$」を示せば十分である.
$f$の全射性から$x,y$についてある$a,b \in X$によって$x=f(a), \; y=f(b)$と書ける.
$f(a)=x=y=f(b)$と$f$が単射であることから, $a=b$である.
よって, $g(x)=a=b=g(y)$である.
$g \circ f =\mathrm{id}_{X},f \circ g=\mathrm{id}_{Y}$について, 元で一致することを確かめれば十分である.
任意の$x \in X, y \in Y$について, $(g \circ f)(x)=g(f(x))=x = \mathrm{id}_{X}(x)$である.
$a \in X$により$y=f(a)$であるため, $(f \circ g)(y)=f(g(y))=f(a)=y=\mathrm{id}_{Y}$である.
以上から, $g$は$f$の逆写像であり$f$は全単射である.
$\square$
証明の補足として、合成写像の途中で$f(x)=f(y)$から$f^{-1}(f(x))=f^{-1}(f(y))$のような変形を行っています。これは、$f^{-1}$が写像として$\rm{well – defined}$であることを利用しています。
集合論を学んだ場合、ほとんどが全単射の定義を今回の言いかえ側(命題の右側)でしています。しかし、単射全射は全単射より解釈が難しく全単射の一対一対応があまり見えません。先に全単射を考えれば、単射と全射はそれから緩めたものだとすることで認識しやすいと思います。
考察 単射から全単射を作る
さて、全射の方は望み薄ですが単射の方では何やら全単射らしきものができていましたね。実は、単射が存在する場合は全単射を作ることができます。ちょっと合成写像を使うだけで。
$f:X \rightarrow Y$:単射な写像
- $f’:X \rightarrow f(X)(x \mapsto f(x))$は全単射である.
- 包含写像$i:f(X) \rightarrow Y(y \mapsto y)$との合成で$f$と一致する.($i \circ f’=f$)
以下は, 可換図式である.
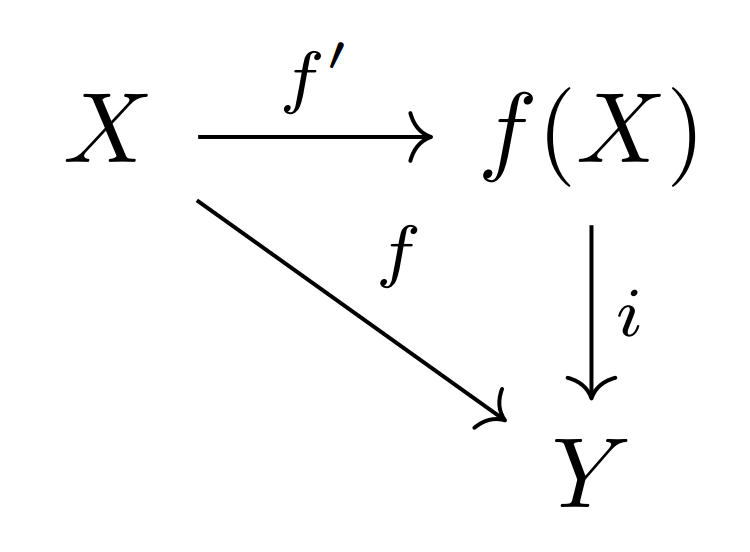
合成写像と一致するかは、簡単なのでやってみてください。
このように、$f(X)$を途中で挟むことで導入の単射の絵で値域に入っていくと言った解釈がよりしっくりくると思います。
$f’$が全単射であることは、$f(X)$が値域になったことで全射、単射であることは先の命題の証明と全く同じ手法で説明できます。
そして$X \cong f(X)$から、$X$は$Y$の部分集合とみなせます。(同型による同一視)
このとき、「$X$は$Y$に埋め込める」と言います。
単射が存在することは、自然に部分集合であることを主張していたのです。
(関連する記事:部分環の場合)
おわりに
全単射を先に取り上げたため、単射と全射を数え上げや分類と言った見方からしっくりくるようにできたと思います。実は、全射の導入をひもではなく動物の分類にしたのかは理由があり、後々の常に全射になる例の一種だからです。それは、本題「ベルンシュタインの定理」には不要なのでこの話が完結した後に登場するでしょう。また、この本題を示すための道具は全単射と単射の登場によって既にそろっていたりします。
そのための最後の準備「集合の濃度」を次回は取り扱います。(もうすぐゴールです!)
以上、ケンけんでした。
参考文献
導入の霊長目の参考にさせていただいた分類についてのサイト

