こんにちは!ケンけんです。前回は写像をよく使われる場合と直積集合での定義を見ました。
今回は、写像の演算の一つ制限写像を定義していきます。
キーワード:写像の制限(制限写像)
導入
写像の定義として直積集合を使った方法がありました。
$U$:普遍集合 $X,Y \subset U$
$f =\{(x,y) \in X \times Y| \forall x \in X, \exists ! y \in Y((x,y) \in f)\}$:$X$から$Y$への写像($mapping$)
$X$から$Y$への写像$f$は$f:X \rightarrow Y(x \mapsto y)$と表現する。
$x \in X$について$(x,y) \in f$となる$y \in Y$を$x$の像($image$)と呼ぶ。
このとき、$f(x)=y$と書く。
つまり集合の言葉で、新しく写像を作ることができると言えます。
定義域の集合$X$を、部分集合$A$($\subset X$)に置き換えて考えてみます。
単純化のために、$X$の部分集合として$x_{0} \in X$について$\{x_{0} \} \times Y$とすると$f$を使って何が説明できるでしょう。
このとき、写像$f$の元となりうる$y_{0} \in Y$はただ一つだったので、$\{x_{0} \} \times Y$の元として見ても$(x_{0}, y_{0}) \in f$だと言えます。そして、$\{(x_{0}, y_{0})\}$は写像の定義を満たします。
従って、元の写像$f$から新しい写像が構成できました。これを仮に$g=\{(x_{0}, y_{0})\}$と置きます。この対応の仕方は、$f$により定まっており次のことが成り立ちます。$$g(x_{0})=y_{0}=f(x_{0})$$ここから、$g$という新しい記号を使わず、$f$を使って表現した方がよさそうです。これが、写像の制限(または制限写像)です。
次の絵は、前回の木とひもの対応の例です。
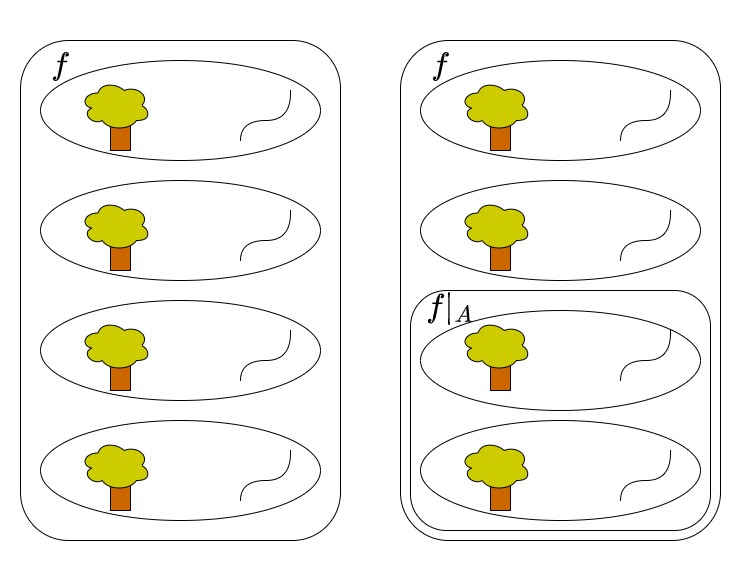
例:写像$f$と$A \subset X$による制限$f|_{A}$の図
このように、制限は元の集合$f$の一部を見ているだけです。従って$f_{A}$は、$f$を使って定義しても木($A$に含まれる木)に対して一意的にひもが決まっているため写像として$well$-$defined$です。
定義
それでは、定義します。
$U$:普遍集合 $X,Y \subset U$ $A \subset X$
$f:X \rightarrow Y$:写像
$g=\{(a,y) \in A \times Y|y=f(x) \}$:$f$の$A$への写像の制限($restriction$)
$g=f|_{A}$と書く。
$f$は$f|_{A}$の$X$への延長($prolongation$)
$g$の対応のさせ方は、導入でもふれたように次のようになります。
$$\forall a \in A(f|_{A}(a)=f(a))$$
対応する元は、$A \times Y$と$X \times Y$のどちらの元として考えても同じです。
像集合
この写像の利用先が、次回の主題となる写像の合成です。
この節ではその準備として、写像の値域について考えます。
$X=\{x_{1}, x_{2} , x_{3}\}$ $Y$:集合
$f:X \rightarrow Y$:写像
- $f \subset X \times Y$は定義から$f=\{(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})\}$ $(y_{1},y_{2},y_{3} \in Y)$
つまり、次のような$Y$の部分集合$Z$が考えられます。$$Z=\{y_{i} \in Y| \forall i \in \{1,2,3\}((x_{i} ,y_{i}) \in f)\}=\{y_{i} \in Y| \forall i \in \{1,2,3\}(y_{i}=f(x_{i}))\}$$
$X$の元に対応する$Y$の元だけを集合としたものです。この$Z$は、$X$と$f$によって定まるため$f(X)$と一目見てわかるようにします。これは、$x \in X$について対応する$y \in Y$を「$y=f(x)$」と書くことからイメージできます。
先ほどの$Z$を、一般の$X$にも考えたいです。そうすると、次のように表記されます。$$f(X)=\{y \in Y|\exists x \in X((x,y) \in f)\}=\{y \in Y| \exists x \in X(y=f(x))\}$$
先ほどの$Z$は、元を数え切れる集合だったので添え字部分の$i$に関する条件で記述しました。一般の場合は数え切れない場合があるため「対応する$x \in X$の存在」に書き換えることで対応します。
この部分集合は、今後の定義に用いられる重要なものなので特別に「像」という名前がついています。
$U$:普遍集合 $X,Y \subset U$ $A \subset X$
$f:X \rightarrow Y$:写像
$f(A)=\{y \in Y|\exists a \in A((x,y) \in f)\}$:$f$の$A$による像($image$)
代数学では、$f(X)$を$\mathrm{Im}f$と書いたりもします。
おわりに
今回は、写像の合成のための下準備として写像の制限を取り上げました。しかし、写像の制限単体の話題もあるためまた補助記事で書きたいです。
像は次回の合成のために導入しましたが、代数学で$\mathrm{Im}f$と書くように特徴的な部分集合になるため大切な対象です。集合の言葉だけでもいろいろな性質があるので、集合の$X,Y$を部分集合などに置き換えて考えると学びになると思います。
以上、ケンけんでした。

