 学習帳
学習帳 MOD-L-9:剰余と局所化をテンソル積で tensor product
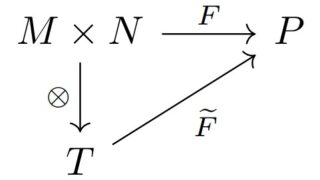
tensor product テンソル積は定義の面倒さもそうだが何に利用するのか初見ではイメージが付きにくい。今回は、利用の一つとして加群の剰余加群・局所化のテンソル積での変形により剰余体と加群のテンソル積をひとつの加群に整理できることを示す。
 学習帳
学習帳  学習帳
学習帳  学習帳
学習帳  代数基礎
代数基礎 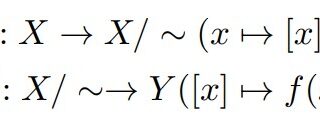 素朴集合論(NST)
素朴集合論(NST)  素朴集合論(NST)
素朴集合論(NST) 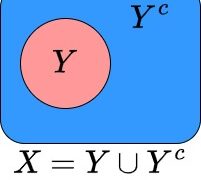 素朴集合論(NST)
素朴集合論(NST) 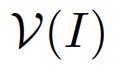 学習帳
学習帳 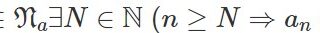 位相構造
位相構造  学習帳
学習帳