 代数基礎
代数基礎 BR1-7:部分構造だけど拡大全体が大事 部分環と拡大環
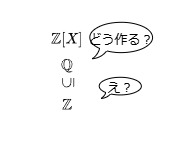
部分環と拡大環 環の特別な部分集合としてイデアルがあったが、これは環にはならない。環構造を保つ部分集合として部分環が存在し、元の環を合わせて拡大と呼ばれる。部分環側が定義だが、含む側である拡大環にも視点が行く。今回はイデアルとの差を考えるとともに単位的な環だからこそ起こる差を見ていく。
 代数基礎
代数基礎 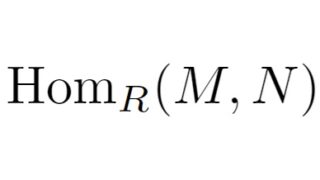 加群基礎
加群基礎 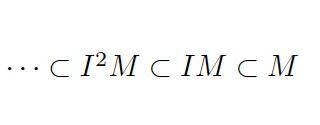 加群基礎
加群基礎 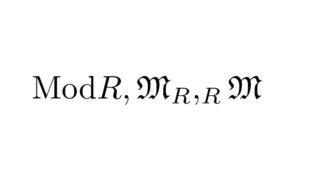 加群基礎
加群基礎 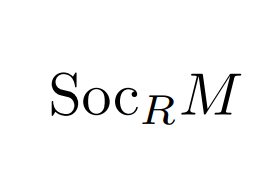 学習帳
学習帳 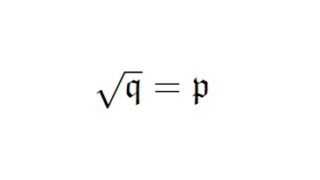 可換環論
可換環論 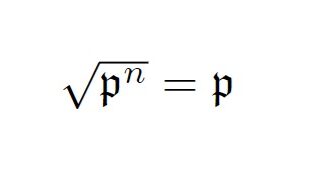 代数基礎
代数基礎  代数基礎
代数基礎 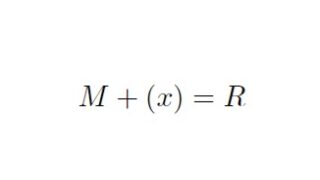 代数基礎
代数基礎  代数基礎
代数基礎