こんにちは!ケンけんです.
この記事では,加群に作用させて零にできる元として零因子を取り上げました.
今回は逆に加群の元を作用で零化する環の元に注目します.
キーワード:零化イデアル
本記事では,特に言及しない場合は以下の記号を用いる.
$R$:単位的可換環 $M$:$R$加群 $N,P \subset M$:$M$の部分加群
導入
剰余環$\mathbb{Z}/12\mathbb{Z}$は,次の作用で$\mathbb{Z}$加群になります.
$$\mu:\mathbb{Z} \times \mathbb{Z}/12\mathbb{Z} \to \mathbb{Z}/12\mathbb{Z}((r,\overline{x}) \mapsto \overline{rx}).$$
このとき,$I=(12)$の元を作用させることで$\mathbb{Z}/12\mathbb{Z}$は零化されます.
($I(\mathbb{Z}/12\mathbb{Z})=\{\sum_{i}r_{i}\overline{x_{i}}|r_{i} \in I, \overline{x_{i}} \in \mathbb{Z}/12\mathbb{Z}\}=0$を意味する)
そして$I$は$\mathbb{Z}$のイデアルとなっています.
ここから,加群を零加群にする元全体に意味があるといえます.
先ほどの$I=(12)$は,集合表示で次のように説明できます.
$$I=\{r \in \mathbb{Z}|r(\mathbb{Z}/12\mathbb{Z}) =(\overline{0})\}.$$
この$I$を$\mathrm{Ann}_{\mathbb{Z}}(\mathbb{Z}/12\mathbb{Z})$と書き,零化イデアルと呼びます.
剰余環の場合は,剰余を取っている$12$倍をすることで$0$になることがわかります.
これを一般の加群で考えると,$I=(12)$は次のようにみなせます.
$$\{r \in \mathbb{Z}|r\mathbb{Z}=(12)\}.$$
しかし,この表現ではイデアルになりません.
なぜなら,$0\mathbb{Z}=0 \neq (12)$から零元を持てないからです.
これは一般の環や加群でも同様です.
これは,条件式に等号を使っていることが問題になっています.
なので次のようにすればイデアルであり,剰余環の例を説明できます.
$(P:_{R}N)=\{r \in R|rN \subset P\}$はイデアルである.
$0N=0 \subset P$のため,$(P:_{R}N)\neq \emptyset$である.
任意の$r \in R$及び$x,y \in (P:_{R}N)$を取る.
$xN, yN \subset P$のため,
$(x+y)N \subset xN+yN \subset P$である.
従って,$x+y \in (P:_{R}N)$となる.
また$rxN \subset xN \subset P$のため,$rx \in (P:_{R}N)$である.
以上から,$(P:_{R}N)$は$R$のイデアルである.
$\square$
これにより,先ほどの$\mathbb{Z}/12\mathbb{Z}$に対する$I=(12)$は次のように表現できます.
$$I=(12)=(0:_{\mathbb{Z}}\mathbb{Z}/12\mathbb{Z})$$
この$\mathbb{Z}/12\mathbb{Z}$を部分加群$N=(\overline{2})$に置き換えることで,
$J=(6)=(0:_{\mathbb{Z}}N)$と表現できます.
定義 AnnM
それでは定義していきます.
一般の呼び方は諸説ありなので,よく利用されている方を採用します.
$M$:$R$加群 $N,P \subset M$:$M$の部分加群
$(N:_{R}P)=\{r \in R|rP \subset N\}$:$N$と$P$の$\rm{colon \; submodule}$
$\mathrm{Ann}_{R}P=(0:_{R}P)$:$P$の零化イデアル($\rm{Annihilator}$)
せっかくなので,有理整数環以外の例を見てみましょう.
$R=M=\mathbb{Z}[\sqrt{3}]$とする.
イデアル$I=(1+\sqrt{3})$に対し,$((2):_{R}I)=(2,1-\sqrt{3})$である.
$(1+\sqrt{3})(1-\sqrt{3})=-2$から,$1-\sqrt{3} \in b(2:_{R}I)$である.
また$2I \subset (2)$は明らかである.
従って$(1-\sqrt{3})I \subset (2)$から,
$(1-\sqrt{3}) \subset (2:_{R}I)$である.
逆に,任意の$a+b\sqrt{3} \in (2:_{R}I)$を取る.
このとき,ある$c+d\sqrt{3} \in R$により
$(a+b\sqrt{3})(1+\sqrt{3})=2(c+d\sqrt{3})$と書ける.
このとき次の合同式が得られる.
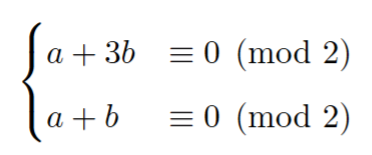
従って$a\equiv -b (\mod 2)$である.
また,$a+3b\equiv 2b\equiv 0 \pmod 2$となる.
これは$b \in \mathbb{Z}$によらず成り立つため,
条件式は$a+b \equiv 0 \pmod 2$のみである.
以上から,次の表記を得る.
$$(a+b\sqrt{3})=(a+b)-b(1-\sqrt{3}) \in (2,1-\sqrt{3}).$$
従って,$(2:_{R}I) \subset (2, 1-\sqrt{3})$となる.
$\square$
通常の加群と剰余加群の言いかえ
導入では零化をわかりやすくするために,
剰余加群を例として使いました.
これは一般の加群の$\rm{colon \; submodule}$で言いかえができます.
$(N:_{R}P)=\mathrm{Ann}_{R}((N+P)/N).$
任意の$r \in (N:_{R}P)$に対し,$rP \subset N$である.
任意の$\overline{n+p} \in (N+P)/N$に対し,
$rp \in N$のため,$r(\overline{n+p}) =\overline{0}$となる.
従って,$r \in \mathrm{Ann}_{R}((N+P)/N)$である.
逆に任意の$r \in \mathrm{Ann}_{R}((N+P)/N)$を取る.
任意の$\overline{n+p} \in (N+P)/N$に対し$r(\overline{n+p}) =\overline{0}$より,
$rn+rp=n’ \in N$と書ける.
従って$rp=n’-rn \in N$から$r \in (N:_{R}P)$である.
以上から,$(N:_{R}P)=\mathrm{Ann}_{R}((N+P)/N)$である.
$\square$
おわりに
一般的には零化イデアルの方を使用しますが,
ごくまれに$\rm{colon \; submodule}$で扱うこともあります.
そのようなときは,剰余加群に置き換えて零化イデアルで考えることになります.
また今後きれいな加群を扱う際には必要になってくるため,記事にしました.
以上,ケンけんでした.

