こんにちは!ケンけんです.
今回は,直積集合に環構造を導入し環論における直積構造の意味を考えていきます.
キーワード:環の直積
この記事では,環はすべて単位的可換環とします.
$R,T,R_{i}(i \in I)$:環
$I \subset R$:イデアル
導入と定義 環の直積
ベクトルでは,成分ごとに加法とスカラー倍を定義していました.
これは,ベクトル全体の集合が環上の加群(体上の加群)となることを意味しています.
そして,成分の元は体や環の元であり加群の直積とみなせる.
同様に,「成分ごとの乗法」で直積集合に環構造を持たせることができます.
$T=\prod_{i \in I}R_{i}$
$T$は次の演算により,環となる.
$+:T\times T \to T(((x_{i}),(y_{i}))\mapsto (x_{i}+y_{i}))$
$\bullet : T \times T \to T(((x_{i}),(y_{i}))\mapsto (x_{i}y_{i}))$
零元は$0_{T}=(0_{R_{i}})$,単位元は$1_{T}=(1_{R_{i}})$である.
$T$を環の直積と呼ぶ.
演算と零元・単位元の一意性は,成分ごとの確認で証明できます.
環で直積を考える理由として,
環の比較ツールとしてや,加群と同じ普遍性を持ちます.
次節から,それぞれ見ていきます.
比較対象として
1.整域ではない点
第一に,環の直積は必ず整域ではありません.
簡単な有理整数環で見てみましょう.
$\mathbb{Z}$は整域だが,$\mathbb{Z} \times \mathbb{Z}$は整域ではない.
- $(1,0)(0,1)=(0,0)$より,$(1,0)$は零因子となる.
- $Z(\mathbb{Z}\times \mathbb{Z}) \neq \{(0,0)\}$となり整域ではない.
これは整数に限った話ではなく,任意の環でも成り立つ.
$T=\prod_{i}R_{i}$を環の直積は,整域ではない.
$i,j,k \in I$に対し,$\delta_{ij}$を次のように定義する.
$\delta_{ij}=\begin{cases} 1_{R_{i}} & \text{($i = j$)}\\ 0_{R_{i}} & \text{($i\neq j$)} \end{cases}$
$(\delta_{ij})_{i \in I},(\delta_{ik})_{i \in I} \in T$を取る.
$j\neq k$を仮定する.
このとき,$(\delta_{ij})(\delta_{ik})=(\delta_{ij}\delta_{ik})=(0_{R_{i}})$となる.
$(\delta_{ij})\neq (0_{R_{i}})$のため,非自明な零因子となる.
従って,$T$は整域ではない.
$\square$
これは,成分の環が整域(さらには体)であっても成り立つため,
整域ではない条件を試す方法として体$k$の直積$k\times k$を考えることが多いです.
また,剰余環$R/I$が環の直積と同型ならば$I \notin \mathrm{Spec}R$となります.
直接調べずに,別の性質から素イデアルか判定する材料にできます.
2.環を分解する点
さらには,環そのものを分解する手法に利用します.
$\rm{Artin}$環と呼ばれる特殊な環の中で”小さい”環のクラスがあります.
その性質の例として,$\rm{Artin}$環は素イデアルと極大イデアルが一致かつ有限個です.
なのでこの環は半局所環ですが,
極大イデアルのべきを用いた剰余環で,
$\rm{Artin}$局所環の有限直積で表示できます.
これは同型に依存しない形なので,環の構造を直積で表現できることになります.
このように,環の直積は共通部分とは別の分解表示を与えてくれます.
普遍性は…
1.直和の必要性
加群の直積には,さらに「直和」が存在しました.
そして,直積と直和には次のような不変性が存在しました.
$\{M_{\lambda}\}_{\lambda \in \Lambda}$を$R$加群の族とする.
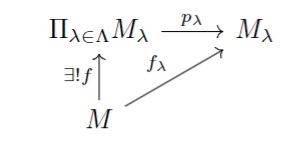
(1)任意の$R$加群$M$と各$\lambda$に対し, $f_{\lambda}:M \to M_{\lambda}$を取る.
このとき, 各$\lambda$で$p_{\lambda}f=f_{\lambda}$を満たす$f \in \mathrm{Hom}_{R}(M,\Pi_{\lambda \in \Lambda}M_{\lambda})$がただ一つ存在する.
つまり, 以下の図式を可換にする$f$がただ一つ存在する.($p_{\lambda}$は$\lambda$成分の射影)
(2)任意の$R$加群$M$と各$\lambda$に対し, $g_{\lambda}:M_{\lambda} \to M$を取る.
このとき, 各$\lambda$で$g_{\lambda}=gi_{\lambda}$を満たす$g \in \mathrm{Hom}_{R}(\bigoplus_{\lambda \in \Lambda}M_{\lambda},M)$がただ一つ存在する.
つまり, 以下の図式を可換にする$g$がただ一つ存在する.($i_{\lambda}$は包含写像)
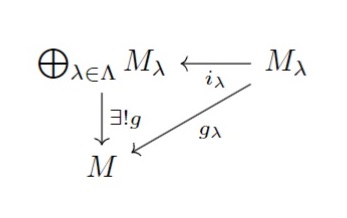
そして,これが環でも成立する場合,
写像が線形写像ではなく環準同型に置き換えられることです.
しかし,直和側の包含写像は環準同型になりえません.
包含写像$i:R \to R \times T(x \mapsto (x,t))(t \in T)$を取る.
1.加法が成り立つためには$t=0_{T}$である.
- $x,y \in R$に対し,$i(x+y)=i(x)+i(y)$を仮定する.
- $(x+y,t)=(x,t)+(y,t)$より,$(0,t)=0_{R\times T}$となる.
- よって$t=0_{T}$となる.
2.単位元から単位元へ写らない
- $i(1_{R})=(1_{R},0_{T})\neq 1_{R\times T}$である.
- よって$i$は環準同型ではない.
加群のように環から,直和を定義することは可能です.
しかし,普遍性を持たない対象という意味でそれほど価値がないためか,
環論の書籍では直積のみで「環の直和」は定義されていません.
2.直積の不変性
しかし射影は環準同型写像のため,直積の不変性は成り立ちます.
$p_{i}:\prod_{i}R_{i} \to R_{i}$を$R_{i}$への射影とする.
任意の$i \in I$に対し $f_{i}:T \to R_{i}$を取る.
このとき, 各$i$で$p_{i}f=f_{i}$を満たす$f \in \mathrm{Hom}_{R}(M, \prod_{i \in I}R_{i})$がただ一つ存在する.
つまり, 以下の図式を可換にする$f$がただ一つ存在する.
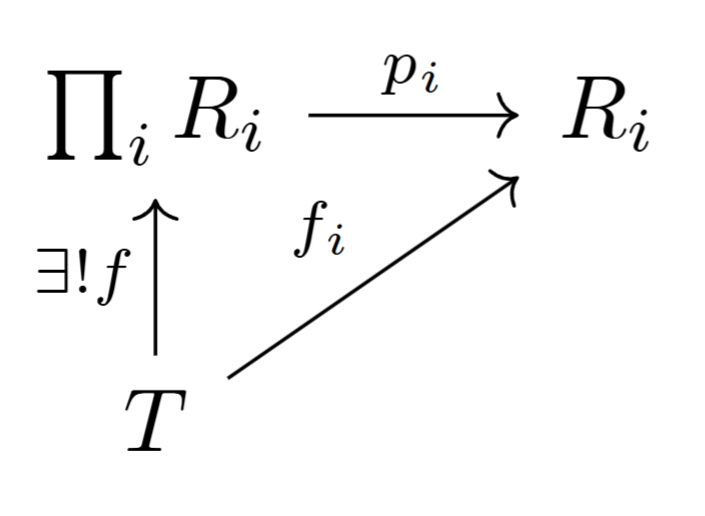
$f:T \to \prod_{i}R_{i}(t \mapsto (f_{i}(t)))$を定義する.
$\rm{well}$-$\rm{defined}$性と加法性,一意性は,
命題 MOD1-8-3(1)と同様の手法で証明できる.
従って,乗法及び単位元に関する性質を示せば十分である.
$t,u \in T$に対し,
$f(tu)=(f_{i}(tu))=(f_{i}(t)f_{i}(u))=(f_{i}(t))(f_{i}(u))=f(t)f(u)$.
また,$f(1_{T})=(f_{i}(1_{T}))=(1_{R_{i}})=1_{\prod_{i}R_{i}}$である.
以上から,$f$は環準同型となる.
$\square$
以上から,環の直積は普遍性を満たします.
そして加群と同様に圏論的直積として意味を持つわけです.
おわりに
環の直積は,多くの書籍で定義のみされてあとは諸性質を当然のように利用してきます.
普遍性は圏論まで進まないと,イメージはしませんが非整域であることは知っていると,
検証に有用なので共有しました.(考えれば当たり前なんですが…)
以上,ケンけんでした.