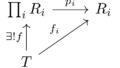こんにちは!ケンけんです.
このBR2では,可換環の重要な具体例である多項式環を扱います.
今回はその導入記事となります.
この記事では,環はすべて単位的可換環とします.
$R$:環
$\mathbb{Z}$:有理整数環
$\mathbb{Z}[X]$:整数係数の多項式全体の集合
式といえば方程式? 多項式
高校数学で式といえば「方程式」がすぐに思い浮かぶのではないでしょうか.
実際に,式変形に始まり関数の値を求めるためにも「方程式を解く」ことは出てきます.
形式は「数式$=0$」の表記が該当します.
例えば次のような例があります.
- 図形の表現として方程式(高校数学 数学Ⅱ)
- 微分法における極大極小点導出
- 関数方程式(数学Ⅲまたは微分方程式)
- 線形代数全般(行列は連立方程式,行列式はその解の分母)
どれも同じ「方程式を解く」操作で得られる結果に注目しています.
一方多項式は,複数の項を持つ整式(数と文字$x,y,z$など)でした.
[整式とは,数と文字($x,y,z$など)を整理した分母$1$の式の総称]
一つの項の整式は,単項式とも呼んでいました.
しかし,登場する中学数学以降は式変形に重きを置くためほぼ意識しません.
実際に,整式と多項式はほぼ同じ扱いをされます.
すべての整式の集まりとして 多項式環
式の中で,多項式の環を取り挙げる理由は様々です.
1.代数的根拠
まずは,構造上重要である「演算で閉じる」ことです.
例えば,単項式の和は多項式となりえるため加法で閉じません.
(例:$2x,3y$は単項式だが$2x+3y$は整理できないので多項式)
方程式の中には「代数方程式」と呼ばれる,有理数係数の「多項式=0」が存在する.
多項式$=0$となるとき,文字の組を「多項式の根」と呼びます.
例えば,方程式「$2x+3y=0$」は多項式$F=2X+3Y$の根は$(x,y)$だといえます.
この一般化として,環の元(整数環$\mathbb{Z}$など)を係数とする多項式も考えられます.
(コンピュータへの利用として,入力処理が整数値・整数係数多項式が多いことも挙げられます.)
2.代入に関する拡大
次に,拡大環に関する視点です.
以前の記事で拡大環を構成することは,難しいことを挙げました.
この構成として最も簡単な方法が,代入操作でこれは環準同型写像となります.
$\mathbb{Z}[X]$の不定元$X$に虚数単位$i$を代入した$\mathbb{Z}[i]$は,$\mathbb{Z}$の拡大環でした.
($\mathbb{Z}[i]$は$\mathbb{Z}$上$1,i$で”生成”された環と説明できる)
このように,係数に置いた環の拡大環を容易に作成できます.
また代入は全射であるため,$\mathbb{Z}[i]$は$\mathbb{Z}[X]$の性質をいくつか引き継ぎます.
3.幾何学とのつながり
環論の利用としては,数学的な意味があるのは幾何学への応用です.
例えば円の方程式「$x^{2}+y^{2}=1$(半径$1$の円)」のグラフを次の集合とみなせます.
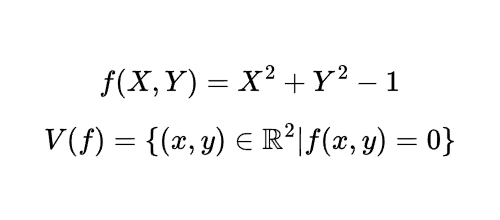
このグラフは,$\mathbb{R}$の閉代数的集合($\rm{closed \; algebraic \; subset}$)と呼ばれるものです.
特に,別分野の代数多様体(代数幾何学)の簡単な例になります.
可換環論は当初代数幾何学と二人三脚で発展してきたので,
「幾何学$\iff$多項式環」の関係の深さは納得できるものです.
記事群の展望
さて,ここまで動機付けを行ってきましたが具体的に,何を扱うかを示していきます.
1.多項式と多項式環の概要と厳密な定義を並走して定義する
多項式環は使えないと意味がないため,まず前提として環上での基本的な情報を取り挙げます.
そしてこの段階で,厳密な定義である「次数付き環」による定義を与えます.
この定義によって,わからない情報として用いた文字が定義できます.
実はこの定義部分は学習長で既に書いていたりしますが,
こちらではより詳しく取り上げる予定です.
2.応用:代数と有限生成を取り挙げる
応用として環準同型写像を利用した「代数」という概念も取り扱います.
具体的には環準同型写像$f:R\to T$に対し,
作用$\mathrm{Im}f\times T \to T$を$T$の乗法で定義し,
$R$加群とみなして$T$を$R\text{-}$代数と呼びます.
これは,代入操作の一般化として導入します.
おわりに
導入記事なので,内容浅目に抑えました.
以前の学習帳の記事と重複してしまう部分もありますが,
うまく差別化できるよう書いていく予定です.
以上,ケンけんでした.