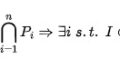こんにちは!ケンけんです.
今回は,極大イデアル全体の共通部分「Jacobson根基」を取り扱います.
キーワード:Jacobson根基
この記事では,環はすべて単位的可換環とします.
$R$:環
$\mathrm{Spec}R$:環$R$の素イデアル全体の集合
$\mathrm{Max}R$:$R$の極大イデアル全体の集合
$\mathcal{V}(I)$:イデアル$I$を含む素イデアル全体の集合($\rm{Zariski}$閉集合)
$N(R)$:$R$のべき零根基
$1$で$1_{R}$を表す.
導入と定義 Jacobson根基
根基イデアルが登場した際に,素イデアル全体の共通部分として$N(R)$がありました.
今回のJacobson根基の定義は,ここで取る素イデアルを極大イデアルに置き換えたものです.
$J(R)=\bigcap_{\mathfrak{m} \in \mathrm{Max}R}\mathfrak{m}$:$R$のJacobson根基
構成と極大イデアルの性質から,任意の環$R$に対して$N(R) \subset J(R)$が常に成り立ちます.
また構成から任意の極大イデアル$\mathfrak{m}$に対し,$J(R) \subset \mathfrak{m}$です.
従って,$J(R)$の元$x$は任意の剰余体$R/\mathfrak{m}(\mathfrak{m} \in \mathrm{Max}R)$上で$0$となります.
極大イデアルは,属さない元とのイデアルの和で環全体にすることができました.
この性質と似た事実により,$J(R)$の元を特徴づけることができます.
$x \in R$に対し,以下互いに同値である.
(1)$x \in J(R)$,
(2)任意の$y \in R$に対し,$1-xy \in R^{\times}$である,
(3)イデアル$I$に対し,$I+(x)=R$ならば$I=R$である.
特に,イデアル$I$に対し$I+J(R)=R$ならば$I=R$となる.
(1)$\Rightarrow$(2)
ある$y \in R$で$1-xy \notin R^{\times}$を仮定する.
非単元$1-xy$はある$\mathfrak{m} \in \mathrm{Max}R$の元となる.
しかし$xy \in \mathfrak{m}$のため,$1 \in \mathfrak{m}$となり矛盾する.
従って任意の$y \in R$で$1-xy \in R^{\times}$となる.
(2)$\Rightarrow$(3)
イデアル$I$に対し$I+(x)=R$を仮定する.
このとき,ある$a \in I,r \in R$により$a+rx=1$と書ける.
(2)から,$a=1-xy \in R^{\times}$のため$I=R$である.
(3)$\Rightarrow$(1)
$x \notin J(R)$を仮定すると,ある$\mathfrak{m} \in \mathrm{Max}R$で$x \notin \mathfrak{m}$となる.
従って$\mathfrak{m}+(x)=R$となる.(参考)
(3)から$\mathfrak{m}=R$のため,極大イデアルの定義に矛盾する.
従って,$x \in J(R)$となる.
$\square$
イデアル$I$に対し,$I+J(R)=R$を仮定する.
このとき,ある$x \in J(R)とa \in I$で$a+x=1$と書ける.
よって$I+(x)=R$のため,(1)$\iff$(3)から$I=R$となる.
$\square$
有限の共通部分であることの利用
設定としてこの節では,環$R$に対して$\mathrm{Max}R=\{\mathfrak{m}_{1},\ldots, \mathfrak{m}_{n}\}$とします.
素イデアル避けの記事にて,イデアルの共通部分と素イデアルの包含に関する主張がありました.
これにより,$\mathcal{V}(J(R))$を特徴づけることができます.
(1)$\mathcal{V}(J(R))=\mathrm{Max}R$,
(2)$J(R)=\mathfrak{m}_{1}\cdots \mathfrak{m}_{n}$,
(3)$J(R)=0\Rightarrow \mathrm{Max}R=\mathrm{Spec}R$,
- 特に$N(R)=J(R)$となる.
(1)$\mathrm{Max}R \subset \mathcal{V}(J(R))$は明らかなので,逆の包含を示す.
$P \in \mathcal{V}(J(R))$に対し,$J(R)=\bigcap_{i=1}^{n}\mathfrak{m}_{i} \subset P$となる.
BR1-12-1(1)から,ある$i$で$\mathfrak{m}_{i} \subset P$となる.
$\mathfrak{m}_{i}$の極大性から,$P=\mathfrak{m}_{i}$となる.
従って,$\mathcal{V}(J(R))=\mathrm{Max}R$となる.
(2)$i\neq j$に対し,$\mathfrak{m}_{i}\neq \mathfrak{m}_{j}$である.
BR-1-5-4から,$\mathfrak{m}_{i},\mathfrak{m}_{j}$は互いに素となる.
従ってBR1-11-3(3)から,$J(R)=\bigcap_{i=1}^{n}\mathfrak{m}_{i}=\mathfrak{m}_{1}\cdots \mathfrak{m}_{n}$となる.
(3)$J(R)=0$ならば,$\mathcal{V}(J(R))=\mathrm{Spec}R$となることから従う.
$\square$
有限性を課すと,BR1-12-1(1)に従う形で$\mathrm{Spec}R,\mathrm{Max}R$のさまざまな情報が得られます.
実際に,$\mathrm{Max}R$が有限集合になる環の例をいくつか作ってみます.
$R=\mathbb{Z}/12\mathbb{Z}$:極大イデアルは$(\overline{2}),(\overline{3})$の2個
$\Rightarrow J(R)=(\overline{0})$となる.
$\Rightarrow \mathrm{Spec}R=\mathrm{Max}R$(BR1-13-3(3)より)
嫌な元の集まり? 単純化の道具として
Jacobson根基は,べき零根基の素イデアルを極大イデアルにしただけですが,
いくつかの理由から重要になります.
1.極大イデアルは有限個にしやすい
$\mathrm{Max}R$が有限集合となる状況は,自然な例や構成する方法があります.
すでに記事にしたものですと,剰余環によるイデアルの一対一対応です.
イデアル$I$を含む極大イデアルが有限個ならば,$\mathrm{Max}R/I$も有限集合となります.
他に最も簡単に有限個(実際には一つ)にする方法が,局所化です.
これは算数で長さの比から分数を導入することと同じ手法で,環の分数を定義する技術です.
専門的内容なので詳しくは言及しませんが,「素イデアル$P$で局所化」により,
$P$に対応するイデアルをただ一つの極大イデアルとする環が作れます.
以上のように,前節の情報を利用できる状況が作りやすい点が挙げられます.
2.$\mathrm{Spec}R$を単純化しやすい
これは前節で挙げた$\mathcal{V}(J(R))=\mathrm{Max}R$にできることにあります.
$R/J(R)$では$\mathrm{Spec}R=\mathrm{Max}R$となります.
導入順序は「素イデアル$\Rightarrow$極大イデアル」でしたが,
見方を変えれば「素イデアル=集合論で説明できる極大イデアルに似たイデアル」といえます.
$\mathrm{Max}R$を有限集合として剰余をとることで,
任意の素イデアルの増大列が零イデアルと極大イデアルのみにできます.

このように,$R/J(R)$上では任意の素イデアルの増大列が$0$と極大イデアルのみになります.
素イデアルの増大列の長さ($\subset$が入った回数)の最大値を環のKrull次元と呼び,
$R/J(R)$ではKrull次元が$0$であると呼びます.
極大イデアルが有限個な環では,人為的に次元$0$の環を作れる点で有用です.
他にもっと根本的な情報がありますが,現在の知識だけでも剰余で単純化されることから,
$J(R)$は「扱いずらい元を排除してくれる」と考えられるでしょう.
おわりに
極大イデアルが有限個の環で,特に一つしか持たない状況は非常に有用な環となります.
この場合$J(R)$が極大イデアルとなり,この概念が不要になってしまいます.
なので,利用されるのは極大イデアルが有限個となる環となります.
性質は,環の基本的な性質を利用するので良い演習にもなると思います.
以上,ケンけんでした.