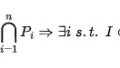こんにちは!ケンけんです.
代数学では,生成された~(例1,2)といったものがあります.
この構成自体は集合レベルの話で,他にないか気になっていました.
そこで調べてみると,位相空間論の閉包が例になっていることがわかりました.
また内部との関係も出てきたので,位相空間の理解を深めるために今回まとめていきますよ.
それでは行ってみよう!
キーワード:閉包・内部・生成された空間
注意
この記事では,開近傍の主張を利用します.(例:$\mathcal{O}_{x}(X)$は元$x \in X$の開近傍系)
閉包と内部
まずは,位相の記事から内点と触点を復習します.
$(X,\mathcal{O}(X))$:位相空間 $A \subset X$ $x \in X$
$x$は$A$の内点 $\overset{def}{\iff} \exists V \in \mathfrak{N}_{x} \; s.t. \; V \subset A$
$A^{\circ}=\{x \in X|x:Aの内点\}$を$A$の内部と呼ぶ.
($\mathrm{Int}_{X}A$とも書く.)
$x$は$A$の触点 $\overset{def}{\iff} \forall V \in \mathfrak{N}_{x} \; s.t. \; V \cap A \neq \emptyset$
$\overline{A}=\{x \in X|x:Aの触点\}$を$A$の閉包と呼ぶ.
($\mathrm{Cl}_{X}(A)$とも書く.)
今回は内部と閉包を何度も重ねることがあるので$\mathrm{Int}_{X},\mathrm{Cl}_{X}$を用います.
この2つの部分集合を生成する集合で説明できるようにすることが目標です.
閉包の表示
代数学における「生成する~」では,特定の条件を満たす部分集合の共通部分でした.
閉包の場合は,特別な閉集合による共通部分になります.
まず触点を閉集合を使った表現にしたいです.
$(X,\mathcal{O}(X))$を位相空間とし,$A \subset X$及び$x \in X$を取る.
このとき以下は互いに同値である.
(1)$x$は$A$の触点である.
(2)$\mathcal{V}=\{V \in \mathcal{A}(X)|A \subset V\}$に対し,$x \in \bigcap_{V \in \mathcal{V}}V$である.
証明は対偶を取って,開集合の世界で示します.
$W=\bigcap_{V \in \mathcal{V}}V$とおき,対偶
$x$は$A$の触点ではない$\iff$ある$U \in \mathcal{V}$に対し$x \notin U$
を示す.
$x$が$A$の触点でないと仮定すると,
ある開近傍$V \in \mathfrak{O}_{x}$に対し$V \cap A=\emptyset$となる.
よって$A \subset V^{c}$かつ$x \notin V^{c}$である.
$V^{c} \in \mathcal{V}$より,$V^{c}$が求める閉集合である.
逆に,ある$U \in \mathcal{V}$に対し$x \notin U$を仮定する.
$A \subset U$から$U \cap A=\emptyset$である.
また$x \in U^{c} \in \mathcal{O}_{x}$のため,$x$は$A$の触点ではない.
$\square$
これによって食添を閉集合で説明できるようになりました.
この補題から,$\mathrm{Cl}_{X}(A)=\bigcap_{V \in \mathcal{V}}V$となります.
そしてこの$\mathcal{V}$は,他の生成する集合と同じ構造をしていますね.
そして共通部分表示であることから次の閉包に関する同値命題が得られます.
$(X,\mathcal{O}(X))$を位相空間を取る.
このとき部分集合$A,Y \subset X$に対して,以下は互いに同値である.
(1)$Y=\mathrm{Cl}_{X}(A)$である.
(2)$\mathcal{V}=\{V \in \mathcal{A}(X)|A \subset V\}$に対し,$Y= \bigcap_{V \in \mathcal{V}}V$である.
(3)$Y$は包含関係において$A$を含む最小の閉集合である.
「$(1)\iff (2)$」は補題1そのもので,「$(2) \iff (3)$」は閉集合が任意個の共通部分で保つためすぐにわかります.
「$(2)\iff (3)$」による定義が,代数学における「生成された~」の定義部分でした.
(閉包$\mathrm{Cl}_{X}{A}$は$A$で生成された閉集合と呼んでもいい.)
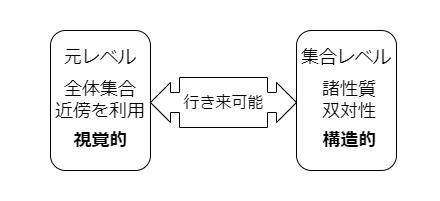
なので閉包は,触点(元レベル)と閉集合(集合レベル)の2通り定義の仕方ができます.
特に,この特徴づけを知っていればいくつかの性質が明らかになります.
$(X,\mathcal{O}(X))$を位相空間を取り,その部分集合$A,B,C_{\lambda}(\lambda \in \Lambda)$を取る.
(1)$\mathrm{Cl}_{X}(\mathrm{Cl}_{X}(A))=\mathrm{Cl}_{X}(A).$
(2)$\mathrm{Cl}_{X}(A \cup B)=\mathrm{Cl}_{X}(A) \cup \mathrm{Cl}_{X}(A)$.
(3)$\mathrm{Cl}_{X}(\bigcap_{\lambda \in \Lambda}C_{\lambda})=\bigcap_{\lambda \in \Lambda}\mathrm{Cl}_{X}(C_{\lambda})$
内部の特徴づけ
閉包が生成された閉集合だと分かったので,今度は内部の特徴づけをしてみましょう.
まず内点を触点の言葉で説明できるようにします.
$(X,\mathcal{O}(X))$を位相空間を取る.
部分集合$A$に対し,以下は互いに同値である.
(1)$x$は$A$の触点ではない.
(2)$x$は$A^{c}$の内点である.
$A$と$A^{c}$を置き換えても成り立つ.
補題1から,
$\begin{align}x \notin \mathrm{Cl}_{X}(A) &\iff \exists U \in \mathcal{O}_{x}(X) \; s.t. \; U\cap A=\emptyset\\ &\iff \exists U \in \mathcal{O}_{x}(X) \; s.t. \; U\subset A^{c}\\ &\iff x \in \mathrm{Int}_{X}(A^{c}).\end{align}$
触点の方で補題1があるので主張のようにしました.
この事実から,実は内部は「補集合の閉包の補集合」になります.
$(X,\mathcal{O}(X))$を位相空間を取り,部分集合$A$を取る.
(1)$\mathrm{Int}_{X}A=(\mathrm{Cl}_{X}(A^{c}))^{c}$.
(2)$\mathrm{Cl}_{X}A=(\mathrm{Int}_{X}(A^{c}))^{c}$.
$(1)$のみ確認する.
補題4から,$A$の内点は$A^{c}$の触点ではない.
従って,$A$の内点$x$に対し$x \in (\mathrm{Cl}_{X}(A^{c}))^{c}$である.
逆も補題4から成り立つため,$\mathrm{Int}_{X}A=(\mathrm{Cl}_{X}(A^{c}))^{c}$となる.
$\square$
そしてこの表記から内部は次の特徴ができます.
$(X,\mathcal{O}(X))$を位相空間を取る.
部分集合$A,Y$に対し,以下は互いに同値である.
(1)$Y=\mathrm{Int}_{X}(A)$である.
(2)$\mathcal{W}=\{U \in \mathcal{O}(X)|U \subset A\}$に対し,$Y=\bigcup_{U \in \mathcal{W}}U$である.
(3)$Y$は包含関係において,$A$に含まれる最大の開集合である.
また,この表示から「$A$は開集合$\iff \mathrm{Int}_{X}(A)=A$」が成り立つ.
$(2)\iff (3)$は命題2の「$(2)\iff (3)$」の対偶である.
よって$(1)\iff (2)$を示せば十分である.
まず,$\mathcal{V}=\{V \in \mathcal{A}(X)|A \subset V\}$と$\mathcal{W}$が補集合を取る操作で一対一対応する.
実際に,$U \in \mathcal{W}$に対し,$A \subset U^{c} \in \mathcal{A}(X)$であり,
$U \cup U^{c}=X,U \cap U^{c}=\emptyset$より写像$U \mapsto U^{c}$は$\rm{well}\text{-}\rm{defined}$である.
逆も同様に成り立つため命題2と系4から,
$\mathrm{Int}_{X}(A)=(\bigcap_{A \subset V \in \mathcal{A}(X)}V)^{c}=\bigcup_{U \in \mathcal{W}}U$が得られる.
$\square$
以上から,内部は含む開集合で最大のものであることがわかりました.
また,先ほど挙げた閉包の特徴付けをちょうど補集合を取ったものになっています.
よって閉包と内部は,補集合を通して移り合う「双対性」を持つことがわかります.
なので命題3の補集合を取った形で,次の性質も得られます.
$(X,\mathcal{O}(X))$を位相空間を取り,その部分集合$A,B,C_{\lambda}(\lambda \in \Lambda)$を取る.
(1)$\mathrm{Int}_{X}(\mathrm{Int}_{X}(A))=\mathrm{Int}_{X}(A).$
(2)$\mathrm{Int}_{X}(A \cap B)=\mathrm{Int}_{X}(A) \cap \mathrm{Int}_{X}(A)$.
(3)$\mathrm{Int}_{X}(\bigcup_{\lambda \in \Lambda}C_{\lambda})=\bigcup_{\lambda \in \Lambda}\mathrm{Int}_{X}(C_{\lambda})$
閉包と内部 議論の順序
生成される空間により,閉包と内部の表記が得られました.
ここからは,少し概念導入の順序について少し考えてみます.
有名どころや和書では,先に触点と内点を定義しています.(参考[1],[2])
逆に,閉包と内部を先ほどの双対的な情報として定義している本もあります.(参考[3],[4])
しかし,代数学では後者の構造で「生成する~」を定義するため,論理には問題ないはずです.
ここで考えられるのは,代数と幾何の扱う対象の差なのかと思われます.
代数は,計算規則や集合の性質に重きを置いている場合が多いです.
例えば環では,演算やイデアル,次元など集合レベルの議論が多いです.
(生成の中心となる集合が有限集合ならば,各元ごとに意味を持ちますが)
対して幾何も集合の性質を調べますが,さらにその元ごとの特徴を考えたりします.
位相空間では,点を中心とした近傍系や触点・内点等がそうです.
実際に,各点ごとに近さの動機づけを与えていました.
また今回の命題3,6は触点と内点の定義で示せますが,背理法をうまく使う場面があります.
共通部分による表現を用いた場合,直接証明になります.
よって,今回の命題3,6により閉包と内部を定義した方が構造や性質を理解しやすいといえます.
そして今回の証明から,どちらが先でももう一方の情報に復元可能です.
おわりに
ひとつ前の開近傍の記事に始まり,いくつか疑問が晴れてよかったです.
逆に閉包に対する内部のように代数学での「生成する~」の双対は何だろうと気になりますね.
以上,ケンけんでした.
参考文献
触点・内点から閉包と内部の本
[1]鎌田正良,”集合と位相”,近代科学社
[2]Nicolas Bourbaki,”General Topology,Chapter1-4″,Springer
閉包と内部から触点・内点な本
[3]Stephen Willard,”General Topology“,Dover Publications
[4]Tej Bahadur Singh,”Introduction to Topology“,Springer