こんにちは!ケンけんです。
加群の情報を引き出すとき、もっとも単純な手法と言えば集合の元レベルで確認することです。
しかし現実的にはこれが難しい、または性質を決定できないケースが多いです。
その問題を解決してくれる手法が、加群を集合レベルの比較ではなく線形写像も含めた図式の部品として検証することです。(ある種圏論の考えが出始めています)
今回はその前座かつ基本的な道具である「完全列」を取り扱います。
キーワード:完全列
前提知識:加群の線形写像について(参考)
この記事では、環はすべて単位的可換環とし加群をその上の加群とします。
導入 完全列
主の動機づけは、すべて図式で見えるようにすることです。
1.単射・全射・全単射
まずは、簡単な例たちから図式化してみます。
全射・単射・全単射は、線形写像では$\mathrm{Ker},\mathrm{Im}$により説明できました。
これをスタートにして次の主張を考えます。
$M,N$を$R$加群とし, $f \in \mathrm{Hom}_{R}(M,N)$を取る.
$0_{1}:0\to M(0 \mapsto 0_{M}),0_{2}:N \to 0(n \mapsto 0)$とする.
(1)$f$は全射$\iff \mathrm{Im}f=N=\mathrm{Ker}0_{2}$,
(2)$f$は単射$\iff \mathrm{Ker}f=\{0_{M}\}=\mathrm{Im}0_{1}$,
$\mathrm{Im}f$と$\mathrm{Ker}f$による言いかえはすでに示しています。
そして零元の対応をさせる$0_{1},0_{2}$が$R$線形写像であることもすぐわかります。
つまり全射と単射はいつでも取れる$0_{1},0_{2}$により$\mathrm{Im},\mathrm{Ker}$の一致で説明できます。
全射$f:M\to N$で考えると次の図式は$\mathrm{Im}$と$\mathrm{Ker}$が一致する図式です。
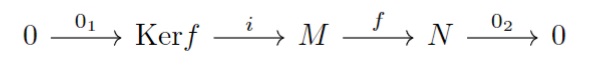
- $0_{1}:0 \to \mathrm{Ker}f(0 \mapsto 0_{M}),0_{2}:N \to 0(n\mapsto 0)$,$i$は包含写像.
- $i$は全射$\iff \mathrm{Im}f=\mathrm{ker}0_{2}$,
- $\mathrm{Ker}f=\mathrm{Im}i$,
- $\mathrm{Ker}i=\{0_{M}\}=\mathrm{Im}0_{1}$.
単射の場合は、次の図式も$\mathrm{Im}$と$\mathrm{Ker}$を保つ図式です。
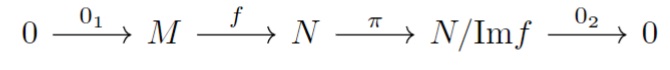
- $0_{1}:0 \to M(0 \mapsto 0_{M}),0_{2}:N/ \mathrm{Im}f \to 0(\overline{n} \mapsto 0)$,$\pi$は自然な準同型.
- $i$は単射$\iff \mathrm{Ker}f=\{0_{M}\}=\mathrm{Im}0_{1}$,
- $\mathrm{Ker}\pi=\mathrm{Im}f$,(自然な準同型の性質)
- $\mathrm{Ker}0_{2}=N/ \mathrm{Im}f =\mathrm{ker}0_{2}$.
これら2つの図式は「短完全列」と呼ぶ特別な図式です。
特に、$f$が全単射にすると, 上$2$の図式で$\mathrm{Ker}f=0,N / \mathrm{Im}f=0$から同じ次の図式ができます。

- $0_{1}:0 \to M(0 \mapsto 0_{M}),0_{2}:N \to 0(n \mapsto 0)$,
- $f$は単射$\iff \mathrm{Ker}f=\{0_{M}\}=\mathrm{Im}0_{1}$,
- $f$は全射$\iff \mathrm{Im}f=N=\mathrm{Ker}0_{2}$.
ここから全射・単射・全単射は、核と像の一致による図式で説明できました。
今後$0_{1},0_{2}$は省略して「$0 \to $」や「$\to 0$」と書きます。
2.一般の図式で…
1.では一つの線形写像に注目した図式でしたが、複数個つなげるとどうでしょう。
ただの$R$線形写像$f \in \mathrm{Hom}_{R}(M,N)$について次の$2$本の像と核が一致する図式ができます。
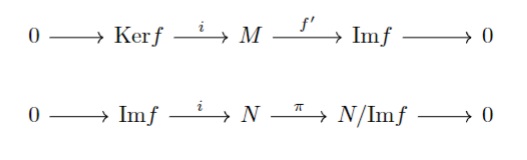
$f’$は値域が像に制限しているので、$if’=f$となるようにしています。
今$\mathrm{Im}f=\mathrm{Ker}\pi$ですね。
そうするとこの2本の図式は、左右で繋げられそうです。
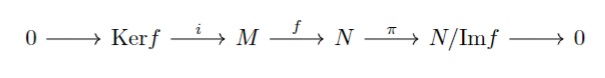
確かに像と核が一致しています。
- 包含写像$i$は単射($\mathrm{Ker}i=\{0_{M}\}$), $\mathrm{Im}i=\mathrm{Ker}f$,
- $\mathrm{Im}f=\mathrm{Ker}\pi$,
- $\pi$は全射($\mathrm{Im}\pi=\{0_{N}\}$)
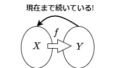
これを繰り返すことで次のような隣接する線形写像の像と核が一致し続ける列が取れます。
これが一般の完全列です。
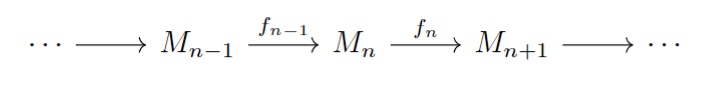
- すべての$n$で$\mathrm{Ker}f_{n}=\mathrm{Im}f_{n-1}$.
もちろん逆に無限に続く像と核の一致し続ける列に対し、像と核で短い列に分解できます。
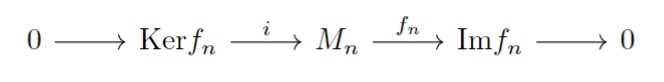
- $i$は包含写像, $f_{n}(n \in \mathbb{Z})$は像集合に制限した$f_{n}$,
- $i$は単射($\mathrm{Ker}i=\{0_{M}\}$), $\mathrm{Im}i=\mathrm{Ker}f_{n}$,
- $f_{n}$は全射($\mathrm{Im}f_{n}=\{0_{M_{n+1}}\}$)
定義 完全列
導入で議論した用語を整理しましょう。
$R$:環 $\{M_{n}\}_{n \in \mathbb{Z}}$:$R$加群の集合族
$\{f_{n}:M_{n} \to M_{n+1}\}$:$R$線形写像の族
$(*):\mathrm{Im}f_{n}=\mathrm{Ker}f_{n+1}(n \in \mathbb{Z})$
次の図式を$l$とおく.
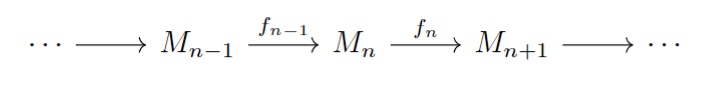
$l$は$R$加群の完全列$(\rm{exact \; sequence}) \overset{def}{\iff} l$は$(*)$を満たす.
次の$R$加群$L,M,N$と$R$線形写像$f,g$からなる図式$l’$を取る.
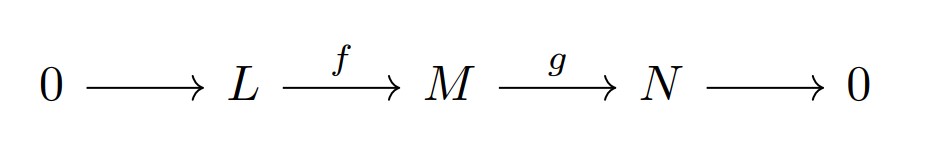
$l’$は短完全列$\overset{def}{\iff} f:$単射, $g:$全射,$\mathrm{Ker}g=\mathrm{Im}f$.
導入で構成した完全列は短い完全列をつなぎ合わせて作っていました。
これは、左右に無限に伸びる完全列に対しても同様の方法で説明できます。
$R$環上の加群の族$\{M_{n}\}_{n \in \mathbb{Z}}$、$R$線形写像の族$\{f_{n}:M_{n} \to M_{n+1}\}$を取る.
このとき以下互いに同値である.
(1)次の図式は完全列である.
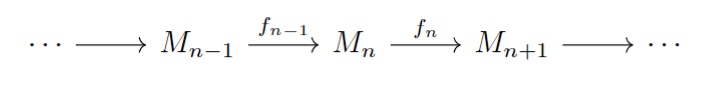
(2)任意の$n \in \mathbb{Z}$に対し, 次は短完全列である.
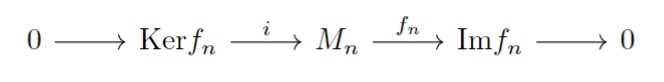
証明は、導入の議論を添字ごとに行うだけです。
基本的に完全列が与えられた場合、短完全列に分解して考察します。
特に分解した際に現れる像と核は、特定の加群の特徴を表すものにありえます。
(ホモロジー代数では特定の状況で”syzygy”などと呼ばれます。)
おわりに
学習帳ではすでにいくつかの主張やその利用を考察しています。
基本性質は、ホモロジー代数ではなく加群で証明するのでそちらで取り上げた主張もおいおい。
以上、ケンけんでした。