こんにちは!ケンけんです。
今回は、加群を調べるにあたり強力な道具である直和とより広い直積を取り扱います。
キーワード:加群の直積・直和
この記事では、環$R$を単位的可換環として$R$加群を取ります。
導入
集合の直積と言えば、座標平面のように成分を並べた元からなる集合でした。(参考)
そしてその和やスカラー倍は高校数学で既に定義したことがありますね。
そう、ベクトルです。
高校でのベクトルは向きと絶対値を持つ量でしたが和とスカラー倍は次のように定義していました。
- 和:$(x,y)+(z,w)=(x+z,y+w)(x,y,z,w \in \mathbb{R})$
- スカラー倍:$r(x,y)=(rx,ry)(r,x,y \in \mathbb{R})$
線形代数を知っているなら、これは$V=\mathbb{R}^{2}$の$\mathbb{R}$ベクトル空間としての和とスカラー倍を定義していると分かるでしょう。
演算の構成自体は、各成分ごとに和とスカラー倍を定義しているだけです。
これをそのまま加群の直積集合に使えば線形代数からの拡張として定義できそうです。
定義 加群の直積と直和
それでは定義しますが、直積の他にもう一つの主題も一気に書いてしまいます。
$\Lambda$:添え字集合 $\{M_{\lambda}\}_{\lambda \in \Lambda}$:$R$加群の族
$\Pi_{\lambda \in \Lambda}M_{\lambda }=\{(x_{\lambda})|\forall \lambda \in \Lambda, x_{\lambda} \in M_{\lambda}\}$
(添字集合がわかる場合は$\Pi_{\lambda}M_{\lambda} $と略します)
$\bigoplus_{\lambda \in \Lambda}M_{\lambda }=\{(x_{\lambda}) \in \Pi_{\lambda \in \Lambda}M_{\lambda }|\text{有限個の}\lambda \text{を除き}x_{\lambda}=0\}$
(添字集合がわかる場合は$\bigoplus_{\lambda}M_{\lambda} $と略します)
$\Pi_{\lambda \in \Lambda}M_{\lambda }$は次の演算により$R$加群となる.
- 和 :$\Pi_{\lambda \in \Lambda}M_{\lambda} \times \Pi_{\lambda \in \Lambda}M_{\lambda} \to \Pi_{\lambda \in \Lambda}M_{\lambda }(((x_{\lambda}),(y_{\lambda})) \mapsto (x_{\lambda}+y_{\lambda}))$
- 作用:$R \times \Pi_{\lambda \in \Lambda}M_{\lambda} \to \Pi_{\lambda \in \Lambda}M_{\lambda}((r,(x_{\lambda})) \mapsto (rx_{\lambda}))$
- $\Pi_{\lambda \in \Lambda}M_{\lambda}$:$\{M_{\lambda}\}_{\lambda \in \Lambda}$の直積($\rm{direct \; product}$)
- $\bigoplus_{\lambda \in \Lambda}M_{\lambda}$:$\{M_{\lambda}\}_{\lambda \in \Lambda}$の直和($\rm{direct \; sum}$)
- 各$\lambda$で$M_{\lambda}$は$\bigoplus_{\lambda \in \Lambda}M_{\lambda}$の直和因子($\rm{direct \; summand}$)
- $\bigoplus_{\lambda \in \Lambda}M_{\lambda} $は$ \Pi_{\lambda \in \Lambda}M_{\lambda}$の部分加群
元が直積集合なので例えば次のような成分ごとの包含写像と射影が存在します。
$\{M_{\lambda}\}_{\lambda \in \Lambda}$を$R$加群の族とする.
$\delta_{\lambda,\nu}=\begin{cases}1_{R} & \text{if} \lambda= \nu\\ 0_{R} & \text{if} \lambda \neq \nu\end{cases} $
(1)$i_{\lambda’}:M_{\lambda’} \to \Pi_{\lambda \in \Lambda}M_{\lambda}(m \mapsto (\delta_{\lambda’,\nu}m))$は単射$R$線形写像,
(2)$p_{\lambda’}:\Pi_{\lambda \in \Lambda}M_{\lambda} \to M_{\lambda’}((m_{\lambda} \mapsto m_{\lambda})$は全射$R$線形写像,
$i_{\lambda’}$は$\lambda’$成分への埋め込み, $p_{\lambda’}$は$\lambda’$成分の射影と呼ぶ.
成分ごとの比較なので、証明は省略します。
これら2つは添字集合が非加算集合または加算無限集合ならば、違う対象です。
有限集合の場合は、直和の定義を直積も満たせてしまうので同じように扱います。
$$\Pi_{i=1}^{n}M_{i}=\bigoplus_{i=1}^{n}M_{i}$$
普遍性から見た加群の直積と直和
どこを見てもほぼ差がない直積と直和ですが、実は次の性質からその差を感じられます。
$\{M_{\lambda}\}_{\lambda \in \Lambda}$を$R$加群の族とする.
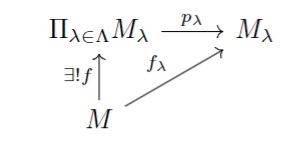
(1)任意の$R$加群$M$と各$\lambda$に対し, $f_{\lambda}:M \to M_{\lambda}$を取る.
このとき, 各$\lambda$で$p_{\lambda}f=f_{\lambda}$を満たす$f \in \mathrm{Hom}_{R}(M,\Pi_{\lambda \in \Lambda}M_{\lambda})$がただ一つ存在する.
つまり, 以下の図式を可換にする$f$がただ一つ存在する.($p_{\lambda}$は$\lambda$成分の射影)
(2)任意の$R$加群$M$と各$\lambda$に対し, $g_{\lambda}:M_{\lambda} \to M$を取る.
このとき, 各$\lambda$で$g_{\lambda}=gi_{\lambda}$を満たす$g \in \mathrm{Hom}_{R}(\bigoplus_{\lambda \in \Lambda}M_{\lambda},M)$がただ一つ存在する.
つまり, 以下の図式を可換にする$g$がただ一つ存在する.($i_{\lambda}$は包含写像)
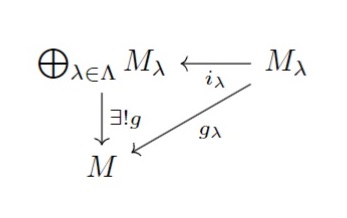
$f:M\to \Pi_{\lambda \in \Lambda}M_{\lambda}(m \mapsto (f_{\lambda}(m)))$と定義する.
well-defindと$R$線形性は成分ごとに比較するため, 各$f_{\lambda}$から従う.
任意の$m \in M$に対し, $p_{\lambda}f(m)=p_{\lambda}((f_{\lambda}(m)))=f_{\lambda}(m)$より可換である.
次に$p_{\lambda}h=f_{\lambda}$を満たす$h \in \mathrm{Hom}_{R}(M,\Pi_{\lambda \in \Lambda}M_{\lambda})$を取り$h=f$を示す.
任意の$m \in M$に対し, $f(m)=(f_{\lambda}(m))$であり$h(m)=(y_{\lambda})$とおく.
各$\lambda$で$f_{\lambda}=p_{\lambda}f=p_{\lambda}h$より, $f_{\lambda}(m)=y_{\lambda}$となる.
従って$h(m)=(f_{\lambda}(m))=f(m)$となり$h=f$である.
$\square$
直和の方はかなり大変なのでパートごとに分けます。
任意の$(x_{\lambda}),(y_{\lambda’}) \in \bigoplus_{\lambda \in \Lambda}M_{\lambda}$に対し,
$i=1,\ldots,n,j=1 ,\ldots , m$で$x_{\lambda_{i}}\neq 0, y_{\lambda’_{j}}\neq 0$, それ以外を$0$とする.
$g:\bigoplus_{\lambda \in \Lambda}M_{\lambda} \to M((x_{\lambda}) \mapsto \sum_{\lambda \in \Lambda}g_{\lambda}(x_{\lambda}))$と定義する.
$x_{\lambda_{i}}\neq 0(i=1,\ldots, n)$それ以外で$0$より有限和$\sum_{i=1}^{n}g_{\lambda_{i}}(x_{\lambda_{i}})$が取れる.
$g_{\lambda_{i}}$のwell-definedから, $(x_{\lambda})=(x’_{\lambda})$ならば各$\lambda$で$g_{\lambda}(x_{\lambda})=g_{\lambda}(x’_{\lambda})$である.
従って, $\sum_{i=1}^{n}g_{\lambda_{i}}(x_{\lambda_{i}})=\sum_{i=1}^{n}g_{\lambda_{i}}(x’_{\lambda_{i}})$から, $g$はwell-definedである.
任意の$\lambda \in \Lambda$で$x \in M_{\lambda}$に対し,
$gi_{\lambda}(x)=g(\delta_{\lambda,\lambda’}x)=g_{\lambda}(x)$.
従って, $gi_{\lambda}=g_{\lambda}$である.
作用について$r \in R$に対し,
$rg((x_{\lambda}))=r(\sum_{i=1}^{n}g_{\lambda_{i}}(x_{\lambda_{i}}))=\sum_{i=1}^{n}g_{\lambda_{i}}(rx_{\lambda_{i}}))=g((rx_{\lambda}))=g(r(x_{\lambda}))$.
加法について, $\lambda_{i}=\lambda’_{j}$とする$\lambda$は$m+n$個以下より,
$i=1,\ldots , l \leq m+n$で$x_{\lambda_{k}} \neq 0,y_{\lambda_{k}} \neq 0$と並び変える.
次に, $i=n-l,\ldots, n$に対し$x_{\lambda_{i}} \neq 0, y_{\lambda_{i}}=0$,
$j=m-l, \ldots , m$に対し$x_{\lambda’_{j}} = 0, y_{\lambda’_{j}} \neq 0$として,
$\lambda’_{j}=\lambda_{n+j}$で$i=1, \ldots, m+n-l$で並べ替える.
これにより, $x_{\lambda_{i}}+y_{\lambda_{i}} \neq 0$となりえるように取り換えられた.
従って,
$\begin{align} g((x_{\lambda})+(y_{\lambda})) &= \sum_{i=1}^{m+n-l}g_{\lambda_{i}}(x_{\lambda_{i}}+y_{\lambda_{i}})\\ &= \sum_{i=1}^{m+n+l}g_{\lambda_{i}}(x_{\lambda_{i}})+\sum_{i=1}^{m+n+l}g_{\lambda_{i}}(y_{\lambda_{i}})\\ &=g((x_{\lambda}))+g((y_{\lambda})).\end{align}$
以上から, $g$は$R$線形写像である.
各$\lambda$で$g’i_{\lambda}=g_{\lambda}$を満たす$g’:\bigoplus_{\lambda \in \Lambda}M_{\lambda} \to M$を取る.
任意の$(x_{\lambda}) \in \bigoplus_{\lambda \in \Lambda}M_{\lambda}$について,
$i=1,\ldots, n$で$x_{\lambda_{i}}\neq 0$, それ以外の成分を$0$とする.
このとき, $(x_{\lambda})=\sum_{i=1}^{n}i_{\lambda_{i}}(x_{\lambda_{i}})$と書ける.
$g’i_{\lambda}=g_{\lambda}=gi_{\lambda}$から, 次のように$g=g’$が示される.
$g'((x_{\lambda}))=\sum_{i=1}^{n}g’i_{\lambda_{i}}(x_{\lambda})=\sum_{i=1}^{n}gi_{\lambda_{i}}(x_{\lambda})=g((x_{\lambda}))$.
$\square$
この性質が、直積と直和を分ける一つの条件となっています。
図式を見ればわかるように、ちょうど写像の方向を全て逆にした形になっています。
実はこの命題は圏論的直積・直和の定義を具体的にしたものになっています。
例えば直積は、MOD1-8-3(1)を満たす$(\Pi_{\lambda}M_{\lambda},p_{\lambda})$のことを指します。
(この$\Pi_{\lambda}M_{\lambda},p_{\lambda}$は条件を満たす対象と写像で上で定義したものとは限りません)
また、この対象は同型(今だと$R$加群としての同型で)を許すと一つに決まります。
MOD1-8-3のような「一意的」な情報を使って定義される道具・用語をよく「普遍性」と呼びます。
以前の誘導写像や準同型定理もその一つです。
逆に今回のように具体的な直積集合から定義することを「構成的」と呼ぶことがあります。
(こちらはマイナーなのかあまり聞きません)
そして、直積よりも直和が使いやすいのはMOD1-8-3(2)の加群へ写像を伸ばせる点です。
実は直積では、大抵写像を伸ばせません。
直和の証明を見ると分かるように、非零な成分が有限個だから各成分の像の和で定義できます。
同じことを直積ですると、無限個の和を考える必要があります。
当然位相を付けていない加群では、無限和など考えられません。
そのため、直和で成り立つが直積では成り立たない性質が多く存在します。
おわりに
いまだに直和の写像の確認でもっと完結な表現が見つかりません。(特に加法)
ちなみに直積でうまくいかせる方法(無限和をできるようにする)が完備化になります。
そちらはおいおい…
少々冗長な説明になってしまいましたが、うまい表現を見つけたらまた更新したいです。
以上、ケンけんでした。