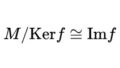こんにちは!ケンけんです。
今回は、生成されたイデアルの拡張である生成された部分加群を取り扱います。
キーワード:生成された部分加群・有限生成加群
この記事では、環はすべて単位的可換環とし$R$加群として環$R$上の加群とみなします。
導入・定義 生成された部分加群
動機づけとしては、生成されたイデアルと全く同じと考えてもいいです。
つまりは、骨組み(必要な部品)だけで「生成」された部分加群を考えるだけです。
骨組みだけでは、演算構造が怪しいのでそれを覆うように最低限の元を取って加群にするわけです。
図:骨組みのイメージ
なので早速定義します。
$M$:$R$加群 $S \subset M$ $\Sigma_{M}$:$M$の部分加群全体の集合
$X=\{N \in \Sigma_{M}|S \subset N\}$
$(S)=\bigcap _{N \in X}N$:$S$により生成される部分加群($\rm{an \; module \; generated \; by \; S}$)
$S$は$(S)$の生成系($\rm{generated \; system}$), その元を生成元($\rm{generator}$)と呼ぶ.
特に$S=\{s_{1}, \ldots , s_{m}\}$のとき, $(S)=(s_{1}, \ldots , s_{m})$と書く.
$N \in \Sigma_{M}$に対し,
$N$は有限生成($\rm{finitely \; generated} $) $\overset{def}{\iff} M$は有限集合な生成系を持つ.
$N=(m)(m \in M)$のとき, $N$は$m$による巡回加群($\rm{cyclic \; module}$)と呼ぶ.
イデアルを加群に置き換えただけなので、納得できると思います。
イデアルと同様に、$(S)$は$S$を含む最小の部分加群であることが共通部分からわかります。
例としては、次のように単純なものがいくつもあります。
- 環$R$自身がイデアルとして$(1_{R})$より有限生成
- 多項式環$R[X]$を$R$加群とみなすと, $S=\{1,X,X^{2}, \ldots, X^{n}, \ldots\}$により生成される.
- $\mathbb{Z}$加群として$\mathbb{Z}/n\mathbb{Z}=(\overline{1})$で有限生成.
イデアルと同様に生成系による様々な表示があります。
$M$を$R$加群とし, $S \subset M$を取る.
(1)$(S)=\{\sum_{i=1}^{n}r_{i}s_{i}|r_{i} \in R, s_{i} \in S\}$,
(2)$S=\{s_{i}|i=1,\ldots, m\} \Rightarrow (S)=\sum_{i=1}^{m}Rs_{i}$.
$Y=\{\sum_{i=1}^{m}r_{i}s_{i}|m \in \mathbb{N}, r_{i} \in R, s_{i} \in S, i=1, \ldots , m\}$とおく.
各$s \in S$について$1_{R} s=s \in Y$より$S \subset Y$である.
加法と作用が明らかより$Y$が$M$の部分加群となる.
従って, $(S)$の最小性から$(S) \subset Y$である.
逆は, 各部分加群$S \subset N \subset M$について$Y \subset N$を示せば十分である.
任意の$x=\sum_{i=1}^{m}r_{i}s_{i} \in Y(m \in \mathbb{N}, r_{i} \in R, s_{i} \in S)$について$r_{i}s_{i} \in N$となる.
以上から, $x \in N$のため$Y \subset (S)$となる.
$\square$
$(1)$より$(S)=\{\sum_{i=1}^{m}r_{i}s_{i}|r_{i} \in R\}$と書ける.
従って, $Z=\{\sum_{i=1}^{m}r_{i}s_{i}|r_{i} \in R\}$とおき, $Z=\sum_{i=1}^{m}Rs_{i}$を示せば十分である.
部分加群の和から, $\sum_{i=1}^{m}Rs_{i}=\{\sum_{i=1}^{m}a_{i}|a_{i} \in Rs_{i}\}$である.
ここで各$x \in (s_{i})$は, $x=r_{i}s_{i}(r \in R)$と書けるため, $\sum_{i=1}^{m}Rs_{i}=\{\sum_{i=1}^{m}r_{i}s_{i}|r_{i} \in R\}=Z$となる.
$\square$
有限生成の場合、生成系の濃度は自然数値しかとらないため必ず最小数が存在します。
(有限全順序集合は最小元・最大元を持つ。)
生成系と基底
イデアルと部分加群ではそれぞれ、有限生成性に価値があります。
今回の部分加群の場合は、線形代数での基底が思い出されます。
頻繁に扱う$k$上の有限次元ベクトル空間$V$は次元個の基底を持ちました。
つまり$V$は有限生成$k$加群だといえます。
基底の特徴はいくつかありますが、環上の加群としては次の$2$点でしょう。
- 空間を生成するための最小の個数$=$次元個
- 線形独立性
次元個より少ない元でベクトル空間は生成できないため、最小の生成系の濃度になります。
線形独立性は、「線形結合が$0 \Rightarrow $各係数は$0$」でした。
これらの条件を環上の加群にも拡張したいわけです。
しかしこれには壁がいくつもあります。
例えばそのまま線形独立性の条件を環に持ち込むと、次のような反例が存在します。
$\mathbb{Z}$加群として$\mathbb{Z}/4\mathbb{Z}$を見る.
- $\mathbb{Z}/4\mathbb{Z}=(\overline{1})$,
- $4 \cdot \overline{1}=\overline{0}$.
- よって$\overline{1}$は線形独立を満たせない.
一つの元でもできない場合が存在する時点で、一般的には成り立たないと分かります。
また生成系の最小の濃度も怪しいです。
基底の存在と数が一定か不明なので、ベクトル空間の方法では次元が定義できないからです。
このように結局「基底の存在と数の一定性」に依存していることになります。
環上の加群では、これらを別々の性質を見ることで解決することができます。
ベクトル空間では、「基底の個数」と「生成系の最小の濃度」が結果的に同じ性質だと説明できます。
それぞれ次へ議論が派生していきます。
- 基底とその一定性$\Rightarrow$ 自由加群
- 有限生成加群での生成系の極小(最小)の濃度$\Rightarrow$ 局所環上の有限生成加群
自由加群はあらゆる加群と関連付けられる加群の中で最もきれいな加群だといえます。
(ベクトル空間にかなり近く任意の環で考えられる。)
一方環を局所環に制限を掛けた2点目は、かなり環側の性質に依存した性質になります。
加群論では、多くの性質が$2$点目の加群を中心としているほど良い性質を持つわけです。
おわりに
今回は、イデアルのほぼ焼き直しなのでそちらを知っていると真新しさが薄くなっています。
今後の展開を少し紹介した形になりますが、順次追加していきます。
以上、ケンけんでした。