こんにちは!ケンけんです。
今回は合同式の一般化である剰余環およびイデアルの対応を取り扱います。
キーワード:剰余環
この記事では、環はすべて単位的可換環とします。
導入
高校での整数問題では、よくあまりに注目した議論がありました。
倍数ごとの余りに着目して「$\equiv$」で結ぶ式を合同式と呼んでいました。
指導範囲外のため必ず学ぶわけではないですが、教科書などで参考に乗っているはずです。
このあまりごとに着目する手法、集合の同値関係に似ていますね。
$2$つの整数$x,y$が整数$n$で割ったあまりが一致するとき、その差が$n$の倍数になります。
例えば$4$を法とする合同式では、余りが$1$で一致する$5,9$で次のように書いていました。
$$5 \equiv 9(\rm{mod} \; 4)$$
特に余りの計算は、和や積も反映されています。
($x=an+b,y=cn+d$のとき、$x+y \equiv b+d, xy=bd(\rm{mod} \; n)$となるように。)
少し示してみましょう。
$n$を整数として次のように$\mathbb{Z}$上に関係を作る.
$x \equiv y \overset{def}{\iff} x-y \in (n)$
(1)$\equiv$は$\mathbb{Z}$上の同値関係である,
商集合$(\mathbb{Z}/\equiv)=\mathbb{Z}/n \mathbb{Z}$と書く.
(2)$\overline{x}=[x] \in \mathbb{Z}/n \mathbb{Z}$と書く.
- 加法:$\overline{x}+\overline{y}\overline{x+y}$,
- 乗法:$\overline{x}\overline{y}=\overline{xy}$.
$\mathbb{Z}/n \mathbb{Z}$は1.2.の加法・乗法により環をなす.
(1)任意の整数$x,y,z$を取る.
$x-x=0 \in (n)$より$x \equiv x$である.
$x \equiv y$ならば, $x-y \in (n)$より$-(x-y)=y-x \in (n)$のため$y \equiv x$である.
$x \equiv y,y \equiv z$ならば, $x-y,y-z \in (n)$である.
よって, $x-z=(x-y)+(y-z) \in (n)$で$x \equiv z$である.
従って$\equiv$は$\mathbb{Z}$上の同値関係である.
(2)演算のwell-definedを確認すれば十分である.
任意の$\mathbb{Z}/n \mathbb{Z}$元で$\overline{x}=\overline{x’},\overline{y}=\overline{y’}$を仮定すると,
$x-x’,y-y’ \in (n)$である.
$(x+y)-(x’+y’)=(x-x’)+(y-y’) \in (n)$である.
$y(x-x’),x'(y-y’) \in (n)$から,
$xy-x’y’=y(x-x’)+x'(y-y’) \in (n)$である.
以上から, $\overline{x+y}=\overline{x’+y’},\overline{xy}=\overline{x’y’}$でwell-definedである.
$\square$
あまりだけに注目した合同式は実際には、整数環の商集合が再び環でその演算に従っています。
「整数から割ったあまりに着目する」は、集合を絞って商集合で考える動機に合致しています。
これを$\mathbb{Z}$から一般の環に置き換えたものが剰余環です。
定義 剰余環
それでは命題とともに定義します。
$R$を環とし, $I \subset R$をイデアルとする.
(1)次の$R$上の関係は同値関係である.
$x \sim y \overset{def}{\iff} x-y \in I$.
$(R/\sim)=R/I$, $\overline{x}=[x] \in R/I$と書く.
(2)$R/I$は次の加法と乗法で環をなす.
- $+:R/I \times R/I \to R/I((\overline{x},\overline{y}) \mapsto \overline{x+y})$
- $\bullet:R/I \times R/I \to R/I((\overline{x},\overline{y}) \mapsto \overline{xy})$
$R/I$を$I$による$R$の剰余環($\rm{quotient \; ring}$)と呼ぶ.
実は導入の整数環の命題は集合とイデアルの性質しか使っていないためそのまま一般化できます。
(なので証明はBR1-9-1を参照)
剰余環は、とてもきれいな全射環準同型写像を構成できよく「自然な準同型」と呼ばれます。
$R$を環とし, $I$をそのイデアルとする.
(1)$\pi:R \to R/I(x \mapsto \overline{x})$は全射環準同型写像である.
(2)$\mathrm{Ker}\pi=I$.
(1)well-definedは明らかで, 環準同型性は$R/I$の演算が$R$で説明できるため従う.
よって全射性を確認すれば十分であるが,
任意の$\overline{x} \in R/I$を取ると, $x \in R$より$\pi(x)=\overline{x}$と表せる.
よって全射である.
(2)任意の$x \in \mathrm{Ker}\pi$を取ると, $\pi(x)=\overline{x}=\overline{0}$である.
よって, $x=x-0 \in I$から$\mathrm{Ker}\pi \subset I$.
任意の$x \in I$に対し, $x=x-0 \in I$より$\pi(x)=\overline{x}=\overline{0}$.
従って$I \subset \mathrm{Ker}\pi$となる.
$\square$
イデアル対応と素イデアル
さて全射環準同型写像が常に構成できることがわかったので、少し比較の話題を挙げてみます。
それは次のイデアル対応原理です。
$R$を環とし, $\sum_{R}$を$R$のイデアル全体の集合とする.
$I \in \sum_{R}$を取る.
$X=\{J \in \sum_{R}|I \subset J \}$とおく.
このとき, $X$と$\sum_{R/I}$は次の写像により包含関係を保つ一対一対応する.
$\Phi:X \rightarrow \sum_{R/I}(J \mapsto \pi(J))$
$\Psi:\sum_{R/I} \rightarrow X(J’ \mapsto \pi^{-1}(J’))$
($\pi:R \rightarrow R/I$は自然な準同型)
これは$R/I$のイデアルは、$R$のイデアル$J$で$J/I$と記述できることを示しています。
特に、素イデアル・極大イデアルについても少し変えることで一対一対応が得られます。
(この主張含めすべてこの記事でまとめています。)
包含関係を保つこの対応から、極小素イデアルのより一般的な表記が出てきます。
素イデアルでの対応を利用するため、参考記事から系を持ってきます。
$R$を環とし, $\mathrm{Spec}R$を$R$の素イデアル全体の集合とする.
$I \subset R$をイデアルとして$\mathcal{V}(I)$を次のように定義する.
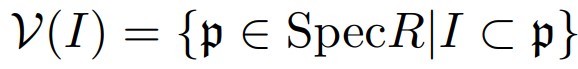
このとき, $\mathcal{V}(I)$と$\mathrm{Spec}(R/I)$は次の写像により包含関係を保つ一対一対応する.
$\Phi:\mathcal{V}(I) \rightarrow \mathrm{Spec}(R/I)(\mathfrak{p} \mapsto \pi(\mathfrak{p}))$
$\Psi:\mathrm{Spec}(R/I) \rightarrow \mathcal{V}(I)(\mathfrak{p’} \mapsto \pi^{-1}(\mathfrak{p’}))$
($\pi:R \rightarrow R/I$は自然な準同型)
$R$を環, $I$をそのイデアルとする.
$\mathrm{Min}I$と$\mathrm{Min}R/I$は一対一対応する.
系2の対応は包含を保つため極小元が極小元に対応する.
$\mathrm{Min}I$は$\mathcal{V}(I)$の極小元の集合, $\mathrm{Min}R/I$は$\mathrm{Spec}R/I$の極小元の集合である.
$\mathcal{V}(I)$と$\mathrm{Spec}R/I$の対応から, $\mathrm{Min}I$と$\mathrm{Min}R/I$は一対一対応する.
$\square$
書籍によって、$\mathrm{Min}I$と$\mathrm{Min}R/I$で表記ブレがあるのはこんな理由があったわけです。
おわりに
合同式と剰余環は高校数学からつながるため、特定の条件で見る対象を減らす商集合の利用として最も理解しやすい部類だと思います。
また極小素イデアルの表記は、加群論からも上の説明で同一視することが説明できます。
そちらで触れた際に再度考察します。
以上、ケンけんでした。