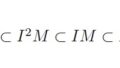今回ほぼ線形代数…
こんにちは!ケンけんです。
今回は、加群準同型写像を取り扱います。
代数系の基礎導入はどれも同じですがしっかりやっていきますよ。
キーワード:加群準同型写像(線形写像)
この記事では、$R$加群と書き単位的可換環$R$上の加群とします。
導入
構造を保つ写像を群・環・体・加群それぞれで準同型写像と呼びます。
その導入は次の点で分けて考えると見通しがいいです。
- 定義域の加群構造で像集合を加群にできる.
- 像集合が値域の部分加群になる.
必要なことを挙げてみます。
設定として$f:M \to N$を環$R$上の加群の写像とします。
1.(像集合の加群構造は定義域の構造に従う)
- $x,y \in M \Rightarrow f(x)+f(y)=f(x+y)$.
- 左辺(“$f(M)$”の加法)を右辺(“$M$”の加法)で定義する.
- $x \in M, r \in R \Rightarrow rf(x)=f(rx)$.
- 左辺(“$f(M)$”のスカラー倍)を右辺(“$M$”のスカラー倍)で定義する.
任意の$f(M)$の元は$f(x),f(y)(x,y \in M)$の形で加群構造が定義できています。
2.(像集合が値域の部分加群)
- $f(x),f(y) \in f(M) \Rightarrow f(x)+f(y) \in f(M)$.
- ある$z \in M$で$f(x)+f(y)=f(z)$とできる.
- $f(x) \in f(M), r \in R \Rightarrow rf(x) \in f(M)$.
- ある$w \in M$で$rf(x)=f(w)$とできる.
こちらは$N$の演算と像集合の定義から必要な条件となります。
注意:1.と2.の加群構造は次のように定義は違います。
- $f(M)$に$M$の演算で演算を定義している.
- $N$の演算で$f(M)$の条件を説明している.
しかし、1.は2.の条件も満たすため1.と2.を合わせた次の条件を採用します。
- $f(x),f(y) \in f(M) \Rightarrow f(x)+f(y) =f(x+y)$,
- $f(x) \in f(M), r \in R \Rightarrow rf(x) =f(rx)$.
それぞれ左辺($N$の演算)を右辺($M$の演算)で説明できています。
これで$f$は「像集合を定義域と同じ構造の部分加群にする写像」と特徴づけることができます。
定義
定義は加群準同型写像と線形写像を統一するため、係数の環を強調し線形写像と呼びます。
(基本どちらでも問題ありません。)
$M,N$:$R$加群 $f:M \to N$:写像
$(1) m,n \in M \Rightarrow f(m+n) =f(m)+f(n)$
$(2)m \in M,r \in R \Rightarrow f(rm) =rf(m) $
$f$:$R$線形写像($\rm{linear \; map}$)$\overset{def}{\iff} f$は$(1),(2)$を満たす.
$\mathrm{Hom}_{R}(M,N)$と書き, $M$から$N$への$R$線形写像全体の集合とする.
単射のときはモノ($\rm{monomorphism}$),
全射のときはエピ($\rm{epimorphism}$)と呼ぶことがある.
もちろん係数を環から体にすることで線形代数での線形写像と同じです。
この$\mathrm{Hom}_{R}(M,N)$は$M,N$とは別に加群になります。(参考)
導入で挙げた像集合は確かに値域の部分加群となります。
$M,N$を$R$加群, $f:M \to N$を$R$線形写像とする.
このとき, $f(M)$は$N$の部分加群である.
$f(M)$は像集合より空集合ではない.
$n,n’ \in f(M),r \in R$に対し, $n+n’, rn \in f(M)$を確認する.
ある$m,m’ \in M$により$f(m)=n,f(m’)=n’$と書けるため,
$n+n’=f(m+m’) \in f(M), rn=f(rm) \in f(M)$となる.
$\square$
この定義により零元の対応などが決まります。
$M,N$を$R$加群, $f:M \to N$を$R$線形写像とする.
(1)$f(0_{M})=0_{N}$
(2)$m \in M \Rightarrow f(-m)=-f(m)$,
(1) $0_{f(M)}=0_{N}$より$f(M)$の元で零元となることを確認する.
任意の$n=f(m) \in f(M)$に対し,
$f(m)=f(m+0_{M})=f(m)+f(0_{M})=f(0_{M})+f(m)$.
従って$f(0_{M}) =0_{f(M)}$である.
(2)任意の$m \in M$に対し,
$0_{N}=f(0_{M})=f(m-m)=f(m)+f(-m)$,
から$-f(m)=f(-m)$となる.
$\square$
像と核, 同型
ここからは、線形写像を通した加群の比較に触れます。
まず次の主張が成り立ちます。
$M,N$を$R$加群, $f:M \to N$を$R$線形写像とする.
(1)$\mathrm{Im}f=f(M)$は$N$の部分加群である,
(2) $\mathrm{Ker}f=\{m \in M|f(m)=0\}$は$M$の部分加群である.
$\mathrm{Im}f$を$f$の像($\rm{image}$), $\mathrm{Ker}f$を$f$の核($\rm{kernel}$)と呼ぶ.
像についてはすでに確認したので、核について示します。
$f(0_{M})=0_{N}$から, $0_{M} \in \mathrm{Ker}f \neq \emptyset$である.
任意の$m,n \in \mathrm{Ker}f$に対し, $f(m)=f(n)=0$である.
従って, $r \in R$について
$f(m+n)=f(m)+f(n)=0, f(rm)=rf(m)=0$から
$m+n,rm \in \mathrm{Ker}f$となる.
以上から, $\mathrm{Ker}f$は$M$の部分加群である.
$\square$
これらは、単射・全射を特徴づけるツールになります。
$M,N$を$R$加群, $f:M \to N$を$R$線形写像とする.
(1)$f$は単射$ \iff \mathrm{Ker}f=\{0\}$,
(2)$f$は全射$ \iff \mathrm{Im}f=N$.
これも全射は定義そのままなので単射だけ確認します。
(1) $\Rightarrow$について,
$\mathrm{Ker}f \subset \{0\}$を示せば十分である.
任意の$x \in \mathrm{Ker}f$に対し$f(x)=f(0_{M})=0_{N}$である.
$f$の単射性から$x=0_{M}$より$\mathrm{Ker}f \subset \{0\}$である.
$\Leftarrow$について,
$m,m’ \in M$に対し$f(m)=f(m’)$を仮定する.
このとき, $f(m-m’)=0_{N}$から$m-m’ \in \mathrm{Ker}f$より$m=m’$で$f$は単射である.
$\square$
最後に全単射な線形写像の特徴付けを取り上げます。
$M,N$を$R$加群, $f:M \to N$を$R$線形写像とする.
このとき, 以下は互いに同値である.
(1)$f$は全単射である,
(2)$f$は$R$線形写像となる逆写像を持つ.
全単射な線形写像を同型写像($\rm{isomorphism}$)と呼ぶ.
どちらもほぼ同じですが、書籍によっては(2)で記述しています。
この命題は全単射の確認で十分だということを主張しています。
$(1) \Rightarrow (2)$の$g=f^{-1}$が$R$線形写像となることを示す.
任意の$n,n’ \in N$に対し,
$f$の全射性から$n=f(m),n’=f(m’)(m,m’ \in M)$と表せる.
従って, $g$の加法は次のように定義される.
$\begin{align*}g(n+n’) &= g(f(m)+f(m’))\\ &=g(f(m+m’))=m+m’\\ &=gf(m)+gf(m’)\\ & =g(n)+g(n’). \end{align*}$
また作用も次のように定義される.
$\begin{align*}g(rn) &= g(f(rm))\\ &= rm=r(gf(m))\\ &= rg(n). \end{align*}$
以上から, $g$は$R$線形写像である.
$(2) \Rightarrow (1)$については、逆写像が存在するため明らかである.
$\square$
なぜ全単射だけでなく逆写像に線形性も付けた方が定義とされているのでしょう。
すぐ後に上の命題を示してしまうため、実用性も考えると全単射だけでいい気がします。
1.加群の中で考えると…
「加群構造を比較する」意図を見せるためと考えることができます。
「同型」の意味を考えると、定義域と値域の加群構造(型)が同じだといえるでしょう。
つまり$f:M \to N$によって
- $N=\mathrm{Im}f$の構造を$M$の構造で説明,
- $M=\mathrm{Im}f^{-1}$の構造を$N$の構造 で説明.
という意味を込めると, 線形写像になる逆写像といった方が意味合いが強く感じられます。
2.はみ出して圏論まで行くと…
ここからは少しはみ出して圏論での事情を深入りせず言葉だけで挙げてみます。
まず重要な事実として加群がなす圏は様々な場所で利用する典型的な圏の例です。
そして圏論では、逆写像に対応する「逆射($\rm{inverse}$)」は存在します。
これを使って$\rm{isomorphism}$が定義されます。
しかし、集合論でいうところの単射・全射は一般的に存在せず、代わりに$\rm{monomorphism}$と$\rm{epimorphism}$が存在します。
圏を集合の範囲に狭めることで、$\rm{monomorphism}$が単射、$\rm{epimorphism}$が全射の条件に言い換えられなじみのある性質になるのです。
そして$\rm{mono}$かつ$\rm{epi}$(全単射)だからといって$\rm{iso}$とは限りません。
(集合論での議論ができないため)
つまり最終的な拡張先である圏論で考えると、集合論の言葉でしかない全単射ではなく逆写像による$\rm{isomorphism}$で説明した方が正しい!!…ということなんでしょうか。
おわりに
余談ですが、洋書を読むようになると和訳の用語たちに少しずれを感じるようになりました。
例えば「準」同型写像ならば$\rm{quasi \text{-} isomorphism}$の方が正しいように感じます。
別だと準正則という用語は$\rm{quasi \text{-} regular}$としっかり準($\rm{quasi \text{-}}$)を接頭語に着けています。
概念理解でも英語の方が意味をとらえているのでこっちで理解した方がいいかもしれません。
以上、ケンけんでした。