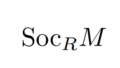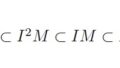多分構造本体が中心の代数学だと一番話題の範囲と拡張性が広いのではなかろうか。
こんにちは!ケンけんです。
今回は、環上の加群の導入記事です。
環上とあるように、環の知識は仮定します。(こちら)
キーワード:環上の加群
必須知識:環の定義
補助知識:群・イデアルの定義
注意:この記事での環は可換とは限りません。
導入
高校数学のベクトルと言えば、加法とスカラー倍を満たす数と向きを持つ量でした。
線形代数だと、これが集合の元と演算に置き換わりベクトル空間と呼ばれる対象に一般化されます。
環上の加群は、このスカラー倍が環の元($\mathbb{Z}$など)に変わっただけです。
一般化で得られるものはないように見えますが、かなり違います。
- 基底が定まらない
- なのでベクトル空間での次元がそのまま一般化できない。
- 線形写像のような行列表示が難しい。
- $0$以外のスカラー倍でも$0$になる可能性がある
- (のスカラー倍だと逆元を作用させることで元に戻せるから存在しない。)
- 状況によって作用の方向を区別する必要がある
適当にこれだけ並べられます。
「基底」と「次元」が使えないので、線形代数の主張の多くで別方法を考えなければいけません。
また、一般化することでベクトル空間の性質を同値な主張に言いかえできるかわかります。
また環自身が加群のため、加群での性質を使って逆に環を調べることもできます。
(可換環論だと多い手法)
線形代数の一般化だけど「一般の場合はできることが限られる対象」と考えばいいと思います。
定義する前に、説明上加法群のために群を挙げておきます。
$G$:集合 $\cdot :G \times G \rightarrow G((x,y) \mapsto x \cdot y)$:写像
(1)$l,m,n \in G \Rightarrow l \cdot (m \cdot n)=(l \cdot m) \cdot n$(加法の結合律),
(2)$\exists 1_{G} \in G \forall m \in M s.t. 1_{G} \cdot m=m \cdot 1_{G}=m$(零元の存在),
(3)$\forall x \in G \exists y \in G s.t. \; x \cdot y=y \cdot x=1_{G}$(逆元の存在),
(4)$\forall x,y \in G(x \cdot y=y \cdot x)$(可換律).
写像$\cdot$は$G$の積$\overset{def}{\iff} \cdot$は(1)を満たす.
$G$は群$\overset{def}{\iff} G$は(1)-(3)を満たす.
特に(4)も満たす場合, $G$はアーベル群(または可換群)と呼ぶ.
整数と同様の加法を標準の加法とすると、(1)-(4)すべて満たすのでアーベル群を構成できます。
(中学数学で学ぶ演算規則の確認そのもの)
加法群は、標準の加法を群の積とする群のことです。
細かくは群の記事で示しますが、単位元は唯一なので$1$や加法群の場合は$0$と書きます。
ということで、次節で定義に入っていきましょう。
定義 環上の加群
それでは定義します。
$R$:環 $M$:加法群
左作用:$l:R \times M \rightarrow M(l(r,m)=rm)$
(1)$m,n \in M,r \in R \Rightarrow r(m+n)=rm+rn$,
(2)$m \in M,r,s \in R \Rightarrow (r+s)m=rm+sm$,
(3)$m \in M,r,s \in R \Rightarrow (rs)m=r(sm)$,
(4)$m \in M \Rightarrow 1_{R} m=m$.
$M$は左$R$加群($\rm{left}$ $R$ $\rm{module}$) $\overset{def}{\iff} M$は(1)-(4)を満たす.
どの性質も、線形代数のベクトル空間の定義そのままです。
スカラー倍の元が、$\mathbb{R}$や$\mathbb{C}$のような体ではないだけです。
可換環上の加群と作用
初めに注意書きでデカデカと書いたように環の可換性は加群に影響を与えます。
先の定義では「左」作用とあるので右作用も考えられます。
$R$:環 $M$:加法群
右作用:$r:M \times R \rightarrow M(r(m,t)=mt)$
(1)$m,n \in M,r \in R \Rightarrow (m+n)r=mr+nr$,
(2)$m \in M,r,s \in R \Rightarrow m(r+s)=mr+ms$,
(3)$m \in M,r,s \in R \Rightarrow m(rs)=(mr)s$,
(4)$m \in M \Rightarrow m 1_{R} =m$.
$M$は右$R$加群($\rm{right}$ $R$ $\rm{module}$) $\overset{def}{\iff} M$は(1)-(4)を満たす.
本当に$R$の元を左右で書く場所を置き換えただけに見えます。
置き換えただけなので左加群なら、右加群と言える…わけではありません。
もちろん、成り立つ場合もありますが基本的には別物として扱います。
ただし、可換環上の場合は別です。
$R$を可換環とし, $M$を加法群とする.
- $M$は左$R$加群である$\iff M$は右$R$加群である.
従って, 左右を無視して$M$を単に$R$加群と呼ぶ.
$M$を左$R$加群とする.
今, 写像$r: M \times R \rightarrow M((m,t) \mapsto tm)$と定義する.
任意の$m,n \in M, s,t \in R$を取り1-1-2の(1)-(4)を確認すれば十分である.
$(m+n)s=s(m+n)=sm+sn=ms+ns$,
$m(s+t)=(s+t)m=sm+tm=ms+mt$,
$m(st)=(st)m=(ts)m=t(sm)=(sm)t=(ms)t$,
$m 1_{R}=1_{R}m=m$.
従って $M$は$r$によって右$R$加群となる.
右$R$加群を仮定した場合も同様である.
$\square$
作用の結合律で、左右の作用させる順序で環の可換性が必要になっています。
以上から、可換環上では左右無視して議論ができます。
加群の性質の多くは、「左加群を左加群」「右加群を右加群」に移ります。
なので、あまり気にしないですが可換環上だとそんな心配もありません。
(可換環上で成り立つことは、たいていは一般の環上でも成り立ちます。)
ベクトル空間の場合に左右を考えてなかったのも、スカラー倍が体(つまり可換環)だったためです。
例
例としては次のものがあります。単純化のためすべて可換環にします。
- 環$R$のイデアル$I$:$R$加群
- 環$R$自身:$R$加群
- 多項式環$R[X]$:$R$加群
- アーベル群$G$:$\mathbb{Z}$加群($r \in \mathbb{Z},m \in G$に対し$\sum_{i=1}^{r}m=rm$と和の個数表示で定義)
- 剰余環$R/I$:$R$加群,$R/I$加群
おわりに
導入単品だとこんなにあっさりした内容に…
定義だけなら線形代数の知識+$\alpha$の知識だけなのでこのようになりました。
しばらくは、線型代数と変わらない内容が続くと思います。
以上、ケンけんでした。