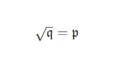soc(M) の「socle」は「一番底」を指すらしい….
こんにちは!ケンけんです。
今回は、ホモロジー代数の影響で時々現れるsocleという加群についての記事になります。
それでは行ってみよう!
キーワード:加群の礎石(socle)
前提知識:$\mathrm{Hom}$関手の性質(この記事とか)
この記事では、環はすべて単位的可換環とします。
定義 Soc(M)
まず、話の中心にある$\mathrm{Soc}M$がどのような集合かを定義します。
$(R,\mathfrak{m},k)$:局所環 $M$:$R$-加群
$\mathrm{Soc}_{R}(M)=\mathrm{Hom}_{R}(k,M)$:$M$の砥石($\rm{Socle}$)
構成から, $\mathfrak{m} \subset \mathrm{Soc}_{R}(M)$より$k$線形空間ともみなせます。
$\mathrm{Soc}_{R}(M)$は、環に条件を付けると非自明な場合を作ることができます。
例えば、Artin局所環$(R,\mathfrak{m},k)$の場合は非零な加群$M$について$\mathrm{Ass}_{R}M=\{\mathfrak{m}\}$です。
従って、非自明な単射$k \rightarrow M$が存在し$\mathrm{Hom}_{R}(k,M) \neq (0)$です。
今回のこの記事は、次の2点を目標とします。
- $\mathrm{Soc}_{R}M$の別表示
- $\mathrm{Soc}_{R}M$の一般的な性質の整理
$\mathrm{Soc}_{R}M$の別表記
$\mathrm{Hom}_{R}(-,-)$なので、別表記がイメージしずらいですが実はとても単純になります。
$(R,\mathfrak{m},k)$を局所環とし, $0 \neq M$を$R$加群とする.
- $\mathrm{Soc}_{R}M \cong (0:_{M}\mathfrak{m})$
言いかえ先の$(0:_{M}\mathfrak{m})$は別記事で取り上げた「$\rm{colon \; submodule}$」です。
簡略化のため$\overline{1_{R}}=1,\overline{0_{R}}=0$と書く.
任意の$f \in \mathrm{Hom}_{R}(k,M)$について$f(1)=x \in M$が定まる.
また, 任意の$m \in \mathfrak{m}$に対し$mx=mf(1)=f(\overline{m})=f(0)=0$である.
従って, $x \in (0:_{M}\mathfrak{m})$より$F:\mathrm{Soc}_{R}M \rightarrow (0:_{M}\mathfrak{m})(f \mapsto x)$が定義できる.
任意の$f,g \in \mathrm{Soc}_{R}M$と$r \in R$について, $f(1)=x,g(1)=y$とおく.
このとき, 次のようにして$F$は$R$線形写像であることが示される.
$F(f+g)=(f+g)(1)=f(1)+g(1)=x+y=F(f)+F(g)$,
$F(rf)=(rf)(1)=rx=rF(f)$.
$F$が全単射であることを示す.
$\mathrm{Hom}_{R}(R,M) \cong M$の対応から, 次の$R$線形写像が得られる.
$\mu:(0:_{M}\mathfrak{m}) \rightarrow \mathrm{Hom}_{R}(R,M)(a \mapsto (\mu(a):r \mapsto ra))$
$\mathfrak{m} \subset \mathrm{Ker}\mu(a)$より, $\widetilde{\mu(a)}:k \rightarrow M$を誘導し, $f=\widetilde{\mu(a)}$とすると$F(f)=a$である.
よって, $F$は全射である.
単射については, $\mathrm{Ker}F \subset \{0\}$を示せば十分である.
$f \in \mathrm{Ker}F$を取ると, $F(f)=f(1)=0$より$f$が零写像となる.
よって $f=0$である.
$\square$
場合によっては、$(0 :_{M} \mathfrak{m})$で定義することもあります。
その他の諸性質
ここからは、一般の局所環上でのsocleで満たすことを整理していきます。
$(R,\mathfrak{m},k)$を局所環とし, $M,M_{i}(i \in I)$を$R$加群とする.
$N,P\subset M$を部分加群とする.
(1)$\mathrm{Soc}_{R}M \subset M$,
(2)$\mathrm{Soc}_{R}(\mathrm{Soc}_{R}M)=\mathrm{Soc}_{R}M$,
(3)$\mathrm{Soc}_{R}M \cap N=\mathrm{Soc}_{R}N$,
(4)$N \subset P \Rightarrow \mathrm{Soc}_{R}N \subset \mathrm{Soc}_{R}P$.
(5)$\mathrm{Soc}_{R}(\Pi_{i \in I}M_{i})=\Pi_{i \in I} \mathrm{Soc}_{R}M_{i}$
(1),(3),(4)は$\mathrm{Soc}_{R}M=(0:_{M}\mathfrak{m})$で考えると明らかである.
(2)$\mathrm{Hom}$と$\otimes$の随伴性より, $\mathrm{Hom}_{R}(k,\mathrm{Hom}_{R}(k,M))) \cong \mathrm{Hom}_{R}(k \otimes_{R}k,M)=\mathrm{Hom}_{R}(k,M)$である.
従って, $\mathrm{Soc}_{R}(\mathrm{Soc}_{R}M)=\mathrm{Soc}_{R}M$である.
(5)は$\mathrm{Hom}_{R}(k, \Pi_{i}M_{i}) \cong \Pi_{i}\mathrm{Hom}_{R}(k,M_{i})$から従う.
$\square$
おわりに
多分追記します。(決定事項)
本当は、NoetherやArtin局所環の特殊な場合の例を挙げるつもりがうまく説明できないのでとりあえずここまでで出しました。
うなってるとずっとまとめができないので現段階で確定した部分だけ放出しました。
以上、ケンけんでした。