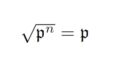こんにちは!ケンけんです。
今回は、分解の中心となる準素イデアルを取り扱います。
キーワード:準素イデアル
導入
始めるにあたって、まずは素因数分解をイデアルに書き表してみます。
正の整数$a \in \mathbb{Z}$について「有限個の素数の積で一意的に書ける。」が主張でした。
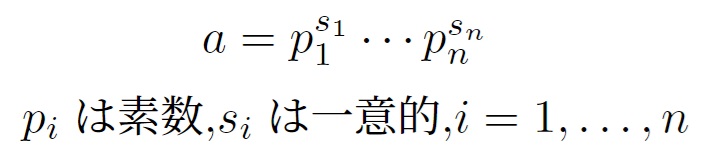
集合の元レベルで見るとここで終わりです。
これを集合のイデアルで考えれば、集合での分割も考えることができます。
単項イデアル$I=(a)$を考えると次のことがわかります。
$\mathbb{Z}$を整数環, $a=p_{1}^{s_{1}} \cdots p_{n}^{s_{n}}$を正の整数とする.
$I=(a)=(p_{1})^{s_{1}} \cdots (p_{n})^{s_{n}}=\bigcap_{i=1}^{n}(p_{i})^{s_{i}} $
$I=(p_{1}^{s_{1}} \cdots p_{n}^{s_{n}})=(p_{1})^{s_{1}} \cdots (p_{n})^{s_{n}}$は集合の一致を示すだけなので明らかである.
素数の性質から$i\neq j $について$p_{i}$と$p_{j}$は互いに素である.
従って, $(p_{1})^{s_{1}} \cdots (p_{n})^{s_{n}}=\bigcap_{i=1}^{n}(p_{i})^{s_{i}}$である.
$\square$
互いに素なイデアルの性質なども使いました。
(有限個の互いに素なイデアルでは、「イデアルの共通部分」$=$「イデアルの積」)
一般の集合用語である共通部分の方が、積より単純なのでこちらを使っていきます。
さて、素数による単項イデアル$(p_{i})$は素イデアルでした。
しかし、そのべき乗$(p_{i})^s_{i}$は素イデアルではありません。
例えば$P=(p_{i})^2$について、$(p_{i})^2 \in P$だが$p_{i} \notin P$です。
また、$(p_{i})^s_{i}=\bigcap_{j=1}^{s_{i}}(p_{i})$は素数$p_{i}$自身とは互いに素でないためできません。
なので、共通部分で扱う場合はべき乗のままで使います。
定義 準素イデアル
それでは定義していきます。
$R$:環 $\mathfrak{q} \subset R$:イデアル
$\mathfrak{q}$:準素イデアル($\rm{primary \; ideal}$)$\overset{def}{\iff} \forall x,y \in R(xy \in \mathfrak{q} \Rightarrow (x \in \mathfrak{q}) \vee (y \in \sqrt{\mathfrak{q}}))$
条件式は、素イデアルのものが根基イデアルに取り変わっています。
導入において、準素イデアルは素数のべきに対応するとありました。
イデアルのべきについては、根基イデアルの元で説明できます。
ここから、素イデアルと根基の性質を持ちそうであると想像できます。
実際に、次のように準素イデアルは特徴づけることができます。
$R$を環とする.
(1)$\mathfrak{q} \subset R$:準素イデアル$\Rightarrow \sqrt{\mathfrak{q}} \in \mathrm{Spec}R$,
(2) $P \in \mathrm{Spec}{R} \Rightarrow P$:準素イデアル.
(1)$x,y \in R$について「$(xy \in \sqrt{\mathfrak{q}}) \wedge (x \notin \sqrt{\mathfrak{q}}) \Rightarrow y \in \sqrt{\mathfrak{q}}$」を示せば十分である.
$xy \in \sqrt{\mathfrak{q}}$から, ある$n >0$で$(xy)^n=x^n y^n \in \mathfrak{q}$である.
$x \notin \sqrt{\mathfrak{q}}$から,$x^n \notin \mathfrak{q}$でもあるため$y^n \in \sqrt{\mathfrak{q}}$である.
従って, $m >0$で$(y^n)^m=y^{mn} \in \mathfrak{q}$である.
以上より, $y \in \sqrt{\mathfrak{q}}$である.
(2)$P \in \mathrm{Spec}R$について
$\sqrt{P}=P$より, 準素イデアルの条件式は$P$が素イデアルである条件式そのものである.
以上から, $P$は準素イデアルである.
根基イデアルは、元になるイデアルの極小素イデアルの共通部分でした。
つまり次の2つの議論で、$\mathrm{Min}\mathfrak{q}=\{\sqrt{\mathfrak{q}}\}$となります。
- $\mathfrak{q} \subset \sqrt{\mathfrak{q}}$より$\sqrt{\mathfrak{q}} \in \mathcal{V}(\mathfrak{q})$,
- 各$P \in \mathrm{Min}\mathfrak{q}$で$\sqrt{\mathfrak{q}}=\bigcap_{P’ \in \mathrm{Min}\mathfrak{q}}P’ \subset P$.
このことから$\mathfrak{p}=\sqrt{\mathfrak{q}}$として, 準素イデアル$\mathfrak{q}$は「$\mathfrak{p}$-準素イデアル」と呼ばれます。
導入で挙げた素イデアルのべきが準素イデアルなのか確認してみましょう。
$p$を素数として$P=(p)$を$\mathbb{Z}$の素イデアルとする.
このとき, $n>0$に対して$P^n=(p^n)$である.
- $a=p_{1}^{s_{1}} \cdots p_{m}^{s_{m}},b=q_{1}^{r_{1}} \cdots q_{n}^{r_{n}}$を正の整数とする.
- (負の場合は($-1$)を掛けるだけなので正の場合を調べれば十分.)
- $ab \in P^n$を仮定すると,$p^n$を因数に持つ.
- $a \notin P^n$の場合, $p$を素因数に持たない,または$p^i(i <n)$を因数に持つ.
- $a$が$p$を素因数に持たない場合, $b$が$p^n$を因数に持つ.
- $\Rightarrow b \in P^n$.
- $a$が$p^i(i <n)$を因数に持つ場合, $b$は$p^{n-i}$を因数に持つ.
- $\Rightarrow b^t \in P^n$.($(t(n-i) \geq n$を満たす$t$について)
- $P^n$は$P$-準素イデアルである.($\sqrt{P^n}=P$より)
(途中の$t>0$の存在はアルキメデスの原理で保障されます。)
素イデアルより緩い準素イデアル
一連の主題である準素イデアルは、条件式などからもわかります。
その上で、さらに包含関係についても一般化されています。
例えば、次の共通部分です。
$R$を環とし, $\mathfrak{q}_{1},\mathfrak{q}_{2} \subset R$を$\mathfrak{p}$-準素イデアルとする.
このとき, $\mathfrak{q}_{1} \cap \mathfrak{q}_{2}$は$\mathfrak{p}$-準素イデアルとなる.
$x,y \in R$に対して$xy \in \mathfrak{q}_{1} \cap \mathfrak{q}_{2}, x \notin \mathfrak{q}_{1} \cap \mathfrak{q}_{2}$を仮定する.
$xy \in \mathfrak{q}_{1}$かつ$xy \in \mathfrak{q}_{2}$である.
$x$について$x \notin \mathfrak{q}_{1}$または$x \notin \mathfrak{q}_{2}$である.
$\mathfrak{q}_{1}$が準素イデアルより, $x \notin \mathfrak{q}_{1}$ならば$y \in \sqrt{\mathfrak{q}_{1}}=\mathfrak{p}=\sqrt{\mathfrak{q}_{2}}$である.
根基の性質より, $\sqrt{\mathfrak{q}_{1} \cap \mathfrak{q}_{2}}=\sqrt{\mathfrak{q}_{1}} \cap \sqrt{\mathfrak{q}_{2}}=\mathfrak{p}$である.
よって, $y \in \sqrt{\mathfrak{q}_{1} \cap \mathfrak{q}_{2}}$である.
$x \notin \mathfrak{q}_{2}$の場合も同様に$y \in \sqrt{\mathfrak{q}_{1} \cap \mathfrak{q}_{2}}$が得られる.
以上から, $\mathfrak{q}_{1} \cap \mathfrak{q}_{2}$は$\mathfrak{p}$-準素イデアルである.
$\square$
一般の素イデアルの場合、共通部分は「包含関係がある」ほど強いものに限られました。
準素イデアルならば、根基が一致していれば包含関係なしに共通部分でも保ってくれます。
この事実は後々重要になってきます。
おわりに
分解のパーツとなる準素イデアルですが、他にも素イデアルより広くイデアルの操作が可能です。
そちらは別枠で取り上げたいです。
次回は、準素分解とその最短性を取り上げます。
以上、ケンけんでした。