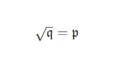こんにちは！ケンけんです。
今回は、多項式の根（方程式の解）らしき元の集合「根基イデアル」を取り扱います。
キーワード：根基イデアル
この記事では、環はすべて単位的可換環とします。
構成 根基イデアル
まずは、根基イデアルがどのようなものなのかはっきりさせます。
そしてここで注意ですが、この記事での「環」はすべて「単位的可換環」とします。
$R$：環 $I \subset R$：イデアル
$\sqrt{I}=\{x \in R|\exists n > 0 \; s.t. \; x^n \in I\}$：$I$の根基イデアル($\rm{radical \; ideal}$).
イデアルと呼んでいるこの集合ですが、これがイデアルであるかは確認が必要です。
$R$を環とし, $I \subset R$をイデアルとする.
このとき, $\sqrt{I}$はイデアルである.
また, $\sqrt{I}=\bigcap_{P \in \mathcal{V}(I)}P$と表せる.
方針としては直接証明と素イデアルの共通部分表記を示す2つあります。
$\mathcal{V}(I)$についてはこちらを。（セットで読めるようにしました。）
今回はどちらも提示します。
可換環が二項定理を満たすことを利用する.
まず, $\emptyset \neq I \subset \sqrt{I}$である.
任意の$x, y \in \sqrt{I}$を取ると, ある$m,n >0$で$x^m,y^n \in I$である.
従って, $(x+y)^{m+n}=\sum_{i=0}^{m+n}$ $ _{m+n}C_{i}x^{m+n-i}y^{i}$である.
$m+n-i \geq m$ならば, $x^{m+n-i} \in I$である.
$m+n-i <m$ならば, $n <i$より$y^{i} \in I$である.
以上から, $(x+y)^{m+n} \in I$より$x+y \in \sqrt{I}$である.
また, 任意の$x \in \sqrt{I},r \in R$についてある$m >0$で$(rx)^m=(r^m)(x^m) \in I$である.
よって, $rx \in \sqrt{I}$となり$\sqrt{I}$はイデアルである.
$\square$
$\sqrt{I} \subset \bigcap_{P \in \mathcal{V}(I)}P$について
任意の$x \in \sqrt{I}$を取ると, ある$m>0$で$x^m \in I \subset P(P \in \mathcal{V}(I))$である.
従って, 各$P \in \mathcal{V}(I)$について$x^n \in P \Rightarrow x \in P$である.
よって, $x \in \bigcap_{P \in \mathcal{V}(I)}P$である.
逆の包含について
$x \in \bigcap_{P \in \mathcal{V}(I)}P$で$x \notin \sqrt{I}$を満たす元の存在を仮定し矛盾を導く.
まず, 包含関係による半順序集合$T=\{J \subset R|I \subset J:イデアル, x \notin \sqrt{J}\}$を取る.
この集合は、整列集合である真のイデアル全体$\Sigma$の部分集合である.
また, $I \in T$であるため$T \neq \emptyset$である.
よって, 任意の全順序部分集合$S \subset T$は上界$J=\bigcup_{J’ \in S}J’$を$\Sigma$の中で持つ.
各$J’ \in S$について, $I \subset J’$かつ$x \notin \sqrt{J’}$である.
従って, $I \subset J$かつ$x \notin \sqrt{J}$より$S$の$T$での上界となる.
従って, Zornの補題から$T$が極大元を持ち$P$と置く.
次に, 極大元$P$が素イデアルであることを示す.
$a,b \notin P$を仮定すると, $P \subsetneq P+(a), P+(b)$となる.
$P$の極大性と, $I \subset P$より$x \in \sqrt{P+(a)},x \in \sqrt{P+(b)}$である.
十分大きな$n >0$により, $x^n=p+ka,x^n=q+lb(p,q \in P, k,l \in R)$と書ける.
従って, $x^{2n}=(pq+plb+qka)+klab$となる.
$ab \in P$の場合, $x^{2n} \in P$から$x \in \sqrt{P}$である.
しかし, $P \in T$に矛盾するため$ab \notin P$である.
よって, $I \subset P$は素イデアルであり$x$の取り方から$x \in P$である.
しかし, $P \in T$より$f \notin \sqrt{P}$に矛盾する.
以上より, 仮定した$x$が存在せず$\bigcap_{P \in \mathcal{V}(I)}P \subset \sqrt{I}$である.
イデアルの共通部分はイデアルより, $\sqrt{I}=\bigcap_{P \in \mathcal{V}(I)}P$はイデアルである.
$\square$
2つ目の証明では、素イデアルの共通部分から根基への包含は直接証明が難しいです。
極大ではみ出る部分を使う「対象（集合でも元でも）」の存在証明は時々現れます。
「十分大きな$n >0$」は、$x^l \in P+(a) ,x^m \in P+(b)$となる$l,m$の最大値です。
根基の性質
べきで特徴づく根基がイデアルとなるため、イデアル（集合らしい）等号を考えたいです。
実際に、$\sqrt{-}$での中身のイデアルの包含や操作をある程度外に出せます。
$R$を環とし, $I,J \subset R$をイデアルとする.
(1)$I \subset \sqrt{I}$,
(2)$\sqrt{\sqrt{I}}=\sqrt{I}$,
(3)$I \subset J \Rightarrow \sqrt{I} \subset \sqrt{J}$,
(4)$\sqrt{I} \cap \sqrt{J} =\sqrt{IJ}=\sqrt{I \cap J}$.
(1)
元そのものが$I$の元より明らかである.
(2)
(1)から$\sqrt{I} \subset \sqrt{\sqrt{I}}$である.
任意の$x \in \sqrt{\sqrt{I}}$についてある$m,n >0$で$x^m \in \sqrt{I},(x^m)^n \in I$である.
従って, $x \in \sqrt{\sqrt{I}}$である.
(3)
任意の$x \in \sqrt{I}$について, ある$n>0$で$x^n \in I \subset J$より$x \in \sqrt{J}$である.
(4)
$\sqrt{I} \cap \sqrt{J} \subset \sqrt{IJ} \subset \sqrt{I \cap J} \subset \sqrt{I} \cap \sqrt{J}$で示す.
任意の$x \in \sqrt{I} \cap \sqrt{J}$について, ある$m,n>0$で$x^m \in I,x^n \in J$である.
従って, $x^{mn}=(x^m)(x^n) \in IJ$より$x \in \sqrt{IJ}$である.
$x \in \sqrt{IJ}$について, $IJ \subset I \cap J$と(3)から$\sqrt{IJ} \subset \sqrt{I \cap J}$である.
任意の$x \in \sqrt{I \cap J}$について, ある$n>0$で$x^n \in I \cap J$である.
よって, $s \in \sqrt{I} \cap \sqrt{J}$である.
$\square$
素イデアルによる表示は次の主張の確認を元の確認なしで説明できます。
$R$を環とし, $P \in \mathrm{Spec}R$とする.
$\sqrt{P}=P$,
より一般に, 任意の$n >0$に対して, $\sqrt{P^n}=P$.
$\mathrm{Min}P=\{P\}$より, 任意の$Q \in \mathcal{V}(P)$について$P \subset Q$である.
従って, $\sqrt{P}=P$である.
任意の$n>0$に対して, BR1-6-3(4)より$\sqrt{P^n}=\bigcap_{i=1}^{n}\sqrt{P}=P$である.
$\square$
また、$\sqrt{-}$の中身を零イデアル$(0)$とした特別な根基も存在します。
$R$：環
$N(R)=\sqrt{0}=\bigcap_{P \in \mathrm{Spec}R}P$：$R$のべき零根基（$\rm{nilradical}$）
極小素イデアルとのつながり
さて、素イデアルによる表示は、別の視点を与えてくれます。
共通部分による表記は、「包含関係の極小元」に簡略化できる点です。
$R$を環とし, $I \subset R$をイデアルとする.
$\sqrt{I}=\bigcap_{P \in \mathrm{Min}I}P$.
包含関係は小さい部分集合に制限できるので、証明は自然です。
ここから、$\mathrm{Min}I$を調べることは根基である程度分かるといえます。
例えば、根基$\sqrt{I}$が極大イデアル$M$の場合は$\mathrm{Min}I=\{M\}$となります。
（この場合、$I$は自動的に準素イデアルと呼ばれる特殊なイデアルになります。）
また、極大ではない素イデアル$P$の場合でも$\mathrm{Min}I=\{P\}$となります。
おわりに
実は、根基の素イデアル表示証明はべき零根基での論法を一般化したものです。
[1]では先に剰余環も扱い、べき零根基と組み合わせた議論で話が進んでいました。
この場合、証明中の部分集合$T$が$T=\{J \subset R|J:$イデアル,$x \notin \sqrt{J} \}$になります。
ただ、その後の操作は同様であり剰余環なしで証明できるので採用しました。
（べき零根基からの説明はサブで挙げます。）
以上、ケンけんでした。
参考文献
[1]M.F.Atiyah, I.G.Macdonald, Introduction to Commutative Algebra, Addison-Wesley Publishing Co., Reading, Mass.-London-Don Mills,Ont.1969
