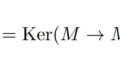こんにちは!ケンけんです.
最近可換代数の学習で平坦性をやってるんですが,まぁテンソル積を使うわけです.
そして,線形写像$f$の像と核を平然とテンソル積と順序交換しています.
これではダメだということで,どんな時に像や核を取る操作とテンソル積が交換できるのかを言語化目的で記事にします.
それでは行ってみよう!
キーワード:テンソル積
この記事では,環を単位的可換環とします.
テンソル積の像と核
まず,今回の主題を明確にします.
$R$を環とし,$M, N, P$を$R$加群,$f \in \mathrm{Hom}_{R}(M,N)$を取る.
$f_{P}=f \otimes 1:M \otimes_{R}P \rightarrow N \otimes_{R} P(m \otimes p \mapsto f(m) \otimes p)$と定義する.
(1)$\mathrm{Im}f \otimes_{R}P \cong \mathrm{Im}f_{P}$
(2)$\mathrm{Ker}f \otimes_{R} P \cong \mathrm{Ker}f_{P}$
- これらが成り立つ条件は何か?
一見あたりまえにみえますが,テンソル積の線形性が結構な悪さをします.
(ある意味テンソル積の面倒な点をよく表す部分)
その基準として,$\rm{divisible \; module}$による影響があります.
$R$を環とし,$M$を$\rm{divisible}$ $R$加群とする.
このとき,各$R$のイデアル$I$について次が成り立つ.
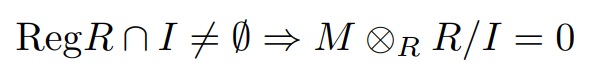
$\mathrm{Reg}R \cap I \neq \emptyset$より, ある正則元$r$で$r \in I$となる.
$M$がdivisibleより,各$m \in M$について$m=rm’$とする$m’ \in M$が存在する.
したがって,任意の$m \otimes \overline{a} \in M \otimes_{R}R/I$について
$m \otimes \overline{a}=rm’ \otimes \overline{a}=m’ \otimes r \overline{a}=m’ \otimes 0=0.$
以上から,$M \otimes_{R} R/I=\{0\}$である.
$\square$
単純な反例として次のものがあります.
$\mathrm{Im}f \otimes_{R}P = \mathrm{Im}f_{P}$.
(反例)$R,M=\mathbb{Z}, N=\mathbb{Q},P=\mathbb{Z}/p\mathbb{Z}$($p$は素数).
$f : M \rightarrow N$(包含写像).
$\mathbb{Q}$はdivisible moduleより,$N \otimes_{R}P=0$.
よって$\mathrm{Im}f_{P}=\{0\}$だが,$\mathrm{Im}f \otimes_{R}P=\mathbb{Z} \otimes_{R}P \cong P \neq \{0\}$となる.
$\mathrm{Ker}f \otimes_{R} P = \mathrm{Ker}f_{P}$.
(反例)$R=\mathbb{Z}, M=\mathbb{Q}, N=\mathbb{Q}/\mathbb{Z},P=\mathbb{Z}/p\mathbb{Z}$($p$は素数).
$f : M \rightarrow N$(自然な準同型).
$\mathbb{Q}$はdivisible moduleより,$M \otimes_{R}P=0$.
よって$\mathrm{Ker}f_{P}=0$だが,$\mathrm{Ker}f \otimes_{R}P=\mathbb{Z} \otimes_{R}P \cong P \neq \{0\}$となる.
このように,一般の場合は反例ができてしまいます.
でも、書籍ではしれっとこの交換を利用しているケースがある.
それは,大抵は平坦性を利用しています.
平坦性
平坦性は,同値命題についての性質ですが次の形が最もわかりやすいです.
$R$を環とし,次の列を$R$加群と準同型がなす完全列とする.
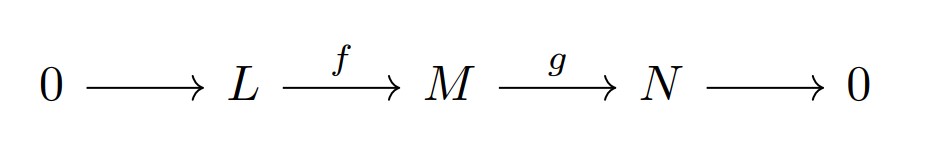
$P$を$R$加群とする.
$P$は平坦加群$\overset{def}{\iff}$ 次の列は完全列である.
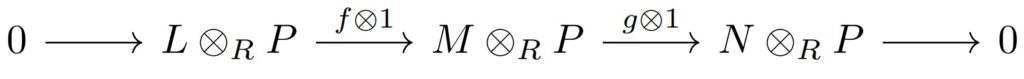
($f\otimes 1$が単射になることはテンソル積では自明ではない.)
テンソル積は$\mathrm{Hom}$関手の逆で右完全性を持っています.
そのため,全射は明らかですが単射は平坦性が必要になります.
$R$を環とし,$M, N, P$を$R$加群,$f \in \mathrm{Hom}_{R}(M,N)$を取る.
$f_{P}=f \otimes 1:M \otimes_{R}P \rightarrow N \otimes_{R} P(m \otimes p \mapsto f(m) \otimes p)$と定義する.
(1)$f$は全射 $\Rightarrow $ $f_{P}$は全射である.
特に,$\mathrm{Im}f_{P} \cong N \otimes_{R}P=\mathrm{Im}f \otimes_{R}P$である.
(2)$f$は単射 かつ $P$は平坦加群 $\Rightarrow $ $f_{P}$は単射.
特に, $\mathrm{Ker}f_{P} = \{0\} =\mathrm{Ker}f \otimes_{R}P$である.
この場合は単純に,像や核が加群で表現できるので$\otimes_{R}$と$\mathrm{Im},\mathrm{Ker}$を取る操作が可換になっています.
この場合は極端すぎるので,もっと広げられないかと考えました。
$f$に単射や全射を課さずに$\otimes_{R}$と$\mathrm{Im},\mathrm{Ker}$を取る操作が可換になる例はあるか?
追記:2025/1/16 平坦性のみで成り立ちます!!!
$R$を環とし,$M, N$を$R$加群,$F$を平坦加群とし,
$f \in \mathrm{Hom}_{R}(M,N)$を取る.
$f_{F}=f \otimes 1:M \otimes_{R}F \rightarrow N \otimes_{R} F(m \otimes x \mapsto f(m) \otimes x)$と定義する.
このとき,次が成り立つ.
(1)$\mathrm{Im}f_{P} \cong \mathrm{Im}f \otimes_{R}P$.
(2)$\mathrm{Ker}f_{P} \cong \mathrm{Ker}f \otimes_{R}P$.
(1)$f$を自明な全射$f’:M\to \mathrm{Im}f$と単射$i:\mathrm{Im}f \to N$の合成に分解する.
$F$の平坦性から,$f’\otimes_{R}1_{F}, i \otimes_{R}1_{F}$はそれぞれ全射,単射である.
よって,$\mathrm{Im}f \otimes_{R}F \cong \mathrm{Im}(i \otimes_{R}1_{F})$である.
以上から,次の同型が得られる.
$\begin{align*} \mathrm{Im}f_{F}&= \mathrm{Im}((i\otimes_{R}1_{F}) \circ (f’\otimes_{R}1_{F}))\\ &=\mathrm{Im}(i\otimes_{R}1_{F}) \cong \mathrm{Im}f \otimes_{R}F. \end{align*}$
(2)次の自明な完全列を取る.
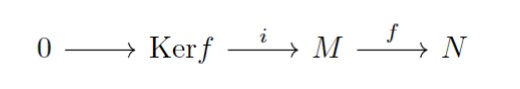
$F$の平坦性から,次の完全列が得られる.

$i\otimes 1_{F}$は単射より,$\mathrm{Ker}f \otimes_{R}F \cong \mathrm{Im}(i\otimes 1_{F})$である.
また完全性から,$\mathrm{Ker}f \otimes_{R}F \cong \mathrm{Ker}f_{F}$が得られる.
$\square$
得られた例(平坦加群すべて)
考えた例と言いたいところですが,一般で成り立つため簡単な局所化を挙げておきます.
問題となる点は次のことです.
- 部分加群(像や核)のテンソル積は,元のテンソル積に単射を伸ばせるか?
これは,平坦性によって解決できるのでした.これをうまく使います.
環$R$と積閉集合$S$について$R_{S}$は平坦$R$加群になります.
(参考:局所化の完全性と同型$M\otimes_{R}R_{S} \cong M_{S}$から)
$R$をとし, $M, N$を$R$加群, $f \in \mathrm{Hom}_{R}(M,N)$とする.
$f_{R_{S}}=f \otimes 1:M \otimes_{R}R_{S} \rightarrow N \otimes_{R} R_{S}(m \otimes a/s \mapsto f(m) \otimes a/s)$と定義する.
(1)$\mathrm{Im}f \otimes R_{S} \cong \mathrm{Im}f_{R_{S}} $
(2)$\mathrm{Ker}f \otimes_{R} R_{S} = \mathrm{Ker}f_{R_{S}}$
$f_{S}:M_{S}\rightarrow N_{S}(m/s \mapsto f(m)/s)$とする.
(一般の場合が示されたため省略しました.)
おわりに
マヌケ($1$年前の自分)は見つかったようだな!!
まさか平坦加群なら,単射も全射も不要だったとは….
まぁ正しい情報に更新できてより良い記事になったのでよしとしましょう.
ちなみに付け加えると,圏論の言葉まで拡張すると$\mathrm{Im}$は完全性が必要ですが$\mathrm{Ker}$の方は左完全だけで十分だったりします.
(つまり$\mathrm{Hom}$関手については$\mathrm{Ker}$の交換可能です.)
以上,ケンけんでした.
参考文献
[1]松村英之, 可換環論, 共立出版