こんにちは!ケンけんです。
絶対に理解するHom関手第4弾で、連載は最終回になります。
今回は、Homの直和や直積の同型など雑多な性質たちをまとめていきます。
細かく節分けで扱い、最後は扱った性質を使って自由加群の場合を考えます。
それでは行ってみよう!
キーワード:$\mathrm{Hom}$関手
すごい単純化
まず、$\mathrm{Hom}$関手は、定義域を環にしているとHomは値域の加群と同型になります。
$R$を環とし, $M$を$R$加群とする.
- $\mathrm{Hom}_{R}(R,M) \cong M$.
$m \in M$を固定した作用$\mu_{m}:R \rightarrow M(r \mapsto rm)$として,$F,G$を次のように定義する.
$F:\mathrm{Hom}_{R}(R,M) \rightarrow M(f \mapsto f(1_{R}))$,
$G:M \rightarrow \mathrm{Hom}_{R}(R,M)(m \mapsto \mu_{m})$.
$F, G$が$R$線形写像としてwell-definedであることは明らかである.
従って, $G=F^{-1}$を示せば十分である.
各$f \in \mathrm{Hom}_{R}(R,M)$について, $(G \circ F)(f)=G(f(1_{R}))=\mu_{f(1_{R})}$となる.
各$r \in R$で$\mu_{f(1_{R})}(r)=rf(1_{R})=f(r)$となるため, $\mu_{f(1_{R})}=f$である.
以上から, $G \circ F=\mathrm{id}_{\mathrm{Hom}_{R}(R,M)}$である.
各$m \in M$について$(F \circ G)(m)=F(\mu_{m})\mu_{m}(1_{R})=m$となる.
従って, $G \circ F=\mathrm{id}_{M}$であり, $G=F^{-1}$である.
$\square$
定義域・値域の加群 同型での書き換え
次は、ありきたりですが()内の加群は同型を通して変えてもHom本体は同型になることです。
$R$を環とし, $L, M, N$を$R$加群とする.
$L,M$は$f:L \overset{\sim}{\rightarrow} M$により同型とする.
$(1)$ $f^{*}:\mathrm{Hom}_{R}(M,N) \rightarrow \mathrm{Hom}_{R}(L,N)$は同型写像である,
$(2)$ $f_{*}:\mathrm{Hom}_{R}(N,L) \rightarrow \mathrm{Hom}_{R}(N,M)$は同型写像である.
証明は第2回での短完全列を利用すると直接証明より簡単です。
$(1)$ 次の短完全列
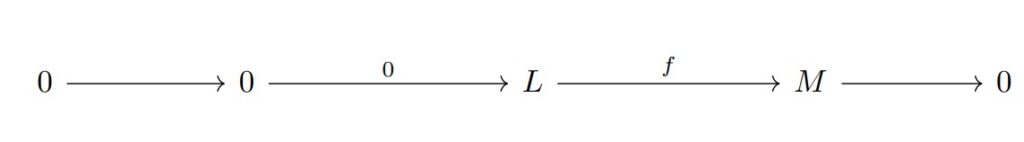
について$\mathrm{Hom}_{R}(-,N)$を取ると次の完全列が得られる.
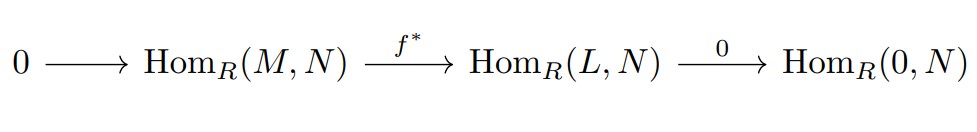
$\mathrm{Hom}_{R}(0,N)=0$より$f^{*}$は同型である.
$(2)$ 次の短完全列
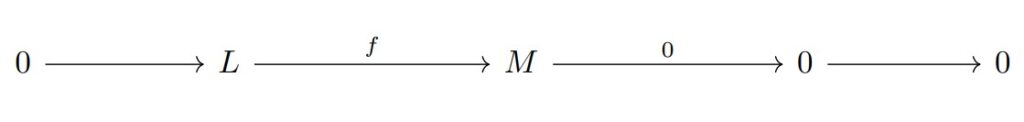
について$\mathrm{Hom}_{R}(N,-)$を取ると次の完全列が得られる.
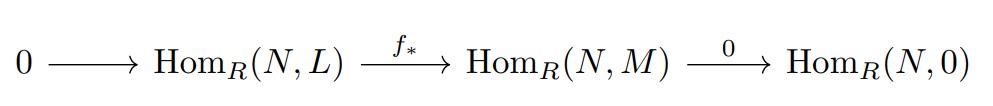
$\mathrm{Hom}_{R}(N,0)=0$より$f_{*}$は同型である.
$\square$
Hom関手 中と外の直和・直積
そして、加群の直和・直積をHomの中と外で同型を通して出し入れできることが次の主張です。
$R$を環とし, $M,M_{j}, N , N_{j}(j \in I)$を$R$加群とする.
$i_{k}:M_{k} \rightarrow \bigoplus_{j}M_{j}$を自然な単射,
$p_{k}:\Pi_{j}M_{j} \rightarrow M_{k}$を$M_{j}$への射影とする.
$(1)$ $\phi:\mathrm{Hom}_{R}(\bigoplus_{j}M_{j},N) \rightarrow \Pi_{j}\mathrm{Hom}_{R}(M_{j},N)(f \mapsto (f \circ i_{j}))$は同型写像である.
$(2)$ $\phi:\mathrm{Hom}_{R}(M,\Pi_{j}N_{j}) \rightarrow \Pi_{j}\mathrm{Hom}_{R}(M,N_{j})(f \mapsto (p_{j} \circ f))$は同型写像である.
証明が長く、それぞれで直和・直積の性質を使っているため分けて示します。
$f=f’ \in \mathrm{Hom}_{R}(\bigoplus_{j}M_{j},N)$を取ると,
各$j$について$f \circ i_{j}=f’ \circ i_{j}$より$\phi(f)=\phi(f’)$でwell-definedである.
また, $f,g \in \mathrm{Hom}_{R}(\bigoplus_{j}M_{j},N)$と$r \in R$について, 各$j$で次が成り立つ.
$(f+g) \circ i_{j}=f \circ i_{j}+g \circ i_{j}$, $(rf) \circ i_{j}=r(f \circ i_{j})$.
従って, $R$線形写像であるため全単射であることを示せば十分である.
単射について,
$f \in \mathrm{Ker}\phi$を取ると, $\phi(f)=(f \circ i_{j})=(0)$である.
従って, 各$j$について$f \circ i_{j}=0$である.
任意の$(m_{j}) \in \bigoplus_{j}M_{j}$について有限和$\sum_{j}i_{j}(m_{j})$に書けるため, 次が成り立つ.
$f((m_{j}))=\sum_{j}(f \circ i_{j})(m_{j})=0$,
以上から, $f=0$であり$\mathrm{Ker}\phi=0$で$\phi$は単射である.
全射について,
任意の$(g_{j}) \in \Pi_{j}\mathrm{Hom}_{R}(M_{j},N)$に対して$g:\bigoplus_{j}M_{j} \rightarrow N$を次で定義する.
$g((m_{j}))=\sum_{j}g_{j}(m_{j})$.
$(m_{j}) \in \bigoplus_{j}M_{j}$より$\sum_{j}g_{j}(m_{j})$が有限和である.
well-definedと$R$線形写像は成分ごとに調べることで示される.
$\phi(g)=(g \circ i_{j})=(g_{j})$より, $\phi$は全射である.
$\square$
()内の加群が直和なのは、全射となるための$g$がwell-definedになるようにするためです。
これが直積では、和$\sum_{j}g_{j}(m_{j})$が無限個(または非可算も)の和になり表現ができません。
なので、有限個を除き成分が$0$となる直和である必要があるのです。
$(1)$と同様に成分ごとに調べることでwell-definedと$R$線形写像であることが示される.
よって, $\phi$が全単射であることを示せば十分である.
単射について,
$f \in \mathrm{Ker}\phi$を取ると, 各$j$で$p_{j} \circ f=0$である.
よって, 各$m \in M$で$f(m)=(n_{j})=(0)$から$f=0$である.
従って, $\mathrm{Ker}\phi=(0)$で$\phi$は単射である.
全射について,
任意の$(g_{i}) \in \Pi_{j}\mathrm{Hom}_{R}(M,N_{j})$を取り, $g:M \rightarrow \Pi_{j}N_{j}$を次のように定義する.
$g(m)=(g_{j}(m))$
各成分ごとに調べることでwell-definedと$R$線形写像であることが示される.
$(p_{j} \circ g)(m)=g_{j}(m)$より, $\phi(g)=(p_{j} \circ g)=(g_{j})$である.
従って, $\phi$は全射である.
$\square$
結果 自由加群の場合
さて最後は、今回示した同型を利用して
$$自由加群Fによる\mathrm{Hom}_{R}(F,-)は完全である.$$
ことを示します。
$R$を環とし, $F$を自由$R$加群とする.($F \cong R^{I}=\bigoplus_{i \in I}R,I$は添字集合)
また, 次の$R$加群の短完全列を取る.
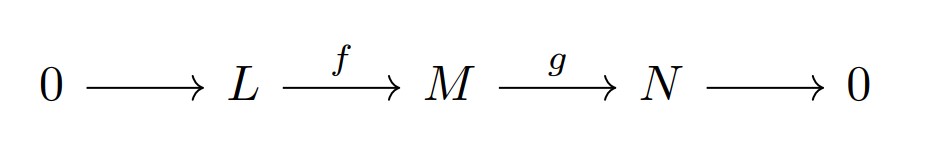
次は完全列である.
$$0 \rightarrow \mathrm{Hom}_{R}(F,L) \overset{f_{*}}{\rightarrow} \mathrm{Hom}_{R}(F,M) \overset{g_{*}}{\rightarrow} \mathrm{Hom}_{R}(F,N) \rightarrow 0$$
$\mathrm{Hom}_{R}(-,F)$は左完全である.
従って, $g_{*}$が全射であることを示せば十分である.
ここで, $g$について$\Pi_{j}g:\Pi_{j}M \rightarrow \Pi_{j}N((m_{j}) \mapsto (g(m_{j})))$により次の図式が得られる.
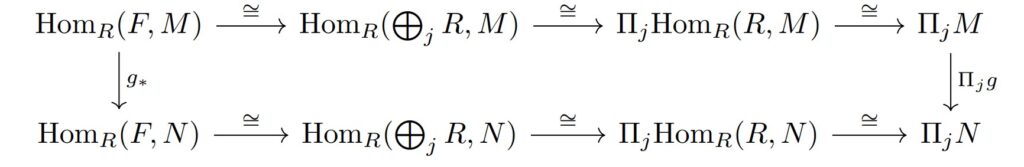
これは, 命題1-3で構成した同型写像を利用することで可換図式であることがわかる.
$g$が全射より, $\Pi_{j}g$も全射であるため$g_{*}$も全射である.
$\square$
このように、$\mathrm{Hom}_{R}(\bigcirc,-)$の$\bigcirc$に入れる加群(今回は自由加群)によって左完全から完全関手になる性質があります。
当然、$\mathrm{Hom}_{R}(-,\bigcirc)$を完全関手にする加群もあります。
おわりに
と言うわけで、「絶対に理解するHom関手」は今回で終了です。
このような一つの対象だけでシリーズを作るのは初めてでしたが、範囲が狭いからこそ語るべき情報・追加するといい情報の精査が整理しながらするのが楽しかったです。
特に今回最後の命題(自由加群による完全性)は、「自由加群$\Rightarrow$射影加群」の証明方法の一つだと言えます。一般的には、自由加群の基底の性質を使います。
と言っても、実際はその3は半分以上が圏論なのでHom関手単体の話は1,2,4の3本だけという。
(正直その3は書き直しを検討中)
次の話を書くとしたら次の3つがあります。
- 完全列と鎖複体(ホモロジー代数)
- テンソル積(Hom関手と随伴関係がある)
- 射影加群(今回の自由加群の例を一般化した加群)
落ち着いたらこれらのどれかに手を出したいです。
以上、ケンけんでした。