こんにちは!ケンけんです。
素朴集合論第二弾「同値類と商集合」のはじまりです。
記念すべき第一回は集合を分類して分ける「類別」を扱います。
キーワード:類別
導入 類別
「集合は部分集合を持つ」ことは、さすがにもう当たり前になっているでしょう。
(空集合$\emptyset$や自分自身が部分集合となる 参照1, 参照2)
それでは味気ないので集合$X$に対して、$\emptyset, X$以外の部分集合$Y$を取ります。
そうすると、$Y$について補集合$Y^{c}$が取れましたね。
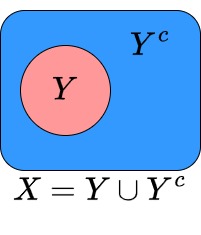
図:$X$と部分集合$Y$
このとき、全体$X$は$Y \cup Y^{c}$だと言えますね。
このような全体集合を部分集合の和集合で表現することが目的です。
ただ、部分集合分けるだけではあまり分類できていると言いにくいです。
まずは、分類の意義から考えます。
例えば、動物の分類は特定の特徴から「~目~科~属」と言うように決めています。
そして、分類の別れ方は大体が「~を持っている。~を持っていない。」です。
一度分類用の本を見るとわかりますが、本当に「~がついているか」や「~を持っているか」でフローチャートのように見分けていきます。
(理科で有名な脊椎動物は脊椎を持つ動物であり持たない方は他の脊索動物になります。)
この「~を持つ。~を持たない。」は二値論理となっていますね。
また、二値論理で分類しているため、一つの種が別々の科に属したりすることはありません。
そして、すべての目・科・属などを合わせて考えるともとの「生物」全体になります。
従って、分類は次の3点を行っています。
- 二値論理で特定の集団に分ける。($\in$と$\notin$)
- 分けられた対象は他の集団に入らない,(共通部分がない)
- すべての分類を考えるともとの対象の全体である.(和集合が全体)
先ほどの、述語$P(x)$「部分集合の元である」について$P(x) \vee \neg P(x)$は恒真命題です。
$X$は$Y$か$Y^{c}$に分けられ、共通部分は空集合、そして$X=Y \cup Y^{c}$となります。
また、$P(x) \wedge \neg P(x)$は恒偽命題となります。($Y \cap Y^{c}=\emptyset$を指す)
つまり、先ほどの部分集合と補集合の分け方は分類の性質を満たすことになります。
部分集合での和集合表示で、一般的な分類と同様の性質を持つ場合に「類別」と呼びます。
(一般的な分類は、二値論理から構成されたものなのである種こちらが定義)
また各部分集合のことを「類」と呼ぶ場合もあります。
導入 代表系
集合レベルの話の後は、元レベルの話です。
次に、集合$X$と$Y \subset X$に対して類別$X=Y \cup Y^{c}$の元を考えます。
$y \in Y$と$y’ \in Y^{c}$を取ると、$\{y,y’\}$は$Y$と$Y^{c}$の元をひとつずつ持つ集合です。
そして、これだけで類別$Y \cup Y^{c}$の分け方は2通りであることがわかります。
このような集合を「代表系」と呼びます。
これではあまりピンとこないので、有理整数全体の集合$\mathbb{Z}$で類別を考えます。
整数は、偶数と奇数に分割できます。
偶数全体の集合を$Z=2\mathbb{Z}$とすると、その奇数全体の集合は$Z^{c}$です。
従って、$\mathbb{Z}=Z \cup Z^{c}$で類別になっています。
これについて、先ほど代表系と呼んだ集合を取ろうとすると次のようにいろいろあります。
$$\{1,2\}, \{0,1\}, \{2,3\}, \ldots$$
つまり代表系は、取り方がいくらでもありますが類別がわかるのならどうとってもいいのです。
(数字の列を与えられて空いている数字を予想する遊びのイメージ)
さらに差が出るのは、$3$の倍数とあまり$1,2$の場合の3に分ける場合です。
$Z=3\mathbb{Z},Z_{1}=3\mathbb{Z}+1,Z_{2}=3\mathbb{Z}+2$とすると$\mathbb{Z}=Z \cup Z_{1} \cap Z_{2}$です。
また、$Z,Z_{1},Z_{2}$はそれぞれ共通部分を持たないので類別になります。
この代表系は$\{0,1,2\}$とすると一目で$3$で割ったあまりで分けられているとわかります。
代表系をうまく使って考える対象を減らすことが、類別を考える理由の一つです。
定義 類別と代表系
それでは定義していきます。
$X$:集合 $I$:添え字集合(非可算も可)
$\mathfrak{X}=\{X_{i} \in 2^{X}|(i \in I) \wedge (i \neq j \Rightarrow X_{i} \cap X_{j}= \emptyset)\}$
$X=\bigcup_{i \in I}X_{i}$と書くことを$\mathfrak{X}$により類別する($\rm{classification}$)と言う.
$\{x_{i}|\forall i \in I(x_{i} \in X_{i}) \}$:類別$X=\bigcup_{i \in I}X_{i}$の代表系($\rm{system \; of \; representatives}$)
代表系の元は代表元と呼ぶ.
導入の例は有限個の部分集合でしたが、分割するための部分集合は非可算個でも問題ありません。
おわりに
類別と代表系だけだと特に話すことがないので今回は導入と定義だけになってしまいました。
これから、類別の仕方によって代表系が意味を持つようになります。
それはある一定の条件の下で部分集合の元を同じとする方法です。
そのための意味として「同値類」を次回取り扱います。
以上、ケンけんでした。