RING-L-14：整数環で見る次元と素イデアル　イデアルの対応

$R$を環とし, $\sum_{R}$を$R$のイデアル全体の集合とする.

$I \in \sum_{R}$を取る.

$X=\{J \in \sum_{R}|I \subset J \}$とおく.

このとき, $X$と$\sum_{R/I}$は次の写像により包含関係を保つ一対一対応する.

$\Phi:X \rightarrow \sum_{R/I}(J \mapsto \pi(J))$

$\Psi:\sum_{R/I} \rightarrow X(J’ \mapsto \pi^{-1}(J’))$

（$\pi:R \rightarrow R/I$は自然な準同型）

$R$を環とし, $\mathrm{Spec}R$を$R$の素イデアル全体の集合とする.

$I \subset R$をイデアルとして$\mathcal{V}(I)$を次のように定義する.

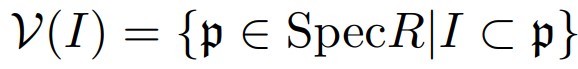
このとき, $\mathcal{V}(I)$と$\mathrm{Spec}(R/I)$は次の写像により包含関係を保つ一対一対応する.

$\Phi:\mathcal{V}(I) \rightarrow \mathrm{Spec}(R/I)(\mathfrak{p} \mapsto \pi(\mathfrak{p}))$

$\Psi:\mathrm{Spec}(R/I) \rightarrow \mathcal{V}(I)(\mathfrak{p’} \mapsto \pi^{-1}(\mathfrak{p’}))$

（$\pi:R \rightarrow R/I$は自然な準同型）

命題1よりイデアルの対応は明らかである.

従って, 素イデアルである確認をすれば十分である.

$\Phi$について

各$\mathfrak{p} \in \mathcal{V}(I)$に対して, $\overline{xy} \in \pi(\mathfrak{p})$を取る.

このとき, $xy-p =i \in I \subset \mathfrak{p}(p \in \mathfrak{p})$と書ける.

よって$xy=p+i \in \mathfrak{p}$から$x \in \mathfrak{p}$または$y \in \mathfrak{p}$となる.

従って, $\overline{x} \in \pi(\mathfrak{p})$または$\overline{y} \in \pi(\mathfrak{p})$で$\pi(\mathfrak{p}) \in \mathrm{Spec}(R/I)$である.

$\Psi$について

素イデアルの逆像は素イデアルである.

従って, 各$\mathfrak{p’} \in \mathrm{Spec}(R/I)$について$\pi^{-1}(\mathfrak{p’}) \in \mathrm{Spec}R$である.

よって, $\pi^{-1}(\mathfrak{p’}) \in \mathcal{V}(I)$である.

$\square$

$R$を環とし, $\mathrm{Max}R$を$R$の極大イデアル全体の集合とする.

$I \subset R$をイデアルとして$\mathcal{M}(I)=\mathrm{Max}R \cap \mathcal{V}(I)$を取る.

このとき, $\mathcal{M}(I)$と$\mathrm{Spec}(R/I)$は次の写像により包含関係を保つ一対一対応する.

$\Phi:\mathcal{M}(I) \rightarrow \mathrm{Max}(R/I)(\mathfrak{m} \mapsto \pi(\mathfrak{m}))$

$\Psi:\mathrm{Max}(R/I) \rightarrow \mathcal{M}(I)(\mathfrak{m’} \mapsto \pi^{-1}(\mathfrak{m’}))$

（$\pi:R \rightarrow R/I$は自然な準同型）