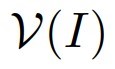こんにちは!ケンけんです。前回は、内点と触点を取り上げ元レベルの「近さ」情報を考えてました。さらには、内部と開集合の判定も取り上げました。
今回は、第一弾の最後として「閉集合」と触点の関係を取り上げます。
キーワード:閉集合
導入 何が閉か?
今回取り扱う「閉集合」には「閉」が使われておりこれを理解すれば特徴がよくわかります。
そうすると、まずは何の「開閉」なのかをはっきりさせないといけません。
現段階で使える道具は次の通りです。
- 位相と開集合
- 近傍・基本近傍系
- 元の列の極限
- 内点と触点
今回は、極限による説明をします。
集合の元の列(点列)が収束するかは、一般にはわかりませんが収束する場合はその元が決まります。
これを考えるために登場するのが、前回定義した「触点」と「閉包」です。
閉包にも「閉」という字が使われていますが、これも極限の収束先が閉じていることを意味します。
実際に確かめてみましょう。
位相空間$(X,\mathcal{O}(X))$の元の列$(a_{n})_{n \in \mathbb{N}}$が$a \in X$に収束するとは、次の条件を満たすことでした。(詳しくはPST-4参照)
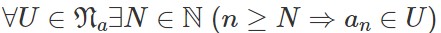
第1の目標は「$A \subset X$の元からなる収束する列$(a_{n})$の収束先$a$は$\overline{A}$の元」です。
すると次のように$a \in \overline{A}$が考えられます。
- 任意の$U \in \mathfrak{N}_{a}$に対して$N \in \mathbb{N}$項目以降は$a_{n} \in U$である,
- 各$n$で$a_{n} \in A$より, $n \geq N$ならば$a_{n} \in U \cap A$である,
- $U \cap A \neq \emptyset$より, $a \in \overline{A}$である.
つまり、「閉包を取る」操作は集合の元とその元の列の収束先をすべて含むような集合と言えます。
と言うことは、$\overline{A}$の元からなる収束する列$(a_{n})$は$\overline{\overline{A}}$の元だと言えます。
では、「集合の閉包を取る」操作を2回するとどうなるでしょう。
第2目標は「$\overline{\overline{A}}=\overline{A}$」です。
「$\overline{A} \subset \overline{\overline{A}}$」は明らかなので逆を調べる必要があります。
各$x \in \overline{\overline{A}}$を取ると, 任意の開近傍$U \in \mathfrak{N}_{x}$について$U \cap \overline{A} \neq \emptyset$となる.
このとき, ある$y \in U \cap \overline{A}$が存在し$y \in \mathfrak{N}_{y}$である.
$y \in \overline{A}$より, $y$の近傍$U$について$U \cap A \neq \emptyset$である.
従って, 任意の$x$の開近傍$U$については$U \cap A \neq \emptyset$である.
よって, 任意の$x$の近傍$U$についても同様に$U \cap A \neq \emptyset$である.
以上から, $x \in \overline{A}$であり$\overline{\overline{A}} \subset \overline{A}$である.
$\square$
開近傍で$\neq$を調べることで、それらを含む一般の近傍も$\neq$であることを示せました。
従って、「集合の閉包」の元からなる列の収束先ははみ出すことなく「集合の閉包」の元になります。
つまり、元の部分集合$A$について$\overline{A}=A$なら次のことが言えます。
$$Aの元の収束する列(a_{n})の極限を取る操作で閉じている$$
これが、閉集合の「閉」の意味と認識すればいいでしょう。
定義 閉集合
それでは、定義なのですが今回は閉包の条件を基本にして他と同値だと示していきます。
$(X,\mathcal{O}(X))$:位相空間 $A \subset X$
$A$は閉集合($\rm{closed \; set}$)である $\overset{def}{\iff} \overline{A}=A$
(*$\overline{A}=\mathrm{Cl}(A)$は$A$の閉包)
そして次が同値な定義です。(大抵の本では次の$\rm{(2)}$を定義としています。)
$(X,\mathcal{O}(X))$を位相空間とし, $A \subset X$を取る.
このとき以下は互いに同値である.
$\rm{(1)}$ $A$は閉集合である,
$\rm{(2)}$ $A^{c}=X \backslash A$は開集合である.
添え字が煩雑になるので、内部$A^{\circ}$を$\mathrm{Int}A$と表記します。
$\rm{(1)} \Rightarrow \rm{(2)}$について
$A^{c}$が開集合であるとは、内部と一致することを示せば十分である.
$\mathrm{Int}(A^{c}) \subset A^{c}$は定義から明らかより, 逆の包含を示せば十分である.
任意の$x \in A^{c}$を取ると, $x \notin A=\overline{A}$よりある$U \in \mathfrak{N}_{x}$で$U \cap A = \emptyset$が成り立つ.
これより, $U \subset A^{c}$である.
従って, $x \in \mathrm{Int}(A^{c})$であり$A^{c} \subset \mathrm{Int}(A^{c})$である.
$\rm{(2)} \Rightarrow \rm{(1)}$について
$A$が閉集合であるとは, $\overline{A}=A$を示せば十分である.
$\overline{A} \subset A$を示せば十分である.
$A^{c}$は開集合より, $\mathrm{Int}(A^{c})=A^{c}$である.
任意の$x \in A^{c}$を取ると, $U \subset A^{c}$を満たす$U \in \mathfrak{N}_{x}$が存在する.
従って, $U \cap A=\emptyset$となるため$x \notin \overline{A}$である.
以上から, $\overline{A} \cap A^{c}=\emptyset$なので$\overline{A} \subset A$である.
$\square$
うまく補集合を利用することで双方向の証明ができました。
閉集合であることを最後に「$\overline{A} \cap A^{c}=\emptyset$」を使いました。
これは、包含関係$\overline{A} \subset A$の対偶として次を示しています。

特定の近傍$U$で$A$との共通部分が空集合となり、触点ではないため$x \notin \overline{A}$です。
また、$\rm{(2)}$を利用して位相の定義を利用した次の定義も存在します。
$X$:集合 $\mathcal{A}(X) \subset 2^{X}$ $I$:添字集合 $i \in I$
- $\emptyset, X \in \mathcal{A}(X)$
- 任意個の$X_{i} \in \mathcal{A}(X)$に対し, $\cap_{i \in I}X_{i} \in \mathcal{A}(X)$,
- $Y,Z \in \mathcal{A}(X) \Rightarrow Y \cup Z \in \mathcal{A}(X)$
$\mathcal{A}(X)$を閉集合系と呼び, その元を閉集合と呼ぶ.
このとき, 次が位相となる.
$\mathcal{O}(X)=\{A \in 2^{X}|\exists U \in \mathcal{A}(X) \; s.t. \; A=U^{c}\}$
補集合を取る操作は2回繰り返すと元に戻るので、位相と閉集合系のつながりは全単射になります。
6-2の条件から、「閉集合系を先に定義して」位相を「その補集合たちで構成すること」で位相から出発した手順を再び使うことができます。
次につながる話
位相空間論の始めの目標「極限」について議論が終わりました。
一つの位相空間を見る手段はある程度準備できたので、次に目指すは2つの位相空間の比較です。
その中心となる道具は「連続写像」です。
これは、高校数学での連続関数をただの集合に一般化したものです。
(もちろん実数全体の集合を定義域にすると、関数に戻ります。)
連続写像は、関数では途切れず繋がっているグラフをイメージするでしょうが実際には途切れて見える関数でも連続な関数はあったはずです。($x=0$だけ別の値を取っているものなど。)
連続性は、定義に極限を使っていました。
これは、グラフ上の点と関数が「近い」ことを意味します。
一般の位相空間は、像と値域の元の近さを近傍により比較し「連続性」を考えます。
近傍が使えるなら開集合も利用します。
集合の同型が「等濃である」ことならば、位相の同型は「位相が同じ」ことだと言えます。
それを調べる手段として連続写像を利用するのです。
おわりに
位相空間論は、連続写像やのちのコンパクト・連結・分離公理などが注目されがちです。
先の知識が重要な道具なら、これまでに取り扱った道具は新しく構成するために必要な土台です。
近傍系・基本近傍系による位相の構成は、新しく位相を入れたり位相を整える場面で役立ちます。
位相の基礎を見直すきっかけになっていればうれしいです。
以上、ケンけんでした。