こんにちは!ケンけんです。前回で、第一弾の極限について扱いました。
今回は、集合レベルの話から元に注目することで開集合の性質を見ていきます。
キーワード:内点・触点
導入
1.内点
位相は、近傍系の公理(PST-3,3′参照)では位相を次の同じ部分集合族として構成しています。
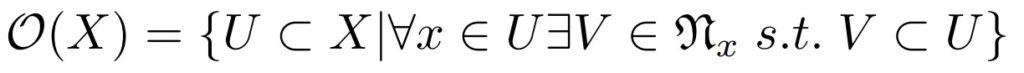
今回は、この共通する位相の条件に注目します。
この位相では、開集合の元はすべて述語部分の条件を満たすことになります。つまり、「述語部分を満たす元の集合」として開集合を見てもよさそうです。
そこで、上の位相において部分集合$Y \subset X$を取り次のようなさらに部分集合を考えます。
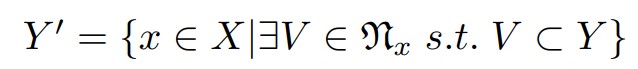
これは、位相の定義から開集合になっていますね。(述語部分が全く同じ)
$Y’$の元は「内点」、$Y’$自身を「内部」と呼ばれます。
これでちょうど$Y$が自分自身の元で近傍になっていることがわかります。
$$x \in Y \Rightarrow x \in Y’ \subset Y$$
(要確認:$Y’$の元は$X$の元ですが、実際は$Y$の元からしか取れません。ヒントは近傍)
もちろん一般の位相では、$Y’$が開集合とは限らないのでいつも言えるわけではありません。
しかし、私たちは開集合からさらに覆うモノとして近傍を定義してきました。
つまり、先の$Y’$のような部分集合を考える意味はありそうです。
2.触点
ここからは、新しい考えです。
位相は、「元の間で近さ」を考える道具として導入してきました。
そうすると、2つの元が接触するかかが考えられます。
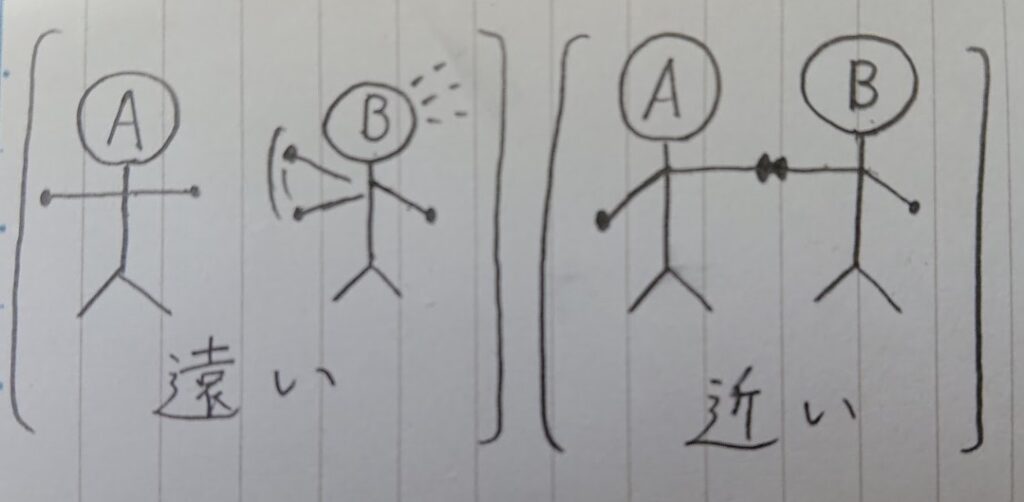
図:元の接触(二人が手を繋げるか)
集合の元に手はなく、元は集合での点のようなモノなので、何かで置き換える必要があります。
ここに、集合と近さの情報を持つ開集合を使います。
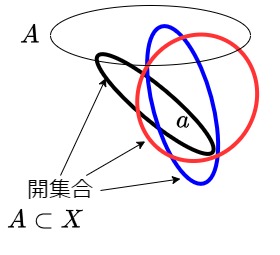
図:部分集合$A$と元$a$の開集合
集合と元の接触を次のように定義します。
- 基準となる部分集合$A$と適当な元$a$を一つとる,
- $a$を含むすべての開集合が$A$と共通部分を持つ,
- 元$a$は$A$と接触している.
$a$を含む適当な部分集合ではなく開集合なのは、接触する基準を近さで決めたいからです。
では、「すべての」開集合と共通部分を持つ必要はあるでしょうか。
ここで、極限の「すべての近傍」と同様に考えます。
握手する例では気になりませんが、集合と元では開集合と共通部分を持たない場合があり得ます。
そこで、Aさん(集合)とBさん(元)について次のように考えます。
$$AさんはBさんと握手できる \Rightarrow Aさんは常に握手できるほどBさんに近い$$
そこで、接触していることを「どの近さ(開集合)でも重なる」ことだと言い換えます。
極限と同様に、「すべての開近傍を考えること」は「すべての近傍を考えること」でした。
従って、集合$A$に元$a$が接触していることを次のように表現します。
$$\forall V \in \mathfrak{N}_{a} \;s.t. \; V \cap A \neq \emptyset$$
この接触する条件を満たす元を「触点」と呼びます。
集合と(ここまで積み上げた意味で)接触している元だから触点です。
定義 内点・触点
それでは定義します。
$(X,\mathcal{O}(X))$:位相空間 $A \subset X$ $x \in X$
$x$は$A$の内点 $\overset{def}{\iff} \exists V \in \mathfrak{N}_{x} \; s.t. \; V \subset A$
$\mathrm{Int}A=\{x \in X|x:Aの内点\}$を$A$の内部と呼ぶ.
($A^{\circ}$とも書く.)
$x$は$A$の触点 $\overset{def}{\iff} \forall V \in \mathfrak{N}_{x} \; s.t. \; V \cap A \neq \emptyset$
$\overline{A}=\{x \in X|x:Aの触点\}$を$A$の閉包と呼ぶ.
($\mathrm{Cl}(A)$とも書く.)
内部と開集合
ここからは、内部と開集合の関係を見ていきます。
先の内点の定義を考えるとすぐにわかりますが、位相空間$(X,\mathcal{O}(X))$の部分集合$A$が開集合の場合は$A^{\circ}=A$を満たします。
(定義部分の近傍を開集合$A$自身で取れるため.)
つまりは次が成り立っています。
$$A \in \mathcal{O}(X) \Rightarrow A^{\circ}=A$$
こうなると逆の矢印はどうなのかが気になりますね。
これが同値なら開集合と内部の特徴づけや、選んだ部分集合が開集合かの判定に使えるからです。
そして、実際に成り立ちます。
$(X,\mathcal{O}(X))$を位相空間とし, $A \subset X$と$x \in X$を取る.
このとき, 次が成り立つ.
$$A \in \mathcal{O}(X) \iff A^{\circ}=A$$
$\Leftarrow$のみ示す.
各$x \in A=A^{\circ}$を取ると, ある近傍$V_{x} \in \mathfrak{N}_{x}$で$x \in V_{x} \subset A$が成り立つ.
近傍$V_{x}$について$x \in O_{x} \subset V_{x}$とする開集合$O_{x} \in \mathcal{O}(X)$が存在する.
$O=\bigcup_{x \in A}O_{x}$を取ると, これは開集合である.
集合として$O=A$となるため, $A$は開集合である.
$\square$
これで、開集合単体を調べる手段ができました。
実はこれまで一般の位相での開集合は判定できませんでした。
なぜなら、開集合は「位相$\mathcal{O}(X)$の条件を満たす部分集合」としか説明がないからです。
近傍系や基本近傍系を使った場合、位相は固定されますが今度は近傍系が必要です。
今回の内部を使った方法は、近傍系による位相の場合は定義の述語を調べているだけです。
その手法が、一般の位相でも利用できるところがポイントですね。
おわりに
今回は、位相空間論でかなり重要な2つの特殊な元を扱いました。本来は後4つほど特殊な元がありますが、今回の2つほどではないためそれぞれ個別で取り扱いたいと思います。
(あまり使わない用語の動機付けは難しい…)
そして、今回考察部分で触れなかった触点は次回の「閉集合」とセットで取り扱います。
解析学だと開集合よりこっちの方が重要なケースが多いです。
以上、ケンけんでした。