こんにちは!今回は、高校数学Ⅱで登場する二項定理とその係数を可換環上で考えるとどうなるのか、その応用をまとめたので記事に書いていきます。
それでは行ってみよう!
キーワード:二項定理
この記事では、環はすべて単位的可換環とします。
二項定理
まずは、基本の定理を可換環上でも成り立つことを確認しましょう。
二項係数$_{n}C_{i}$は、元の数を表すものとして使用します。
つまり、$x+x+x=3x=_{3}C_{1}x$といった風に使います。
(高校数学での組み合わせと同じです。)
二項定理は次のような主張でした。
$R$を環とし, $a,b \in R$を取る.
このとき, 次が成り立つ.
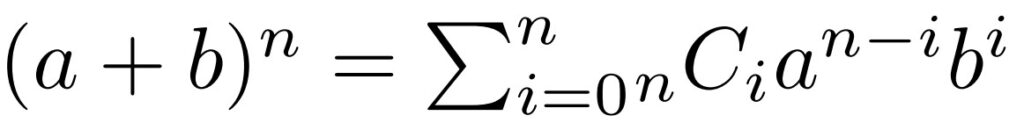
証明自体は、$n$に関する帰納法で実数などと同様に証明できます。
実数の四則演算しか利用しないため環の加法と乗法だけで十分だからです。
この性質から、可換環のべき零元全体がイデアルになることを示せます。
$R$を環とし, $N(R)=\{a \in R|\exists n \in \mathbb{Z}_{\geq 0} \; s.t. \; a^n=0\}$を取る.
このとき, $N(R)$は$R$のイデアルでありべき零根基($\rm{nil \; radical}$)と呼ぶ.
$0 \in N(R)$より$N(R) \neq \emptyset$となる.
$a,b \in N(R)$を取ると, ある$m,n \in \mathbb{Z}_{\geq 0}$によって$a^m=b^n=0$となる.
従って, 次のように$a+b \in N(R)$であることがわかる.
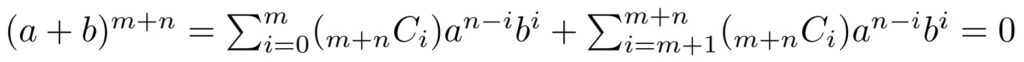
また$r \in R$について$(rx)^m=r^mx^m=0$より$rx \in N(R)$となる.
以上から, $N(R)$は$R$のイデアルである.
$\square$
可換環である必要性は、先の表記をするためには$ab=ba$ができる必要があるからです。
仮に非可換の場合、$ab \neq ba$ならば次のように表記できなくなります。

単元とべき零元
ここからが、今回の動機の問題です。
以前の記事で単位元とべき零元の差が単元となることを示していましたが、もっと一般化できます。
それが次の主張です。
$R$を環とし, $u$を$R$の単元, $a$はべき零元とする.
このとき, $(u+a)$は$R$の単元である.
$u,a$について, 定義からある$b \in R,n \in \mathbb{Z}_{\geq 0}$が存在し$ub=1,a^n=0$となる.
$u=(u+a)-a$によって, べき零元$(-ab)=1-(u+a)b$を得る.
従って, $0=(-ab)^n=\sum_{i=0}^n(_{n}C_{i})(-(u+a)b)^i$.
$1=\sum_{i=1}^n(_{n}C_{i})(-1)^{i+1}((u+a)b)^i$から, $(u+a)^{-1}=(\sum_{i=1}^n(_{n}C_{i})(-1)^{i+1}(u+a)^{i-1}b^i)$.
以上から, $(u+a)$は$R$の単元である.
$\square$
この命題はよく参考書でも現れるものです。
では、べき零元を少し弱めて零因子にするとどうでしょう。
これは、$\mathbb{Z}$で反例があります。(整数環便利すぎる。)
$\mathbb{Z}/6\mathbb{Z}$について,
$\rm{(1)}$:零因子は$\overline{0},\overline{2},\overline{3},\overline{4}$
$\rm{(2)}$:単元は$\overline{1},\overline{5}$
このとき, $\overline{5}+\overline{3}=\overline{2}$で零因子より単元ではない.
また、ここで課題として元を取り換えた次のものがあります。
$R$を環とし, $u$を単元, $a$を冪等元とする.
このとき, $u+a$は単元や冪等元になるのか?
先ほどの反例では、$\overline{3},\overline{4}$が冪等元になっています。
このとき、$\overline{5}+\overline{3}=\overline{2}$で単元でも冪等元でもありません。
また、$\overline{5}+\overline{4}=\overline{3}$は冪等元になっています。
従って、これも大した特徴はないでしょう。
おわりに
今回は、可換環での二項定理の利用として単元・べき零元の特徴を表す問題を取り上げました。
あまり環論では表に出てこない冪等元ですが、なかなか面白い性質ないです。
一応剰余環の冪等元があるようですが、自分が考えている剰余環の零因子やべき零元に近い話なので模索を続けたいです。
以上、ケンけんでした。