こんにちは!ケンけんです。PST-3では、近傍系による位相の構成を取り扱いましたが、実はもっと簡単に似たようなことができます。それが、基本近傍系です。
今回は、その定義と位相の構成まで見ていきます。
キーワード:基本近傍系
定義とイメージ 基本近傍系
今回は近傍を絞った概念なので、定義から見ていきます。
$(X, \mathfrak{O}(X))$を位相空間として, $x \in X$に対する近傍系を$\mathfrak{N}_{x}$と書く.
$\mathcal{N}(x) \subset \mathfrak{N}_{x}$を取る.
$\mathcal{N}(x)$は基本近傍系$\overset{def}{\iff} (x \in U \in \mathcal{O}(X) \Rightarrow \exists N \in \mathcal{N}(x)(N \subset U))$
これは近傍の中からさらに絞った集合族です。
定義からわかりますが、$x$を含む開近傍全体からなる近傍系の部分集合は基本近傍系です。
($N=U$とすればいい。)
また、元の近傍系もすべての開近傍を含んでいるため明らかです。
では、どうすればそうではないのかを見ていきます。
$X=\{a,b,c\}$と位相$\mathcal{O}(X)=\{\emptyset, \{a\}, \{a,b\}, X\}$とします。
このとき、$\mathfrak{N}_{a}=\{\{a\},\{a,b\}, \{a,c\}, X\}$となります。
このとき、$\mathcal{N}(a)=\{\{a,b\}, \{a,c\}, X\}$として見ます。
そうすると、$U \subset \{a\}$とする$U$が$\mathcal{N}(a)$に存在しません。
従って、これは近傍系の一部ですが基本近傍系ではありません。
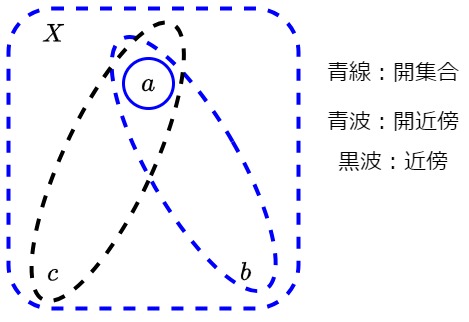
図:反例の図
つまり、位相が全順序になっている場合は$a$を含む最小(極小でも可)の開集合は最低限含めないと基本近傍系とならないことがわかります。
ここまで、きれいな位相はなかなかありませんが近傍の定義を考えると、どの開近傍も含めておくことで無難に構成できると言えます。
そして、これに適当な近傍を加えても定義は崩れません。
従って、近傍系と異なり構成方法はいくらでもあると言えます。
それこそ、位相が先ほどの一列に並ぶ例では$\{a\}$のみ持つ部分集合でも問題ないわけです。
近傍系だとすべての条件を満たすものでしたが、今回は一つ存在すればいいため最小の開集合だけで定義を満たすからです。
満たす性質と構成する道具
それでは近傍系と同様に、いくつかの満たす性質たちを見ていきます。
$(X,\mathcal{O}(X))$を位相空間とし, $x \in X$の基本近傍系を$\mathcal{N}(x)$と書く.
このとき, 次の性質を満たす.
$\rm{(1)}$ $\mathcal{N}(x) \neq \emptyset$,
$\rm{(2)}$ $N \in \mathcal{N}(x) \Rightarrow x \in N$,
$\rm{(3)}$ $\forall N_{1}, \forall N_{2} \in \mathcal{N}(x) \exists N_{3} \in \mathcal{N}(x) \; s.t. \; N_{3} \subset N_{1} \cap N_{2}$,
$\rm{(4)}$ $\forall N_{1} \in \mathcal{N}(x) \exists N_{2} \in \mathcal{N}(x) \forall y \in N_{2} \exists N_{3} \in \mathcal{N}(y) \;s.t. \; N_{3} \subset N_{1}$.
$\rm{(4)}$だけは実は普通の書き方と変えています。
大抵の書籍で、「十分小さな」と言う無定義用語を利用しているためです。
日本語説明すると次のようになっています。
- 任意の$N_{1} \in \mathcal{N}(x)$に対して,
- 「任意の$y \in N_{2}$について$N_{3} \subset N_{1}$とする$N_{3} \in \mathcal{N}(y)$が存在する.」
- このような$N_{2} \in \mathcal{N}(x)$をひとつは選べる.
この$N_{2}$に「十分小さな」という文言がついています。
$\rm{(2)}$は近傍の定義から明らかなので$\rm{(1),(3),(4)}$を示します。
$\rm{(1)}$ 開集合$X$に対して任意の$x$を含む部分集合$N$で$N \subset X$である.
従って, $N \in \mathcal{N}(x) \neq \emptyset$である.
$\rm{(3)}$ $N_{1}, N_{2} \in \mathcal{N}(x)$を取る.
このとき, $x \in U_{1} \subset N_{1}, x \in U_{2} \subset N_{2}$とする開集合$U_{1},U_{2} $が存在する.
従って, $x \in U_{1} \cap U_{2} \subset N_{1} \cap N_{2}$となる.
$U_{1} \cap U_{2} \in \mathcal{O}(X)$より, $x \in N_{3} \subset U_{1} \cap U_{2}$とする$N_{3} \in \mathcal{N}(x)$が存在する.
以上から, $N_{3} \subset U_{1} \cap U_{2} \subset N_{1} \cap N_{2}$が得られる.
$\rm{(4)}$ 任意の$N_{1} \in \mathcal{N}(x)$を取る.
$N_{1}$は$x$の近傍より, $x \in U_{1} \subset N_{1}$とする開集合$U_{1}$が存在する.
この$U_{1}$に対して, $N_{2} \subset U_{1}$を満たす$N_{2} \in \mathcal{N}(x)$が存在する.
任意の$y \in N_{2}$に対し, $ y \in U_{1}$より$N_{3} \subset U_{1}$を満たす$N_{3} \in \mathcal{N}(y)$が存在する.
以上から, $N_{3} \subset N_{1}$となる.
$\square$
位相を作る
さて、ここまでは前座です。
今から、先ほどの3つの性質を持つ集合族で位相を作れることを示すのですが、これが中々大変です。
$X$を集合とする.
各$x \in X$について$\mathcal{N}(x)$をPST-3′-2の4つの主張を満たす部分集合の族とする.
このとき, 次の集合族は$\mathcal{N}(x)$を基本近傍系とする$X$の位相となる.
$\mathcal{O}(X)=\{U \subset X|\forall y \in U \exists N \in \mathcal{N}(y) \; s.t. \; N \subset U\}$
主張自体は、近傍系から位相を作ることと同じです。
$X,\emptyset$について
各$y \in X$について$N \subset X$を満たす$N \in \mathcal{N}(y)$が存在する.
また, $\emptyset$の場合は,次の主張の仮定部分が偽となる.
$\forall y \in \emptyset\exists N \in \mathcal{N}(y) N \subset \emptyset \Rightarrow \emptyset \in \mathcal{O}(X)$
従って, $X, \emptyset \in \mathcal{O}(X)$である.
和集合について
$U_{\lambda} \in \mathcal{O}(X)$を取り, $y \in \cup _{\lambda \in \Lambda}U_{\lambda}$を取る.
ある$\lambda$で$y \in U_{\lambda} \in \mathcal{O}(X)$である.
従って, $N \subset U_{\lambda}$とする$N \in \mathcal{N}(y)$が存在する.
よって, $y \in N \subset \cup _{\lambda \in \Lambda}U_{\lambda}$から$\cup _{\lambda \in \Lambda}U_{\lambda} \mathcal{O}(X)$である.
共通部分について
$U,V\in \mathcal{O}(X)$を取り, $y \in U \cap V$を取る.
このとき, $y N_{1} \subset U,y \in N_{2} \subset V$を満たす$N_{1},N_{2} \in \mathcal{N}(y)$が存在する.
従って, $y \in N_{1} \cap N_{2} \subset U \cap V$である.
PST-3′-2 $\rm{(3)}$から, $N_{3} \subset N_{1} \cap N_{2}$とする$N_{3} \in \mathcal{N}(y)$が存在する.
よって, $y \in N_{3} \subset U \cap V$から$U \cap V \in \mathcal{O}(X)$である.
以上から, $\mathcal{O}(X)$は位相である.
$N \in \mathcal{N}(x)$が$x$の近傍であることを示す.
$P=\{y \in X|\exists N’ \in \mathcal{N}(y) \; s.t. \; N’ \subset N\}$を取ると$x \in P$が成り立つ.
$y \in P$とする$y$について, $y \in N’ \subset N$とする$N’ \in \mathcal{N}(y)$が存在する.
従って, $P \subset N$となるため$P$が開集合であることを示せば十分である.
$N’$に対して, PST-3′-2 $\rm{(4)}$を用いると,次を満たすある$N_{1} \in \mathcal{N}(y)$が存在する.
「各$z \in N_{1}$について$N_{2} \subset N’$とする$N_{2} \in \mathcal{N}(z)$が存在する.」
$z \in N_{2} \subset N’ \subset N$より, $z \in P$である.
$z$は任意だったので, $N_{1} \subset P$である.
以上から, $P \in \mathcal{O}(X)$である.
最後に基本近傍系であることは, 位相の定義部分から明らかである.
$\square$
おわりに
と言うわけで、少し制限をかけた近傍でも位相を同じ形で構成できることがわかりました。
なぜこんなものを導入する必要があったのかは、距離空間での$\epsilon$近傍や位相群の近傍系の考えに現れ整えられるからです。
どちらもいずれ記事にします。
以上、ケンけんでした。