こんにちは!ケンけんです。
前回は、近傍系の持つ性質から逆に位相を作ることを見ました。
今回は、第一弾の主題「極限」を取り扱います。
これをイメージできれば、ほかの極限も同様に見えるようになります。
キーワード:位相空間の極限
導入
まずは、極限の直感的な復習から始めます。何度も登場した次のグラフを考えます。
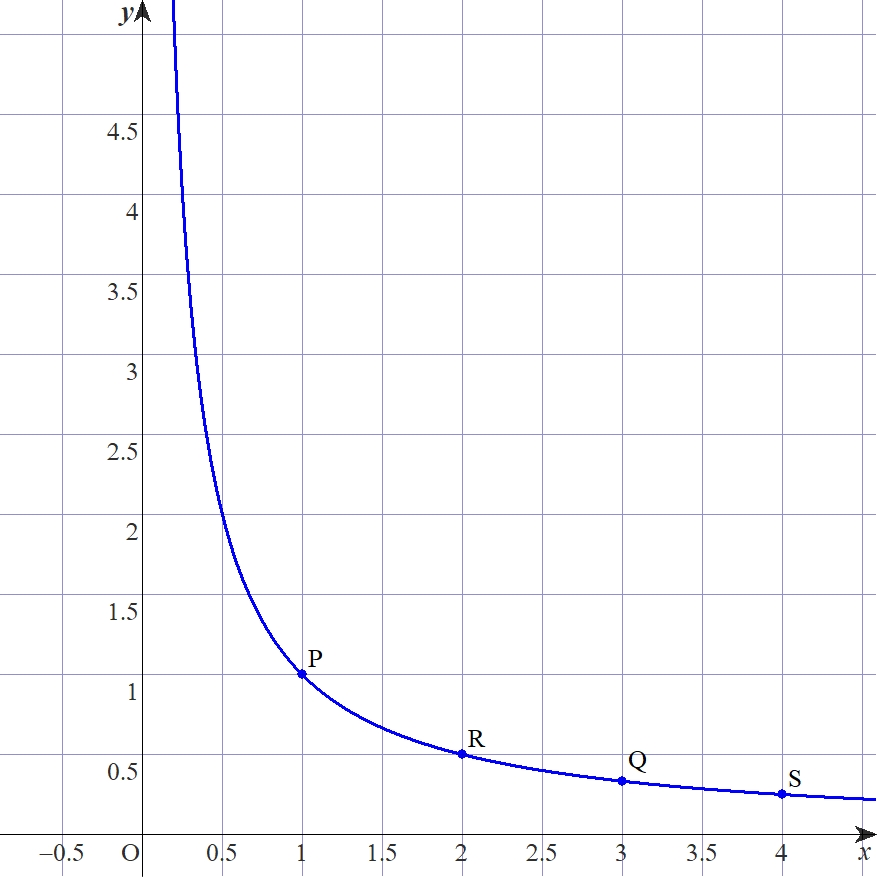
図:$f(x)=\frac{1}{x}$のグラフ
数列$\{\frac{1}{n}\}$は$x$が自然数の部分です。このとき、$n \rightarrow \infty$を考えると極限値$0$に収束するとしていました。そして、その説明にこの文言があったことでしょう。
$$限りなく近づく$$
大学の非数学科向けテキストの微分積分学の本でもこの文言は見られます。
よく間違いだとやり玉に挙げられる文言ですが、実は間違ったことは言っていません。
ただ「近づく」ことをしっかり定義していないから、厳密ではないだけなのです。
今私たちは、「近さ」として位相を持ち出し考えてきました。
数列が極限値に収束することを位相の言葉に置き換えてみましょう。
まず、位相を導入した例から近さの見方を振り返ります。
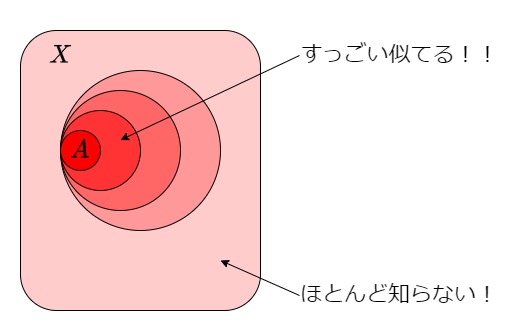
図:近さのイメージ図(再掲)
これは、第一回の考察部分で挙げた近さのイメージです。開集合(大丸)の重なりが多いほどAさんに似ていると見ていました。この例では、Aさん自身だけの集合も開集合(人間関係)に含めていたため、Aさんに最も似ている人はAさん自身しかいません。
しかし、この開集合を抜いて考えるとどうでしょう。そうなると、Aさん以外に最も近い人が存在する可能性が出てきます。上の図の最も小さい円(開集合)の中は、Aさん以外にもいるかもしれません。
まず、この学校の生徒と言うモデルでAさんを必ず含むような人間関係だけに単純化します。
つまりは、どのような開集合を取ってきても上の図のような人間関係の集団ができます。
全校生徒を一列に並べて、数列のように$\{a_{n}\}$と見てみます。(有限の列ですが)
このとき、数列が「Aさんに収束する」は「Aさんに限りなく近づく」ことでした。
最も近いのは、一番小さい人間関係の中にいる生徒たちです。
「近づく」と言う意味から、列の後ろの方の生徒が全員最小のAさんの人間関係に属していると考えるのが妥当でしょう。
(そっくりさんが途中から最後まで並んでるのは恐怖ですが)
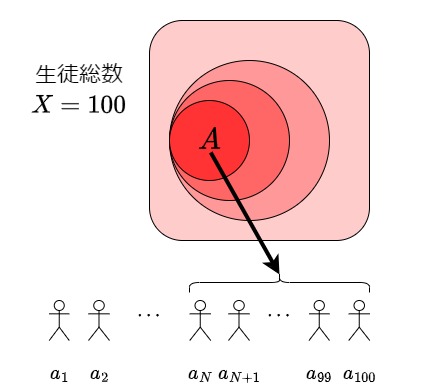
図:生徒の列がAさんに近づくイメージ
では、途中で最小の人間関係に含まれている生徒が混じっている場合どうすればいいでしょう?
「近づく」とは最終的にAさんそっくりになることなので途中の例外は無視し、最小の人間関係に属する生徒が最後まで続く部分があるかを見ればいいわけです。
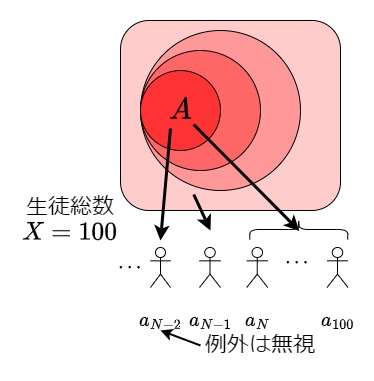
図:途中に例外がいるケース
以上から、このケースでの生徒の列$\{a_{n}\}$がAさんに収束するとは次のように書けそうです。
$$最小の開集合Uに対し,「n \geq N \Rightarrow a_{n} \in U」が真となるNが存在する.$$
しかし、実際には開集合が常に包含関係を持つ上の例ではありません。
(つまり全順序とは限らない。それこそ第一回のケースが該当する。)
そこで、「最も小さい開集合に属する」の言い換えを考えます。
先の例では、「Aさんが属するすべての開集合に属する」と言い換えることができます。
近傍は開集合を含むものより、「すべてのAさんの近傍に属する」に言いかえができます。
以上から、「限りなく近づく」は次の3種類の言い方ができます。
- Aさんを含む最も小さい開集合に属する
- Aさんが属するすべての開集合に属する
- すべてのAさんの近傍に属する
「2.から1.への言いかえ」と「2.と3.の間で言いかえ」は常に成り立ちますが、「2.から1.」は先ほどのようにAさんを含む開集合で最小のものがない場合は成り立ちません。
以上から、命題としては次のようになります。
$$3. \iff 2. \Leftarrow 1.$$
以上から、近傍系として書きやすい3.を定義として採用するのがよさそうです。
ここまでのイメージは有限集合でした。
しかし、別に無限集合と無限に続く列$\{a_{n}\}$にしても同じようになります。
$$任意のxの近傍Uに対し,「n \geq N \Rightarrow a_{n} \in U」が成り立つN \in \mathbb{N}が存在する.$$
($\{a_{n}\}$が$x$に収束する場合)
始めのケースでも有限集合の性質を使わなかったので、そのまま拡張できました。
位相空間の極限
それでは、極限と収束を定義します。
$(X,\mathcal{O}(X))$を位相空間とし, $\{a_{n}\}_{n \in \mathbb{N}}$を添え字づけられた$X$の部分集合とする.
$a \in X$を取り, $\mathfrak{N}_{a}$をその近傍系とする.
$\rm{*}:$ $\forall U \in \mathfrak{N}_{a} \exists N \in \mathbb{N}$ $(n \geq N \Rightarrow a_{n} \in U)$
$\{a_{n}\}$は$a$に収束する($\rm{convergence}$) $\overset{def}{\iff} \{a_{n}\}$は$\rm{*}$を満たす.
$\underset{n \rightarrow \infty}{\lim}a_{n}=a$と記述する.(位相空間の極限($\rm{limit}$))
数列の極限との比較
ここからは、少し数列の極限と見比べていきます。
実数列$\{a_{n}\}_{n \in \mathbb{N}}$が$a$に収束するとは次が成り立つことです。
$$\forall \epsilon > 0 \exists N \in \mathbb{N}(n \geq N \Rightarrow |a_{n}-a| <\epsilon)$$
これが、位相の考えに従っているなら先の定義と同じ表示ができるはずですね。
まずは、演算(引き算や絶対値)を条件文から解消してみます。
$U(a,\epsilon)=\{y \in \mathbb{R}||y-a |<\epsilon\}$とおくと、$a_{n} \in U(a, \epsilon)$と置き換えることができます。
実は、この$U(a,\epsilon)$は$a$の$\epsilon$近傍と呼ばれます。
では位相はどうなっている?となります。
ここで使用するのが、この記事で考えた「基本近傍系から位相を構成する」手法です。
$\mathbb{R}$上の各$a$で$\mathfrak{N}_{a}=\{U(a, \epsilon)|\epsilon >0\}$と定義することで$a$の基本近傍系となります。
(証明には、実数の四則演算を使います。)
従って、次のように書き換えることができます。
$$\forall U=U(a,\epsilon) \in \mathcal{N}(a) \exists N \in \mathbb{N}(n \geq N \Rightarrow a_{n} \in U)$$
同じように記述できましたね。基本は、今回の定義通りなのです。
(数列の場合に復元できるので、今回の定義が問題ないこともわかるでしょう。)
これで作られる位相によって今までの座標平面上の近さなども議論することができます。
実際には、上の実数の位相と一般の位相の間にはさらに距離位相が存在します。
$$実数の位相 \Rightarrow 距離位相 \Rightarrow 一般の位相$$
あくまで一般の位相空間を考えているため距離位相と実数の位相は今は見ません。
おわりに
結構は早めに、目標としていた極限と収束に到達できました。
今回で、極限とその収束について新しい見方が増やせたと思います。
(今回の定義を知らない場合、位相群のコーシー列で苦しむことになります。経験談)
しかし、今後距離位相などを考えるならまだ言葉が不十分です。
開集合や近傍と言った集合レベルの話から元レベルの話に注目することです。
次回は、位相空間の「特別な元たち」を取り上げます。
以上、ケンけんでした。
参考文献
筆者が見た中で、一般の位相での収束(今回の定義)を書いている数少ない本
[1] 森田紀一, 位相空間論, 岩波書店(1981)