こんにちは!ケンけんです。前回は、人間関係の回り「傍観者」を含む集まりとして近傍を導入しました。今回は、近傍が持つ性質を使って逆に位相を構成しようと言う内容です。なので今回は証明が主体となります。考察パートでは、作った位相がどのようになっているか見ます。
キーワード:近傍系による位相
近傍系が持つ性質
開集合を覆うという点から近傍を考えていましたが、これは位相($\mathcal{O}(X)$)が満たしている性質をある程度は近傍も持っていると言えます。それが次の4つの性質です。
$(X,\mathcal{O}(X))$を位相空間とし, $\mathfrak{N}_{x}$を$x \in X$の近傍系とする.
このとき, 次が成り立つ.
$\rm{(1)}$ $U \in \mathfrak{N}_{x} \Rightarrow x \in U$,
$\rm{(2)}$ $U,V \in \mathfrak{N}_{x} \Rightarrow U \cap V \in \mathfrak{N}_{x}$,
$\rm{(3)}$ $(U \in \mathfrak{N}_{x}) \wedge (U \subset V \subset X) \Rightarrow V \in \mathfrak{N}_{x}$,
$\rm{(4)}$ $U \in \mathfrak{N}_{x} \Rightarrow \overset{\circ}{U}=\{y \in U|U \in \mathfrak{N}_{y}\} \in \mathfrak{N}_{x}$.
$\rm{(1)}$は近傍の定義から明らかですね。なので、$\rm{(2)}$以降を示します。
$\rm{(2)}$ $U,V \in \mathfrak{N}_{x}$を取る.
定義から, $x \in U_{1} \subset U,x \in U_{2} \subset V$を満たす開集合$U_{1},U_{2}$が存在する.
$U_{1} \cap U_{2}$は開集合であり, $x \in U_{1} \cap U_{2} \subset U \cap V$となる.
従って, $U \cap V \in \mathfrak{N}_{x}$である.
$\rm{(3)}$ $U \in \mathfrak{N}_{x}$と$V \subset X$を取り, $U \subset V \subset X$を仮定する.
$x \in U_{1} \subset U \subset V$とする開集合$U_{1}$が存在するため, $V$は$x$の近傍である.
$\rm{(4)}$ $U \in \mathfrak{N}_{x}$を取ると, $x \in V \subset U$を満たす開集合$V$が存在する.
$y \in V \subset U$から, $V$の元は$\overset{\cdot}{U}$の元の条件を満たし$x \in V \subset \overset{\cdot}{U}$である.
以上から, $\overset{\cdot}{U} \in \mathfrak{N}_{x}$である.
$\square$
示したところで、一つずつ何が起こっていたのか見ていきます。
$\rm{(1)}$は定義から明らかで、覆うのだから当然の性質です。
$\rm{(2)}$は、位相の定義「有限個の開集合の共通部分が開集合」から導かれるものです。
人間関係(位相)を覆う2つの傍観者含めた集団(近傍)で共通部分を取ったら、人間関係の重複部分を覆うようになるのは当然です。

図:2つの近傍の共通部分
$\rm{(3)}$は、近傍を含む部分集合がそのまま近傍としての延長と見れることを示しています。
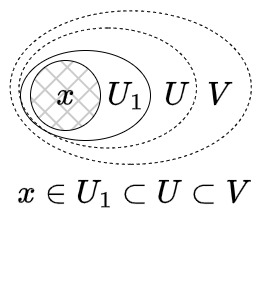
図:近傍の延長($U_{1}$が開集合, $U$が$x$の近傍)
そして、一見難しそうな$\rm{(4)}$も証明からわかるように開集合の適当な元すべての近傍になっていることを示しています。

図:$x$の近傍としての開集合$U_{1}$と$y \in U_{1}$の近傍としての$U$
近傍系による位相
さて、今回の主題は導入の4つを近傍の公理として位相を新しく作ることです。
$X$を集合として, $x \in X$を取る.
$\mathfrak{N}_{x}$をPST-3-1の4つの主張を満たす$X$の部分集合の族とする.
このとき, 次の集合族$\mathcal{O}(X)$は$X$の位相である.
$\mathcal{O}(X)=\{U \in 2^{X}|\forall y \in U \exists V \in \mathfrak{N}_{y} \;s.t. \; V \subset U\}$
1. $X$と$\emptyset$について
$x \in X$に対し, すべての$U \in \mathfrak{N}_{x}$で$x \in U \subset X$より$X \in \mathcal{O}(X)$である.
$\emptyset$は元を持たないため, 次の命題の仮定部分が成立しない.
$(\forall x \in \emptyset \exists U \in \mathfrak{N}_{x}(U \subset \emptyset \Rightarrow \emptyset \in \mathcal{O}(X)))$
(この記事の考えを利用)
従って, 強制的に真で$\emptyset \in \mathcal{O}(X)$である.
2. 和集合について
$\Lambda$を添字集合として$\{O_{\lambda}\}_{\lambda \in \Lambda}$を$\mathcal{O}(X)$の族とする.
$x \in \cup_{\lambda}O_{\lambda}$を取ると, ある$\lambda$について$x \in O_{\lambda}$である.
ある$V \in \mathfrak{N}_{x}$が存在し$x \in V \subset O_{\lambda}$である.
従って, $x \in V \subset O_{\lambda} \subset \cup_{\lambda}O_{\lambda}$が成り立つ.
以上から, $\cup_{\lambda}O_{\lambda} \in \mathcal{O}(X)$である.
3. 共通部分について
$O_{1},O_{2} \in \mathcal{O}(X)$に対して, $x \in O_{1} \cap O_{2}$を取る.
ある$V_{1},V_{2} \in \mathfrak{N}_{x}$が存在し$x \in V_{1} \subset O_{1}, \; x \in V_{2} \subset O_{2}$が成り立つ.
PST-3-1 $\rm{(2)}$より, $V_{1} \cap V_{2} \in \mathfrak{N}_{x}$である.
よって, $x \in V_{1} \cap V_{2} \subset O_{1} \cap O_{2}$である.
以上から, $O_{1} \cap O_{2} \in \mathcal{O}(X)$である.
従って, $\mathcal{O}(X)$は$X$の位相である.
$\square$
近傍は直接関係のない傍観者も含めた集団でしたが、その中に人間関係を含むことが条件としてありました。近傍から位相(人間関係)作れましたが、近傍の公理はそれだけではありません。
なんと各$x$について、$\mathfrak{N}_{x}$は定理で証明した$\mathcal{O}(X)$から構成される近傍系$\mathfrak{N}_{x}$と一致します。
$X$を集合として, $x \in X$を取る.
$\mathfrak{N}_{x}$をPST-3-1の4つの主張を満たす$X$の部分集合とする.
次の集合族$\mathcal{O}(X)$を$X$の位相とする.
$\mathcal{O}(X)=\{U \in 2^{X}|\forall y \in U \exists V \in \mathfrak{N}_{y} \;s.t. \; V \subset U\}$
- このとき, $x$の近傍系$\mathfrak{N}_{x}’$は$\mathfrak{N}_{x}$と同じ族である.
$U \in \mathfrak{N}_{x}$を取り, $U’=\{y \in X|U \in \mathfrak{N}_{y}\}$を定義する.
各$y \in U’$について, $y \in U \in \mathfrak{N}_{y}$より$U’ \subset U$である.
$U’ \in \mathcal{O}(X)$を示せば, $U \in \mathfrak{N}_{x}’$が示される.
$\overset{\circ}{U}=\{z \in U|U \in \mathfrak{N}_{z}\}$を取る.
$N \in \mathfrak{N}_{y}$より, PST-3-1$\rm{(4)}$から$\overset{\circ}{U} \in \mathfrak{N}_{y}$である.
$\overset{\circ}{U} \subset U’$であるため, PST-3-1$\rm{(3)}$から$U’ \in \mathfrak{N}_{y}$である.
また, 各$y$について$\overset{\circ}{U} \in \mathfrak{N}_{y}$で$\overset{\circ}{U} \subset U’$より$U’ \in \mathcal{O}(X)$である.
従って, $\mathfrak{N}_{x} \subset \mathfrak{N}_{x}’$である.
逆に, $U \in \mathfrak{N}_{x}’$を取る.
このとき, ある$U’ \in \mathcal{O}(X)$により$x \in U’ \subset U$を満たす.
各$y \in U’$について, ある$V \in \mathfrak{N}_{y}$が存在し$V \subset U’$である.
PST-3-1$\rm{(3)}$より, $U’ \in \mathfrak{N}_{y}$である.
従って, $x$についても$x \in U’ \in \mathfrak{N}_{x}$である.
$U’ \subset U$から, 再度PST-3-1$\rm{(3)}$を利用し$U \in \mathfrak{N}_{x}$である.
以上から, $\mathfrak{N}_{x}’ \subset \mathfrak{N}_{x}$である.
$\square$
この事実から、近傍系を最低限3-1の条件を満たすようにして自分たちが作りたいように組み立てることができるのです。これが効果を発揮するのは代数学に位相を持ち込んだ時です。詳細はここでは語りませんが、特別な近傍系を先に設定することで、位相空間となる群・環・体に整った近さを定義でき、「完備化」を考える際に有用となります。
おわりに
今回は、近傍系と位相の関係を見ていきました。近傍は位相から定義されたものでしたが、逆に位相を定義することもできる重要な道具だったわけです。必要な場面は、具体的対象を扱うときに近傍系をうまく作りたい場合までありませんが使えるようになると位相の見方がグッと変わると思います。試しに、有限集合などで考えてみてください。
次回は、第一弾の主題「極限」を取り扱います。
以上、ケンけんでした。