こんにちは!ケンけんです。前回は、人間関係という視点から位相の定義に対して動機づけを得ました。今回は、前回の考察で触れた「近さ」にさらに踏み込んだ「位相の近傍」を扱います。
キーワード:位相の近傍
導入
実は前回の考察で考えた近さの議論からほとんど答えが出ています。
再度、前回考えた人間関係の図から思い返します。
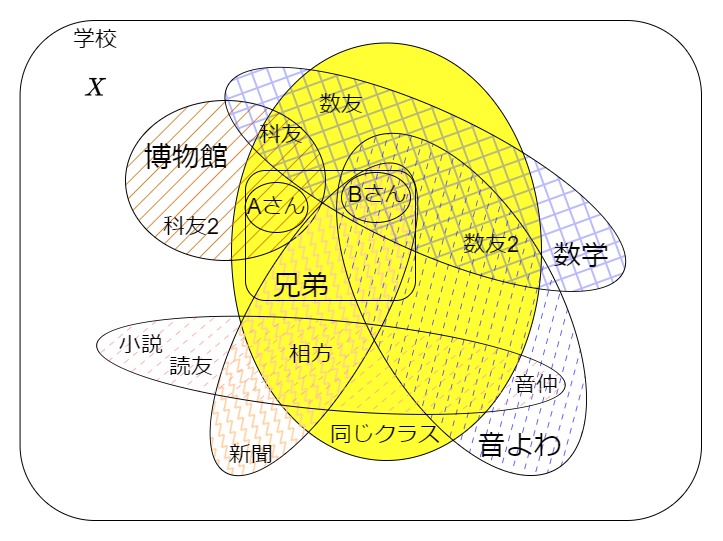
図:AさんBさん、その周りの人間関係の図
詳しい設定は前回をご覧ください。このとき、Aさんの近さは、「Aさんと同じ関係で何度も重なる人ほど本人に近い!」と考えていました。上の例では、Aさんの博物館仲間「科友さん、科友2さん」ではAさんと同じクラスである科友さんの方がより近い関係だと言えます。逆に、Bさんの新聞委員の「相方さん」が属する小説の情報共有の関係がある「読友さん」はAさんとほとんど関係がなく、遠い関係だと言えます。このように、同じグループ(集団)に属すかで関係の近さを表していました。
では、グループの周りには全く人はいないでしょうか?そんなことはなくグループ外の無関係な人たちもいますね。Aさんの博物館グループで考えます。このとき、Aさんと「数友さん」やBさんの新聞委員の「相方さん」は博物館のグループで関係はなく同じクラスの関係です。しかし、Aさんと同じクラスのため博物館グループがAさんのクラスで集まっているところを見かけることもあるでしょう。そう考えると、この二人も博物館グループとは直接関係がなくとも「見たことがある」と言った間接的に関係を持っていると言えます。いわゆる「傍観者」と言うことです。
つまり次の図のように、博物館グループの関係者の周りをさらに傍観者の集団でおおわれます。
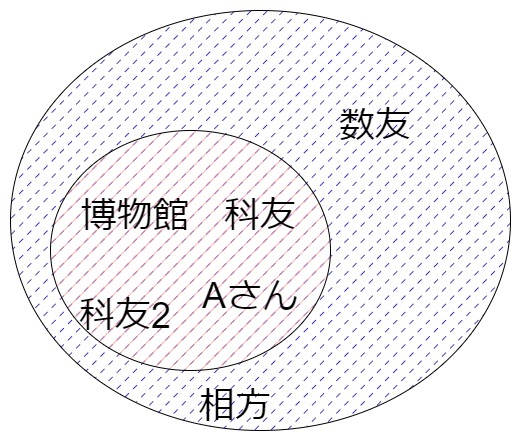
図:博物館グループとその周り
この傍観者の取り方はAさんが所属するクラスの人ならいくらでも考えられます。初めの図だと
- 数友2さん・相方さん・Bさん
- Bさん・数友さん・数友2さん
- 誰も傍観者として選ばない
と言ったように傍観者の取り方があり得ます。これらは、すべて傍観者を含めた博物館グループの関係を表す集団です。
これが、Aさんの近傍と呼ばれる集合の一種です。特に、誰も傍観者として選ばない場合近傍は開集合そのものになります。
ただし、あくまで傍観者で直接関係がないためグループを覆う集合は「開集合」とは限りません。なぜなら、
- 数友さんと相方さんは博物館グループと直接関係はない
- 科友2さんと相方さんはAさんかBさんが少なからず関係を持つ同じグループの人ではない
なので、上の場合での位相の定義
$$\mathcal{O}(X)=\{Y \in 2^{X}|P(Y) \vee Q(Y)\}$$
- $P(Y)$:$Y$はAさんとBさんを含む人間関係で決まる集合
- $Q(Y)$:$Y$はAさんBさんを含まないが関係を持つ人を含む人間関係で決まる集合
を満たしていません。従って、$\{Aさん, 科友, 科友2, 数友, 相方\}$は開集合になりません。
これが、まさしく近傍であって開集合ではない例です。
また、AさんBさんの人間関係ではAさんとBさんの自分自身と言う関係によって開集合を取っています。なので、AさんとBさんの近傍は自分以外の生徒を適当に取ってもすべて近傍になります。つまり次のようなものです。
$$\{Aさん\}\subset M(Aさんの近傍), \{Bさん\}\subset N(Bさんの近傍)$$
と言うわけで整理です。Aさんの近傍は
- Aさんを必ず含む,
- 何かしらの人間関係(開集合)とグループの外から見ている傍観者も含めた集団,
- 開集合になるとは限らない.
と言う性質を持っています。これをもとに一般化して定義します。
定義 位相の近傍
それでは、定義しましょう。
$(X,\mathcal{O}(X))$:位相空間 $V \subset X$ $x \in V$
$U$は$x$の近傍($\rm{neighborhood}$) $\overset{def}{\iff} \exists U \in \mathcal{O}(X) s.t. \; x \in U \subset V$
$\mathfrak{N}_{x}=\{V \in 2^{X}|Vはxの近傍\}$:$x$の近傍系($\rm{system \; of \; neighborhoods \; of }$ $x$)
集合として一般化しても近傍はベン図としては同じものを表しています。
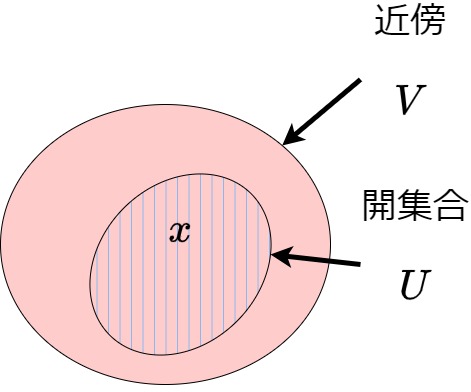
図:一般の位相空間での元$x$の近傍
導入でもふれたように、近傍の定義自体は開集合も満たしています。この場合の近傍は、特別に「開近傍」と呼びます。
近傍は開近傍だけで十分?
位相空間$(X,\mathcal{O}(X))$について元$x$の近傍を考えると定義からすべて$x$を元として持つ開集合を含んでいました。そうすると、$x$の近傍系$\mathfrak{N}_{x}$には必ず$x$を元として持つ開集合をすべて持っています。
つまり、「集合の元である関係$\in $」については次のことが言えます。
$$「開近傍の元である」ならば「すべての近傍の元である」$$
この事実から、書籍によっては開近傍だけを近傍と呼ぶものもあります。普通に位相空間論を展開するだけなら、この「集合の元である関係$\in $」しか必要ないからです。この差は、現代の書籍でも普通の近傍を考えたり開近傍だけだったりとまちまちです。
現状としては、まだまだ位相の性質を知らないためはっきりは言えません。
伝えられるのは次の2点です。
- 普通に位相空間を考えるだけなら開近傍だけで十分
- 普通の近傍があった方が楽なケースも存在する
1点目は、開近傍の情報からわかりました。2点目は次回取り扱います。
おわりに
「位相の近傍」と強調しましたが「元を含む」と言う情報だけなら開近傍を考えれば十分でした。これで、は近傍の強みが全然見えてきません。今回は、あくまで概念としての存在と正当性のみに絞ったのでこのような形になります。しかし、開集合ぽい集合という情報に着目した別の側面が存在します。これによって元の位相を整頓することができます。
次回は、近傍と近傍系の万能ツール「近傍による新しい位相の構成」を取り扱います。
以上、ケンけんでした。