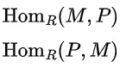こんにちはケンけんです。前回は、ずっと言語化されなかった「数えられる」ことを可算として定義し、等濃によって可算か否かを分けることができるようになりました。今回は、当初目標としていた「ベルンシュタインの定理」を取り扱います。
キーワード:ベルンシュタインの定理
まず相手を知る
今回は、主張を先に考えてそのあと考察していきます。
$U$:普遍集合 $\emptyset \neq X,Y \subset U$
$\exists f:X \rightarrow Y,\exists g:Y \rightarrow X \; s.t. f,g:単射 \Rightarrow X \sim Y$.
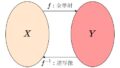
$X$と$Y$の間にある単射の情報だけで全単射を構成できると言う主張です。以前単射から値域を制限することで全単射となることは見ましたが、今回は逆方向にも単射が存在します。
非常に長いので証明は格納します。
$f:X \rightarrow Y, g:Y \rightarrow X$を単射として次のような記号を決める.
$y \in Y$に対して, $y=f(x)$とする$x \in X$が存在するとき$y > x$とする.
$x \in X$に対して, $x=g(y)$とする$y \in Y$が存在するとき$x \succ y$とする.
$X,Y$の部分集合として次のものを取る.
$X_{\infty}=\{x \in X|x \succ y_{1} > x_{1} \succ y_{2} >x_{2} \succ \cdots \}$,
$X_{X}=\{x \in X|x=x_{1} \succ y_{1} > \cdots \succ y_{n-1} >x_{n}, x_{n} \notin g(Y) \}$,
$X_{Y}=\{x \in X|x \succ y_{1} >x_{1} \cdots > x_{n-1} \succ y_{n}, y_{n} \notin f(X) \}$,
$Y_{\infty}=\{y \in Y|y >x_{1} \succ y_{1} > x_{2} \succ y_{2} > \cdots \}$,
$Y_{X}=\{y \in Y|y >x_{1} \succ y_{1} > \cdots \succ y_{n-1} > x_{n}, x_{n} \notin g(Y)\}$,
$Y_{Y}=\{y \in Y|y=y_{1} >x_{1} \succ \cdots >x_{n-1} \succ y_{n}, y_{n} \notin f(X)\}$.
$X_{\infty},X_{X},X_{Y}$は互いに共通部分を持たず, $X=X_{\infty} \cup X_{X} \cup X_{Y}$である.
同様に$Y_{\infty},Y_{X},Y_{Y}$は互いに共通部分を持たず, $Y=Y_{\infty} \cup Y_{X} \cup Y_{Y}$である.
像集合について$f(X_{\infty})=Y_{\infty},f(X_{X})=Y_{X},g(Y_{Y})=X_{Y}$が成り立つ.
$f,g$は単射より, $X_{\infty},X_{X},Y_{Y}$に定義域をそれぞれ制限しても単射である.
単射は値域を像集合に置き換えることで全単射となる.
従って, $f_{1}:X_{\infty} \rightarrow Y_{\infty}, f_{2}:X_{X} \rightarrow Y_{X},g’:Y_{Y} \rightarrow X_{Y}$は全単射である.
$X_{\infty}$と$X_{X}$の包含関係から$f’:X_{\infty} \cup X_{X} \rightarrow Y_{\infty}\cup Y_{X}$としても全単射である.
今,写像$h:X \rightarrow Y$を次のように定義する.
$$\begin{equation} h(x)= \begin{cases} f'(x) & \text{($x \in X_{\infty} \cup X_{X}$)} \\ g’^{-1}(x) & \text{($x \in X_{Y}$)} \end{cases} \end{equation}$$
$x,y \in X$を取り$x=y$を仮定する.
このとき, $x=y \in X_{\infty}\cup X_{X}$または$x=y \in X_{Y}$のいずれか一方が成立する.
$x=y \in X_{\infty}\cup X_{X}$のとき, $h(x)=f'(x)=f'(y)=h(x)$である.
$x=y \in X_{Y}$のときも同様に, $h(x)=g’^{-1}(x)=g’^{-1}(y)=h(x)$である.
従って, $h$は$\rm{well \; defined}$である.
単射性について$x,y \in X$に対して$h(x)=h(y)$を仮定する.
$(Y_{\infty} \cup Y_{X}) \cap Y_{Y} =\emptyset$より$h(x),h(y)$は同じ像集合の元である.
従って, $x, y$も$X_{\infty} \cup X_{X}$または$X_{Y}$のいずれか一方だけに入る.
このとき,$h(x)=h(y)$は$f’$または$g’^{-1}$の一方で表される.
$x,y \in X_{\infty} \cup X_{X}$のとき, $f'(x)=h(x)=h(y)=f'(x)$で,$f’$の単射性から$x=y$である.
$x,y \in X_{y}$のとき, $g’^{-1}(x)=h(x)=h(y)=g'{-1}^(x)$で,$g’^{-1}$の単射性から$x=y$である.
よって, 「$h(x)=h(y) \Rightarrow x=y$」から$h$は単射である.
全射性について, 任意の$y \in Y$を取ると$y \in Y_{\infty} \cup Y_{X}$または$y \in Y_{X}$のいずれかである.
$y \in Y_{\infty} \cup Y_{X}$のとき, $f’$の全射性からある$x \in X_{\infty} \cup X_{X} $により$y=f'(x)=h(x)$である.
$y \in Y_{X}$のとき, $g’^{-1}$の単射性よりある$x \in X_{Y}$によって$y=g’^{-1}(x)=h(x)$である.
従って, $y \in h(X)$より$Y \subset h(X)$である.
逆の包含は明らかより$h(X)=Y$となるため$h$は全射である.
以上より, $h$は全単射であり$X \sim Y$である.
$\square$
考察
実直に書くと非常に長い証明でした。流れとしては、次の3つになっています。
- 部分集合を構成して全単射になる制限写像を作る.
- 写像$h:X\rightarrow Y$を1.で作った全単射を組み合わせて作る.
- $h$が全単射であることを確認する.
1.での6つの部分集合の構成は$X$の場合は、下の図のような分け方になっています。
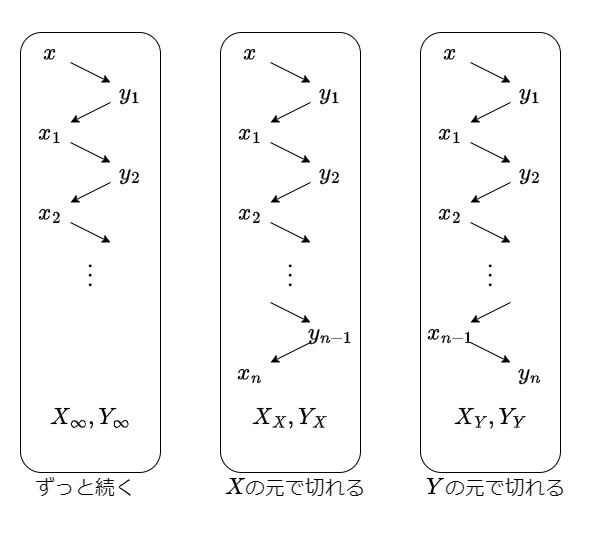
図:$X_{\infty},X_{X},X_{Y}$の分割
$Y$の場合は、スタートの$x$は$y$に置き換わって同じ図になります。この3種類の部分集合は共通部分を持たない上和集合を取ることで元の$X$に復元できます。そうすると、3つの部分集合一つごとに全単射を作ってそれを一緒に考えると全単射になりそうです。
そうして構成した全単射が、$f’:X_{\infty} \cup X_{X} \rightarrow Y_{\infty} \cup Y_{X}$と$g’:X_{Y} \rightarrow Y_{Y}$です。2.では、$f’$と$g’^{-1}$を使って$h$を構成しています。
残りの3.は、ただ確認するだけです。
従って、この主張の重要な点は証明部分の「単射$f,g$による集合の元を分類すること」と「$f,g$を制限することで全単射を構成すること」の2つだったわけです。
これにて、当初目標としていた定理が示されました。
次につながる話
さて、目標達成したので素朴集合論の前半は終了です。と言うことは後半が存在します。
それは、今回の証明で現れた「特定の元の集まりでキレイに分割する」ことです。これは、「類別」と言う部分集合による分割の一種です。ただの類別の場合は、共通部分が$\emptyset$とは限りませんが、今回のように互いに共通部分が$\emptyset$となるものはダブりなしでとても良い性質であると言えます。
そうした特別な類別の中で強力なものが「同値類」です。これは、分けるときの基準を同値関係によって定めるもので集合に構造を入れる場合に必ずセットで現れます。同値関係は、似たもの同士かどうかを判定できるものでした。つまり、同値類の元たちは同じものをみなすことで実質考える元を減らすことができるようになります。それが、「商集合」です。
また補足的に、可算・非可算を定義したために発生する添え字の書き方・考え方を導入します。つまり、共通部分や和集合を非可算なものでも問題ないことを考えていきます。また、可算個の集合でも無限個を共通部分などが考えられます。この場合と非可算のケースがほぼ同じように考えられることも見ていきます。
同値類はおそらく数学の基礎でもかなり重く、後半の話の大半はこれについてになるでしょう。それほど、理解せずに進むと立ちいかなくなる概念です。
商集合は構造あって初めて価値を感じられます。
後半の最終目標は「様々な例を見ていき同値類の価値を認識すること」だと言えます。
おわりに
八か月がけで続いてきた集合論ですが、実際は後半の話を合わせてもまだまだたくさんトピックがあります。このシリーズでは、一つの目標に向かって必要な知識を埋めていく形式なので一般の集合論の本や記事のように網羅的には書けませんでした。それでも、各定義ごとに納得がいく動機づけを心がけてきたため、少しでも定義の意味を納得できたなら幸いです。
それでは、後半の「類」と「類別」の話でまた。ケンけんでした。