こんにちは!ケンけんです。前回は、写像を一般の場合と直積集合での定義を見ました。
今回は、写像による同値関係を考えることで全単射を考えます。
キーワード:全単射
必要知識:同値関係
導入
写像の導入の時に、秀吉の木をひもで数え上げる逸話がありました。
例:一本の木と一本のひも(左)、二本の木と一本のひも(右)
その時は、ひも1本に対しての縛り方は木一本でも木2本でも問題ないとしました。でも、上の図の右側の数え上げは問題が発生することがあります。それは、紐に対して木が余ってしまった場合です。ひも一本に対して木2本を括り付けているなら、木の総数が奇数の場合木が一本だけ残りひもの括り付けるルールが破綻します。
そんなもの「$2 \times 使ったひもの本数+1$」で木の本数がわかるからいいじゃないと思いそうですが、これは写像ではありません。現実ならそのように対応できますが、数え上げ方がわからないことを前提に「ひもと木の本数を対応で木を数えよう」という突然無から$2$倍や足し算などの道具取り出しています。やはり、道具作りに例外を許してはいけません。この数え上げを作るためには例外を出さないひもと木の括り付けを考える必要があります。
その括り付け方が、逸話のひも1本と木1本です。この関係は、ひもから木の本数を数えることに目が活きますが、木の本数がわかっていれば使ったひもの本数もわかることを意味しています。つまり、数えるための道具と数えられる対象を置き換えても同じことが成立しています。
- 使ったひもの本数$\Rightarrow$生えている木の本数(逸話での考え方)
- 木の本数$\Rightarrow$使ったひもの本数!(逆の考え)
数え上げ以外の例として、ペアづくりを考えてみます。1つのクラスごとに生徒はそれぞれ出席番号があります。生徒数の同じ2つのクラスで、出席番号が同じ生徒同士でペアを作るようにします。
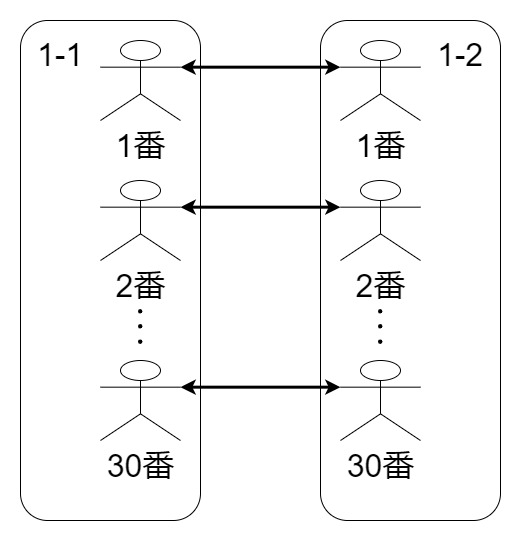
例:2つのクラス間の生徒のペアづくり
こうすることで、「1年1組番号〇〇の〇〇さん」を指定するとペアである1年2組の同じ番号の生徒が自然に決まります。逆に「1年2組番号○○の○○さん」を指定するとペアの1年1組の同じ番号の生徒がわかります。
このペアの作り方は、次の性質を持っています。
- 「$f:1年1組の生徒 \rightarrow 1年2組の生徒$」と「$g:1年2組の生徒 \rightarrow 1年1組の生徒$」は写像
- 2つの写像を合成すると元の生徒に戻る。「(生徒Aのペア)のペアは生徒A」
この2つの事実は、ひもと木を一本ずつ括り付ける場合も持つ性質です。特に、合成$f \circ g,g \circ f$は直積集合では$(x,x)$の形の元からなる集合となっています。このような写像は、何も変わらない写像として「恒等写像」と呼ばれます。掛け算での$1$のような働きを持つ写像です。また、上の2つの性質を持つ写像を「全単射」または「双射」と呼ばれます。
定義
それでは、定義していきます。
$U$:普遍集合 $X,Y \subset U$
$\mathrm{id}_{X}:X \rightarrow X(x \mapsto x)$:$X$の恒等写像($identity \; map$)
$f:X \rightarrow Y$:写像
$f$は双射($bijection$)$\overset{def}{\iff} \exists g:Y \rightarrow X((g \circ f=\mathrm{id}_{X}) \wedge (f \circ g=\mathrm{id}_{Y}))$
$f:X \rightarrow Y$が双射であるとき, $f:X \overset{\sim}{\rightarrow} Y$と書く.
$f$を双射とする写像$g$は「$f$の逆写像($inverse \; map$)」と呼び$g=f^{-1}$と書く.
$X$は$Y$と(集合として)同型$\overset{def}{\iff} \exists f:X \rightarrow Y(f:X \overset{\sim}{\rightarrow} Y)$
ほとんどの和書では、「全単射」と書かれています。が、英語の単語を見ると双射の方が正しいです。また、「双」と言う字から$X \rightarrow Y$と$Y \rightarrow X$の双方向で関係がある写像だと意味付けできたりします。ただし、日本語の記事なので今後はすべて全単射で統一します。
また写像ではなく集合の元に注目する場合は、「一対一対応(one-to-one)」と呼びます。証明の文章中で、いちいち写像を取りたくないと思っているのか、こちらで記述している書籍が意外と多いです。
同型は同値関係
この同型とは、数集合の構造が同じことを意味します。四則演算や近さなども構造です。導入にあった生徒ペアづくりから、集合として同型は2つの集合の元の数が同じであるように見えます。
普遍集合$U$の部分集合の中で同型の関係は次のような同値関係を作ることができます。
$$X \cong Y \overset{def}{\iff} \exists f:X \rightarrow Y(f:全単射)$$
$U$:普遍集合 $X,Y \subset U$
- 「$X \cong Y \overset{def}{\iff} \exists f:X \rightarrow Y(f:全単射)$」は同値関係である.
任意の$X,Y,Z \subset U$を取る.
反射律について$\mathrm{id}_{X}:X \rightarrow X$は自分自身が逆写像である.
従って,$X \cong X$である.
対称律について$X \cong Y$を仮定すると,全単射な$f:X \rightarrow Y$が存在する.
このとき,$f$の逆写像$g=f^{-1}:Y \rightarrow X$が存在する.
$g \circ f=\mathrm{id}_{X},f \circ g=\mathrm{id}_{Y}$より,$g$に対して逆写像$g^{-1}$は$f$である.
以上から,$g$は全単射であり$Y \cong X$である.
推移律について$X \cong Y, Y \cong Z$を仮定すると,全単射な$f:X \rightarrow Y, g:Y \rightarrow Z$が存在する.
このとき,$g \circ f:X \rightarrow Z$に対して写像の一致の確認により$(g \circ f) \circ (f^{-1} \circ g^{-1})=\mathrm{id}_{Z}, (f^{-1} \circ g^{-1}) \circ (g \circ f)= \mathrm{id}_{X}$である.
以上から, $g \circ f$は全単射であり$X \cong Z$である.
$\square$
実は、この先構造を含む集合間の同型も同様に示せたりします。簡単な同値関係の証明なので折りたたんでおきます。解いてみてください。
おわりに
今回のそうと同型は、数え上げから話が始まりましたが元が数えられない集合の間の個数を判断する材料になります。実際には、次回の単射(入射)が本題なのですが、数え上げの基本は今回の全単射に始まります。
次回は、全単射を崩した単射・全射を取り扱います。
以上、ケンけんでした。
同値関係についての記事

