こんにちは!ケンけんです。前回は、写像の合成を操作の分割によって考えました。
今回は写像の一致をよくある方法と直積集合を使った2通りで考えていきます。
そして、合成によって描かれる「可換図式」を取り上げます。
キーワード:可換図式
導入
前回では、$4$倍写像$m_{4}$が2倍写像$m_{2}$の合成であることを導入で挙げました。
$m_{2} \circ m_{2}$は整数を4倍する写像より$m_{4}=m_{2} \circ m_{2}$としたいところです。では、整数以外の具体的には書き下せない一般の集合ならどうでしょう。
これまで命題・述語を利用して集合の情報を作ってきた流れから、直積集合による写像の見方で写像が一致することを考えてみます。
まず、写像の述語部分を$n$倍写像用にします。
- $m_{2}=\{(x,y) \in \mathbb{Z} \times \mathbb{Z}|y=2x\}$
- $m_{4}=\{(x,y) \in \mathbb{Z} \times \mathbb{Z}|y=4x\}$
- $m_{2} \circ m_{2}=\{(x,z) \in \mathbb{Z} \times \mathbb{Z}|\exists ! y \in \mathbb{Z}((y=2x) \wedge (z=2y)\}$
写像の元$(x,y)$が満たす条件なので、既に変数が考えられており述語のみの表記でよくなっています。整数の計算は既に知っているため、述語の表記として使っても問題ありません。
そして、$m_{2} \circ m_{2}=m_{4}$が言えれば直積集合として一致するため、写像として一致すると言ってもよさそうです。
$(x,z) \in m_{2} \circ m_{2}$についてただ一つの$y \in \mathbb{Z}$が存在して$y=2x,z=2x$が成り立ちますが、整数の計算から$z=2(2x)=4x$となります。
$y,z$は一意的に存在しており$y$を無視して$x,z$だけで考えても$z$の一意性は崩れません。
従って、$(x,z) \in m_{4}$となり、$m_{2} \circ m_{2} \subset m_{4}$がわかりました。
逆の包含は、$z=4x=2(2x)$から$y=2x$が$(x,y) \in i_{2},(y,z) \in i_{2}$を満たしていることから成り立ちます。
以上から、言いたい集合の一致が言えたため、$m_{2} \circ m_{2}=m_{4}$です。
でもこれ、説明としては正しくてもいちいち直積集合と一意性を持ち出すのは面倒です。そこでももう一つの一般の手法が役立ちます。
それは、写像を$f:X \rightarrow Y(x \mapsto y)$の方法で見ることです。合成写像$g \circ f$でスポットが当たるのは、$f$の定義域と$g$の値域だけです。そして集合の元もこれらの直積集合です。よって、$x \in \mathbb{Z}$について$m_{4}(x)=(m_{2} \circ m_{2})(x)$が言えれば十分ではないかということです。実際、$n$倍写像ではこれがうまくいきます。
では一般の写像ではどうかと言われると少し怪しいです。そこで、一度直積集合の方に戻り一般のやり方での写像の定義を見てみます。一般の方法では、「対応させる規則」と言う怪しい言葉を使っていましたが、直積集合の方で色々考えた今なら説明できるはずです。
$U$:普遍集合 $X,Y \subset U$
$X$から$Y$への写像($mapping$):$X$の各元に対して、$Y$の元をひとつ対応させる規則
$f:X \rightarrow Y(x \mapsto y)$と書く。
$x \in X$について$y=f(x)$となる$y \in Y$を$x$の像($image$)
この$f(x)$は$x$に対してただ一つの$y$だから書くことができるのでした。このフレーズは、直積集合での写像の定義にありましたね。そして、well-definedを考えるときは次を調べればよかったです。
$$f:X \rightarrow Y , x,x’ \in Xについてx=x’ \Rightarrow f(x)=f(x’)$$
この述語部分はまさしく直積集合での写像の述語部分です。
写像の定義の段階でこの言いかえができますが、述語を追いかけるためにあえて封印していました。
直積集合での方法では、$m_{2} \circ m_{2}$と$m_{4}$の元が互いにもう一方の述語を満たすことで示しました。先ほどの直積集合の話で既に示した$m_{2} \circ m_{2}=m_{4}$から述語を書いて見ます。
$$\forall (x,y) \in m_{2} \circ m_{2}=m_{4}(x=x’ \Rightarrow m_{2} \circ m_{2}(x)=y=m_{4}(x))$$
これによって、$m_{2} \circ m_{2}(x)=m_{4}(x)$が言えています。以上から、同じ元$x$を写像で写して像が一致する場合に写像が一致すると言ってよいことになります。
この考えは、合成写像との一致だけでなく2つの写像が一致することにも利用できます。
定義 写像の一致
それでは、定義しますが直積集合のやり方からよくある手法を導いたので一般の書き方で定義してしまいます。
$U$:普遍集合 $X,Y \subset U$
$f:X \rightarrow Y,g:X \rightarrow Y$:写像
$f$と$g$は等しい$ \overset{def}{\iff} \forall x \in X(f(x)=g(x))$
$f=g$と書く。
この定義から、写像は区別できるため写像を特定の述語$P(x)$を満たすように集めたものは集合となります。$X$から$Y$への写像全体の集合を$\mathrm{Map}(X,Y)$と書きます。
可換図式
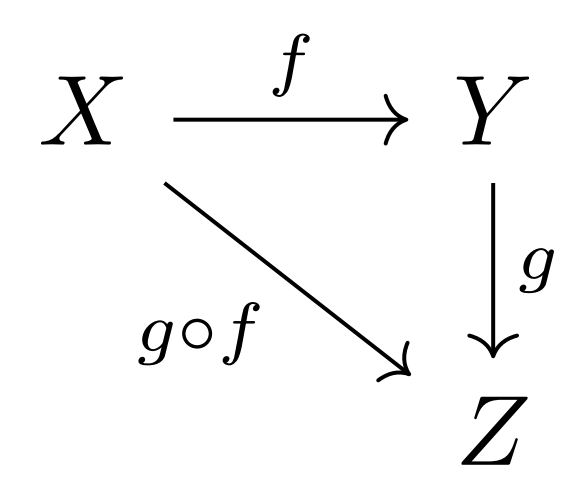
数学をやっていれば嫌でも上のような図を見たことが一度はあるはずです。$f$と$g$の矢印を経由する上のルートと$g \circ f$の矢印を経由することは、合成写像であることからすぐにわかります。つまり上ルートと下ルートで、写像としての結果が変わりません。
このような図式を「可換図式($commutative \; diagram$)」と呼びます。
上の図だと明らかすぎるので次の図も考えてみます。

この場合、上ルートと下ルートが一致するかがわからず可換図式とは限りません。なので、これが「可換図式だ!」と言うためには、$h=g \circ f$を示す必要があります。ここからも、合成写像の利用価値がわかるでしょう。
おわりに
今回は、直積集合が論理を追うと言う点ではよいのですが実際に確認するとなると、よくある写像の書き方に言い換えて説明した方がよいと言う好例でした。初めに議論するときは、直積集合を利用してきましたが徐々に一般の書き方に遷移していくと思います。
次回は、全単射こと「双射」と逆写像を取り扱います。
以上、ケンけんでした。

