こんにちは!ケンけんです。前回は、順序関係における上界下界について取り扱いました。
今回から、集合と必ずセットで語られる写像について取り扱います。
キーワード:写像
導入
この「写像」というワードは、とある事情で非数学科の方でも耳にしたことがあるのではと思います。しかし、実際にはどんなところで使われているのかを考えることはありません。せいぜい関数の一般化で議論が終わってしまうでしょう。なのでまずは、どんなところで使われてきたのかを見ていきます。
一番単純なケースは数え上げです。モノの数や個数の大小を四則演算を使わずに調べることができますか。そんなの無理と一瞬思いそうになりますが、実は算数の始めの始めに語られています。それは一対一対応を利用する方法です。
次の文章は算数科の学習指導要領からの引用です。
(ア)個数を比べること
ものの個数を比べる場合、それぞれの個数を数えなくても、1対1の対応をつけることで,個数の大小や相等を判断できる。
文部科学省 小学校学習指導要領(平成29年告示)解説 算数編 p79
つまり、数を知らなくてもものをひとつずつ組を作ることで大小を判定でき、一方が数えられるもの(数えやすいもの)を使うことでもう一方のものがどれくらいあるのかを直接調べなくても知ることができます。
日本人の逸話でもこの発想は登場します。豊臣秀吉の「木の本数を数える」エピソードです。
あるとき、秀吉は当時仕えていた織田信長に山の木の本数を数えるように命じられます。その時に使ったのは、本数がわかっている大量のひもを用意し、山の木に1本ずつ括り付け最終的に残ったひもの本数を用意していた本数から引くことで使用した本数(=山の木の本数)を判定したと言われています。
(でもよく大量のひもを準備段階で数えたな。)
また、別に1個ずつセットにしなくてもいいです。上の秀吉の例の場合、1本にひもを5本ずつくくることで、より少ないひもの準備で数え上げることができます。
例:一本の木と一本のひも(左)、二本の木と一本のひも(右)
これは組の作り方が違うだけで、発想は同じ2つのものを組にして対応を考える方法です。この組を作って対応を考えることが写像の基本思想です。
この2つのものを組にして考える発想が集合に存在しました。直積集合です。そのために、木とひもをそれぞれ区別して集合$X$を木の集合、$Y$をひもの集合とします。
このとき、任意の木$x \in X$にひも$y \in Y$をくくりつけて組を作ります。この時、一つの木に対してひもは一つしか使わないので、もし木を一つ選んだ場合、対応するひもはただ一つに決まります。従って、「対応する」を命題論理から定義しようとすると次のように考えれば十分そうです。
今、任意の対応させたいものの集合を$X$、対応先のものの集合を$Y$、「対応」を意味する集合として$S \subset X \times Y$と置きます。
$$任意のx \in Xについて(x,y) \in Sとなるy \in Yがただ一つ存在する$$
つまり$S$は次のように書かれます。
$$S=\{(x,y) \in X \times Y|\forall x \in X \exists ! y \in Y((x,y) \in S)\}$$
述語部分に集合が存在することは気持ち悪いので次のよう変数部分に移動して解決します。
$$S=\{(x,y) \in X \times Y|\forall (x,y), (x’,y’) \in S(x=x’ \Rightarrow y=y’)\}$$
こちらならば、述語部分が元のみで構成されて見やすいです。
このように、「わからないもの」を「わかるもの」と組にすることから情報を抜き取って言葉「対応する」を決めます。これが写像です。対応を示す道具なのです。
定義
それでは定義の段ですが2通りの定義を紹介します。まずは一般的な方です。
$U$:普遍集合 $X,Y \subset U$
$X$から$Y$への写像($mapping$):$X$の各元に対して、$Y$の元をひとつ対応させる規則
$f:X \rightarrow Y(x \mapsto y)$と書く。
$x \in X$について$y=f(x)$となる$y \in Y$を$x$の像($image$)
$X$:$f$の定義域($domain$)
$Y$:$f$の値域($range$)(または終域($codomain$))
こちらの場合は論理式で表現できないため言葉で書くことになります。なぜなら、規則も対応も言葉ではわかっても命題論理ではまだ作っていないからです。
ほとんどの集合論の書籍では、「集合の元をもう一つの集合の元への対応」だとか「集合の元をもう一つの集合の元へ対応させる規則」と説明されます。しかし、これまで命題論理ですべて構成してきたのだから、導入で考えた直積集合の特殊なものとしてみなすことで説明する方が筋が通るでしょう。
$U$:普遍集合 $X,Y \subset U$
$f =\{(x,y) \in X \times Y|\forall (x,y), (x’,y’) \in f(x=x’ \Rightarrow y=y’)\}$
$f$:$X$から$Y$への写像($mapping$)
$X$から$Y$への写像$f$は$f:X \rightarrow Y(x \mapsto y)$と表現する。
$x \in X$について$(x,y) \in f$となる$y \in Y$を$x$の像($image$)と呼ぶ。
このとき、$f(x)=y$と書く。
$X$:$f$の定義域($domain$)
$Y$:$f$の値域($range$)(または終域($codomain$))
この方法ならば、今までの言葉(命題論理・集合)だけで説明できます。またどちらも意味としては同じことになります。1つ目の方法を採用する書籍では、2つ目の方法を別の定義として持ってきます。
それがグラフです。
$U$:普遍集合 $X,Y \subset U$
$f:X \rightarrow Y$:写像
$G(f)=\{(x,f(x)) |x \in X\} \subset X \times Y$:$f$のグラフ($graph$)
じっくり見比べると2つ目の定義と同じことを書いているとわかるでしょう。このグラフは高校までの関数のグラフそのものです。写像が関数の一般化だとは、導入で触れましたが直接例を見てみましょう。
関数$f:\mathbb{R} \rightarrow \mathbb{R}(x \mapsto 2x+1)$
$f=\{(x,y) \in \mathbb{R}^2|y=f(x)=2x+1\}$が関数$f$を表す。
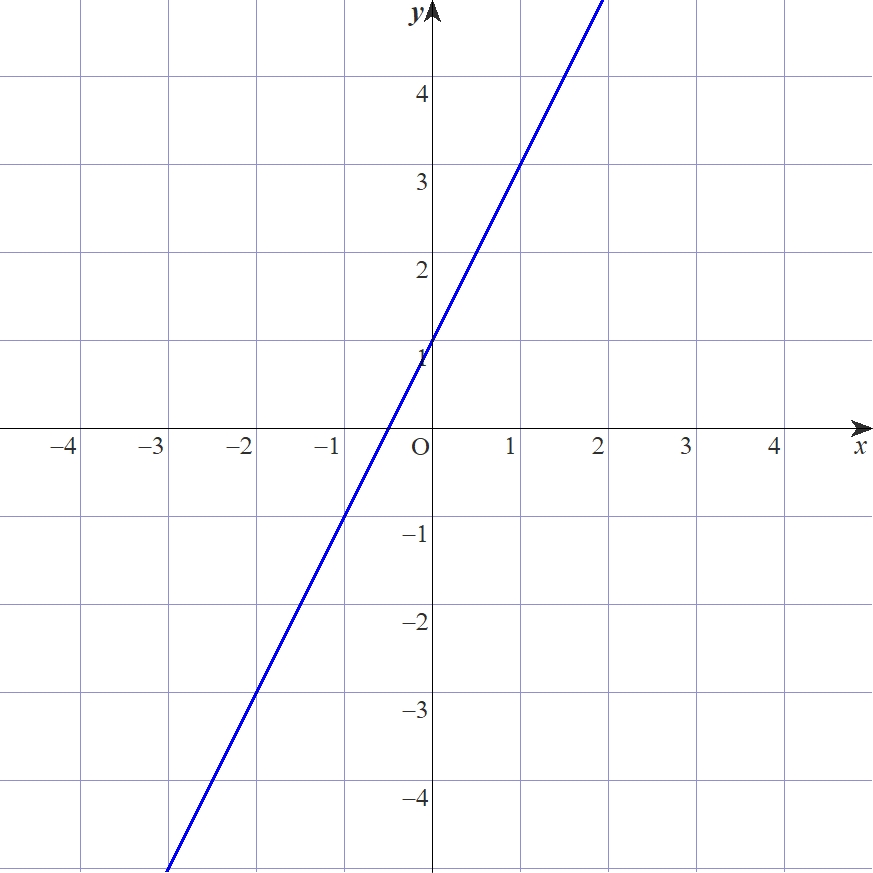
例:$f(x)=2x+1$のグラフ
この例より直線のグラフは、関係$f$を満たす座標平面上の点の集合であり、$\mathbb{R} \times \mathbb{R}$の部分集合であるとわかります。この説明があるために、写像は関数の一般化との話に説得力が出るでしょう。
忘れたときにやってくるwell-defined
ここまで写像の見方と定義を考えてきましたが、実はよく見落とされる点があります。$f:X \rightarrow Y$について任意の$x \in X$に対して$(x,y) \in f$とする$y \in Y$がただ一つであることです。
一つ目の定義を主にする本ではここをあまり重要視してないのか、さも当然のように$f(x)=y$と$f(x)$を使っています。しかし本来は無関係のはずの$y$を$f(x)$と書いてよいのはなぜでしょう。それは、$x$に対して$y$がただ一つに決まるため、$y’ \neq y$とする$y’ \in Y$について$$(x,y’) \notin f$$であるからです。つまり、$(x,y) \in f$となる$y$を「$x$に従う$Y$」の元という意味を込めて$f(x)$と書いても問題ないのです。$x$が独立変数と呼ぶならば、$y$が従属変数だと言うのも納得でしょう。
写像$f:X \rightarrow Y$が正しく定義されていることを、「$f$は$well$-$defined$である。」と呼ばれます。これは一意性の確認です。その確認としては、次の命題が真であることを確かめれば十分です。$$\forall x ,x’ \in X(x=x’ \Rightarrow f(x)=f(x’))$$集合の元は具体的でない場合は一般に一致するとは限りません。しかし、数では同じものでも違う表記をすることができます。例えば、$$1= \frac{2}{2}= \frac{5}{5} = \ldots$$はすべて計算すると1ですが、有理数の元の表示としては違います。
このとき、次のような写像らしきものを考えてみます。
$$f:\mathbb{Q} \rightarrow \mathbb{Q} ( x \mapsto \begin{cases} x & \text{($x$の分母は1)} \\ 2x & \text{(それ以外)} \end{cases} )$$
これは写像ではありません。なぜなら、$1= \frac{2}{2}$について$f(1)=1$ですが、$f(\frac{2}{2})=2 \times \frac{2}{2}=2$より$f(1)\neq f(\frac{2}{2})$です。しかし、書き方が違うだけで$1= \frac{2}{2}$より$f(1)= f(\frac{2}{2})$になる必要があります。よって、一意的に$f(x)$が定まらないので写像ではありません。
このように、対応をなんでも勝手に作ってよいのではなく表示に関わらずにただ一つの元と組になるように対応を作らなければ写像と呼んではいけないです。
今後の数学で適当な写像を作ったりする場合は必ず付いて回ります。何か対応を考えるときは、定義した後に必ず$well$-$defined$か確認するようにするとミスが少なくて済みます。
おわりに
$well$-$defined$は、代数系を本格的に学び始めると登場する準同型写像の構成で現れます。また、四則演算もある種の写像なので新しく作った場合には確認する必要が出てきます。ひどい場合だと、ほとんど当たり前だと思っていた対応も全然あたりまえでなく、説明が途方もないほど大変なものもあります。まず、高校までの関数がすべて写像であることを確認することから練習してなれるといいと思います。中には、調べるのが大変な関数もありますし。
(余談ですが秀吉の例、ネットの記事はあるのですが一次ソースを見つけられませんでした。昔算数辞典のようなもので見かけたので、逸話のようなものなのでしょうか。曽呂利新左衛門との米のエピソードは見つかったのですが。)
次回は、全単射を取り扱います。
以上、ケンけんでした。
参考文献
写像の直積集合による定義から話している本
齋藤正彦,2002,数学の基礎 集合・数・位相,東京大学出版会
今回引用した学習指導要領
文部科学省,2017,小学校学習指導要領(平成29年告示)解説 算数編,文部科学省

